Suites numériques, bac S 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. ...... .....   Métropole. On considère la fonction f définie sur R par : f (x) =0,5 x2 -x +1,5 Soit a un réel positif. On définit la suite (un) par u0 = a et, pour tout entier naturel n : un+1 = f (un). Le but de cet exercice est d’étudier le comportement de la suite (un) lorsque n tend vers +∞, suivant différentes valeurs de son premier terme u0 = a. 1. À l’aide de la calculatrice, conjecturer le comportement de la suite (un) lorsque n tend vers +∞, pour a = 2,9 puis pour a = 3,1. Si u0 = 2,9 la suite tend vers 1. Si u0 = 3,1 la suite tend vers plus l'infini. 2. Dans cette question, on suppose que la suite (un) converge vers un réel ℓ. a. En remarquant que un+1 =0,5un2-un+1,5 ,montrer que ℓ =0,5ℓ 2-ℓ+1,5. La suite converge vers l  et la fonction f(x) est continue en l. un+1 = f(un) tend vers l quand n tend vers plus l'infini. D'autre part un+1 tend vers l quand n tend vers plus l'infini. Par passage à la limite : l = f(l). b. Montrer que les valeurs possibles de ℓ sont 1 et 3. 0,5ℓ 2-2ℓ+1,5 =0 ; D = 4 -4 x 0,5 x1,5 = 1. Solutions : (2 ±1) / 1 = 2 ±1 soit 1 et 3. 3. Dans cette question, on prend a = 2,9. a. Montrer que f est croissante sur l’intervalle [1 ; +∞[. f '(x) = x-1. f '(x) est positive sur [1 ; +∞[. Donc f(x) est croissante sur cet intervalle. b. Montrer par récurrence que, pour tout entier naturel n, on a : 1 < un+1 < un. Initialisation : u0 = 2,9 ; u1 = 2,805, la propriété est vraie au rang 1. Hérédité : on suppose que la propriété est vraie au rang n. 1 < un+1 < un. La fonction f étant croissante sur [1 ; +∞[, un et un+1 appartiennent à cet intervalle donc f(un) > f(un+1), c'est à dire un+1 > un+2. La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier n. c. Montrer que (un) converge et déterminer sa limite. La suite est décroissante et bornée, donc elle converge. La limite de la suite est l = 1. 4. Dans cette question, on prend a = 3,1 et on admet que la suite (un) est croissante. a. À l’aide des questions précédentes montrer que la suite (un) n’est pas majorée. Hypothèse : la suite est majorée par M signifie qu'elle converge vers 1 ou vers 3. Or u0 > 3. La suite étant croissante, elle ne peut pas converger vers 1 ou 3. L'hypoyhèse est donc fausse. La suite n'est pas majorée. b. En déduire le comportement de la suite (un) lorsque n tend vers +∞. Quand n tend vers plus l'infini, une suite croissante non majorée tend vers plus l'infini. c. L’algorithme suivant calcule le plus petit rang p pour lequel up > 106. Recopier et compléter cet algorithme. P est un nombre entier et U est un nombre réel. P <--- 0 U <---3,1 Tant que   U < 106 P <---P+1 U <---0,5 xU2 -U +1,5 Fin de Tant que. Liban. On considère pour tout entier n >0 les fonctions fn définies sur l'intervalle [1 ; 5 ) par : fn(x) = ln(x) / xn. On note Cn leurs courbes représentatives. 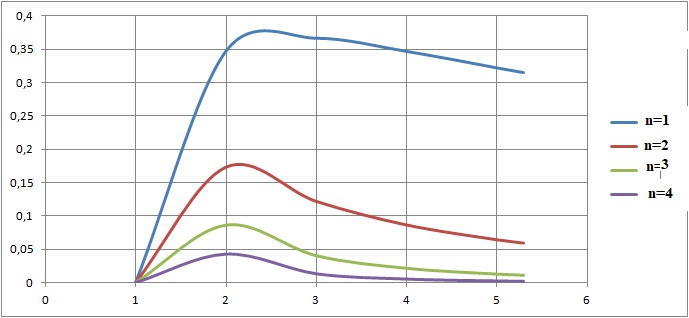1. Montrer que pour tout entier n >0 et tout x réel de l'intervalle [1 ; 5 ], fn'(x) = (1-n ln(x) )/ xn+1. On pose u = ln(x) et v = xn ; u' = 1 / x ; v' = n xn-1. (u'v-v'u) / v2 =( xn-1 - n xn-1ln(x) ) /  x2n = (1-n ln(x) )/ xn+1. 2. Pour tout n >0, on admet que la fonction fn admet un maximum sur l'intervalle [1 ; 5 ]. On note An le point de la courbe Cn ayant pour ordonnée ce maximum. Montrer que tous les points An appartiennent à une même courbe G d'équation : y = ln(x) / e. La dérivée s'annule pour ln(x) = 1 / n soit x = e1/n. Ordonnée de An : y = ln(e1/n) / e =ln(x) / e. 3.a. Montrer que pour tout entier n >1 et tout réel de [1 ; 5] : 0 < ln(x) / xn < ln(5) / xn. ln(1) = 0 ; ln(5) positif. La fonction logaritme est strictement croissante sur [1 ; 5 ]. 0 < ln(x) < ln(5).  xn est >1 sur [1 ; 5]. 0 < ln(x) / xn < ln(5) / xn. 3.b. 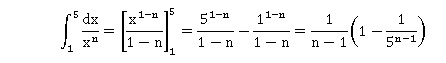Montrer que pour tout entier n >1 : c. Pour tout entier n >0, on s'intéresse à l'aire sous la courbe Cn, c'est à dire l'aire du domaine plan délimitée par la courbe Cn et les droites d'équation x=1 et x = 5 et y = 0. Déterminer la valeur limite de cette aire quand n tend vers plus l'infini. La fonction fn étant le quotient de deux fonctions positives sur [1 ; 5 ], pour n >0,  fn est positive. L'aire cherchée est : 1 / (n-1) [ 1-1 /(5n-1]. Quand n tend vers plus l'infini : 5n-1 tend vers zéro ; 1 / (n-1) tend vers zéro ; donc cette aire tend vers zéro. ... Amérique du nord. Un scooter radiocommandé se déplace en ligne droite à la vitesse constante de 1 m /s. Il est poursuivit par un chien qui se déplace à la même vitesse.. On représente la situation vue de dessus dans un repère orthonormé du plan d'unité 1 m. L'origine de ce repère est la position initiale du chien. Le scooter est représenté par un point appartenant à la droite d'équation x = 5. Il se déplace sur cette droite dans le sens des ordonnées croissantes. On étudie deux modélisations différentes de la trajectoire du chien. Partie A. Modélisation à l'aide d'une suite. A l'instant initial le scooter est représenté par le point S0 et le chien par le point M0. On considère qu'à chaque seconde le chien s'oriente instantanément en direction du scooter et se déplace en ligne droite sur une distance de 1 m. Ainsi à l'insatnt initial, le chien s'oriente en direction de S0, et une seconde plus tard, il se retrouve en M1. Le chien s'oriente en direction de S1 et se déplace en ligne droite de 1 m et ainsi de suite. On modélise les trajectoires du chien et du scooter par deux suites de points notés (Mn) et (Sn). Au bout de n secondes, les coordonnées du point Sn sont ( 5 ; n). On note (xn ; yn) les coordonnées du point Mn.   1. Construire sur le graphique les points M2 et M3. 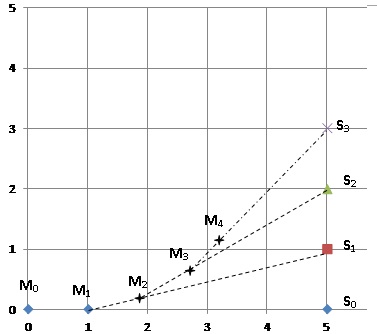2. On note dn la distance entre le chien et le scooter n secondes après le début de la poursuite. dn = MnSn. Calculer d0 et d1. d0 =M0S0= 5 ; d1 =M1S1= (12 +42)½ =17½ . 3. Justifier que le point M2 a pour coordonnées ( 1 + 4 / 17½ ; 1 / 17½). Equation de la droite S1M1 : y = a x +b. S1(5 ; 1 ) appartient à cette droite :1 = 5a +b. M1(1 ; 0 ) appartient à cette droite :0 = a +b soit b = -a. Par suite a = 0,25 et b = -0,25. y = 0,25 x -0,25. Les coordonnées de M2 vérifient-elle cette équation ? 1 / 17½ =0,25 +1 / 17½ -0,25 ; cette égalité est vérifiée. Les coordonnées de M2 vérifient l' équation de la droite (S1M1) : M2 appartient à cette droite. Vérifions que M1M2 = 1 ; M1M2 2=(1 + 4 / 17½ -1)2 +; 1 / 17 = 16 / 17 + 1 / 17 = 1. Le point M2 a bien  pour coordonnées ( 1 + 4 / 17½ ; 1 / 17½). 4. On admet que pour tout entier naturel n : xn+1 = xn +(5-xn) / dn ; yn+1 = yn +(n-yn) / dn ; a. le atableau ci-dessous, obtenu à l'aide d'un tableur donne les coordonnées des points Mn et Sn ainsi que la distance dn en fonction de n. Quelles formules doit-on écrire dans les cellules C5 et F5 et recopier vers le bas pour remplir les colonnes C et F ? 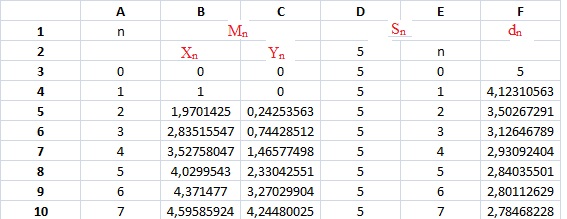En F5 : =RACINE((5-B5)^2+(E5-C5)^2)) En C5 : =C4+(A4-B4)/F4 b. On admet que la suite (dn) est strictement décroissante. Justifier que cette suite est convergente et conjecturer de sa limite. Cette suite est strictement décroissante et minorée par la distance zéro ( une distance est positive ). Donc elle converge. D'après le tableau, sa limite est 2,77. Antilles. Le directeur d’une réserve marine a recensé 3 000 cétacés dans cette réserve au 1er juin 2017. Il est inquiet car il sait que le classement de la zone en « réserve marine » ne sera pas reconduit si le nombre de cétacés de cette réserve devient inférieur à 2 000. Une étude lui permet d’élaborer un modèle selon lequel, chaque année : • entre le 1er juin et le 31 octobre, 80 cétacés arrivent dans la réserve marine ; • entre le 1er novembre et le 31 mai, la réserve subit une baisse de 5% de son effectif par rapport à celui du 31 octobre qui précède. On modélise l’évolution du nombre de cétacés par une suite (un). Selon ce modèle, pour tout entier naturel n, un désigne le nombre de cétacés au 1er juin de l’année 2017+n. On a donc u0 = 3000. 1. Justifier que u1 = 2926. u1 = (u0 +80) x0,95 =2926. 2. Justifier que, pour tout entier naturel n, un+1 = 0,95un +76. un+1 = 0,95( un +80) = 0,95un +76. 3. À l’aide d’un tableur, on a calculé les 8 premiers termes de la suite (un ). Le directeur a configuré le format des cellules pour que ne soient affichés que des nombres arrondis à l’unité. A B C D E F G H I 1 n 0 1 2 3 4 5 6 7 2 un 3000 2926 2856 2789 2725 2665 2608 2553 Quelle formule peut-on entrer dans la cellule C2 afin d’obtenir, par recopie vers la droite, les termes de la suite (un) ? =0,95*B2+76 4. a. Démontrer que, pour tout entier naturel n, un >1520. Initialisation : u0 > 1520, la propriété est vraie au rang zéro. Hérédité : on suppose la propriété vraie au rang n : un >1520. 0,95 un > 0,95 x1520 ; 0,95  un >1444. 0,95  un +76 >1444 +76 ; un+1 > 1444 +76. un+1 > 1520. Conclusion. la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel. b. Démontrer que la suite (un) est décroissante. un+1 -un = 0,95un +76 -un =76 -0,05 un. un >1520 ; 0,05un >1520 x0,05 ; 0,05un >76. un+1 -un < 0 ; un+1  < un ; la suite est décroissante. c. Justifier que la suite (un) est convergente. On ne cherchera pas ici la valeur de la limite. La suite est décroissante  et minorée, elle est donc convergente. 5. On désigne par (vn) la suite définie par, pour tout entier naturel n, vn = un −1520. a. Démontrer que la suite (vn) est une suite géométrique de raison 0,95 dont on précisera le premier terme. vn+1 = un+1 −1520. vn+1 =0,95un +76-1520. vn+1 =un -0,05 un +76-1520. vn+1 =un -1520 -0,05 un +76. vn+1 =vn  -0,05( un +1520). vn+1 =vn  -0,05 vn =0,95 vn. Il s'agit donc d'une suite géométrique de raison égale à 0,95 et de premier terme : v0 = u0-1520 = 3000-1520 = 1480. b. En déduire que, pour tout entier naturel n, un = 1480×0,95n +1520. vn = 1480 x 0,95n = un −1520. un = 1480×0,95n +1520. c. Déterminer la limite de la suite (un). 0 < 0,95 <1, donc 0,95 n tend vers zéro si n tend vers plus l'infini. La limite de la suite (un) est égale à 1520. 6. Recopier et compléter l’algorithme suivant pour déterminer l’année à partir de laquelle le nombre de cétacés présents dans la réserve marine sera inférieur à 2 000. n←0 u←3000 Tant que u > 2000 n←n+1 u← 0,95 *u +0,76. Fin de Tant que La notation «←» correspond à une affectation de valeur, ainsi « n ←0 » signifie « Affecter à n la valeur 0 ». 7. La réserve marine fermera-t-elle un jour ? Si oui, déterminer l’année de la fermeture. un = 1480×0,95n +1520 < 2000. 0,95n < (2000-1520) / 1480. n ln(0,95) < ln [(2000-1520) / 1480].  n > ln [(2000-1520) / 1480] / ln(0,95).  n >21,95. La réserve fermera l'année 2017 +22 soit en 2039. .... Amérique du sud. Soit k un réel strictement positif. On considère la suite (un) définie par u0 = 1, u1 = k et, pour tout entier naturel n par : un+2 =u2n+1 / (kun). On admet que tous les termes de la suite (un) existent et sont strictement positifs. 1. Exprimer u2, u3 et u4 en fonction de k. u 2=u21 / (ku0) = k. u 3=u22 / (ku1) = 1. u 4=u23 / (ku2) = 1 /k2. 2. À l’aide d’un tableur, on a calculé les premiers termes de la suite (un) pour deux valeurs de k. La valeur du réel k est entrée dans la cellule E2. 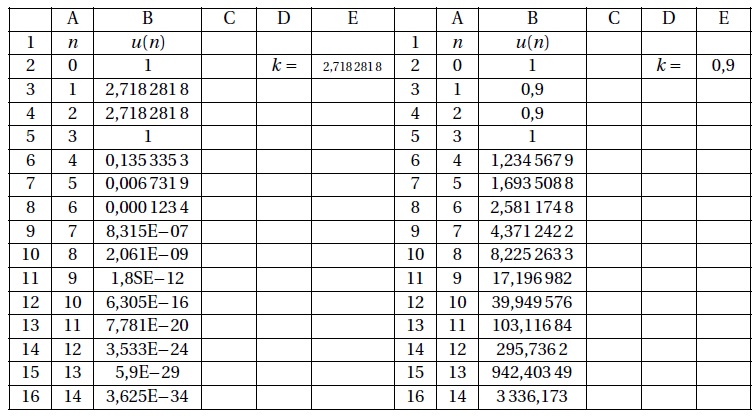a. Quelle formule, saisie dans la cellule B4, permet par recopie vers le bas de calculer tousles termes de la suite (un) ? =B3*B3/($E$2*B2) b. Conjecturer, dans chaque cas, la limite de la suite (un). Si k = 2,7182818, la suite tend vers zéro. Si k = 0,9, la suite tend vers plus l'infini. Dans la suite, on suppose que k =e. On a donc u0 = 1,u1 = e et, pour tout entier naturel n : un+2=u2n+1 / (e un).. 3. On définit, pour tout entier naturel n, la suite (vn) par : vn = ln(un+1)−ln(un). a. Démontrer que la suite (vn) est arithmétique de raison −1 et de premier terme v0 = 1. vn+1 = ln(un+2 / un+1) = ln(un+1/(eun) =ln(un+1) -ln(un) -ln(e) = vn-1. Il s'agit donc d'une suite arithmétique de raison -1. v0 = ln(u1)-ln(u0) = ln(e) -ln(1) = 1. b. En déduire, pour tout entier naturel n,l’expression de vn en fonction de n. vn = v0 +(-1)n = 1-n. 4. On définit, pour tout entier naturel n non nul la suite (Sn) par Sn = v0 +v1+· · ·+vn−1. a. Démontrer que, pour tout entier naturel n non nul, on a Sn =n(3−n) / 2 .Sn =1 +(1-1) +(1-2) +.... +(1-(n-1) = n x1 -(1+2+3+n-1) = n -n(n-1) /2 =n(3-n) / 2. ou bien Sn = n (v0 +vn-1) / 2 = n(1+1-(n-1) / 2 = n(3-n) / 2. b. Démontrer que, pour tout entier naturel n non nul, on a Sn = ln(un). Sn =ln(u1)-ln(u0) + ln(u2)-ln(u1) + ...+ln(un)-ln(un-1) = -ln(u0 + ln(un) = -ln(1) +ln(un) = ln(un). 5. a. Exprimer un en fonction de n et en déduire la limite de la suite (un). ln(un) =n(3-n) / 2 ; un = exp[n(3-n) / 2]. b. Trouver la plus petite valeur de n telle que un < 10−50 par la méthode de votre choix (écriture d’un algorithme, résolution d’inéquation, etc.). exp[n(3-n) / 2] < 10-50 ; n(3-n) < 2 ln(10-50) ; -n2+3n - 2 ln(10-50) < 0 ; On cherche les racines de l'équation : n2-3n + 2 ln(10-50) =0. n2-3n -230,26 ~0 ; D = 9+4 x230,26 ~930,0 ; D½ ~30,5 ; n1 =(3 +30,5) / 2 ~ 16,75 et n2 =(3 -30,5) /  = -13,75. -n2+3n - 2 ln(10-50) < 0 pour n > 17. Avec un algorithme : A <-- 1 ; B <-- e ; N <-- 0 Tant que B > 10-50 C <-- B B <-- B2 / (A) A <-- C N <--N+1 Fin Tant que Afficher N+1.   .

menu