Fonctions
logarithme et exponentielle, bac S 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
......
.....
|
Métropole.
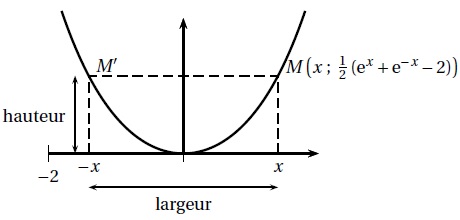
On a représenté ci-dessous la courbe d'équation y = 0,5 (ex+e-x-2).
On définit la "largeur" et la "hauteur" de l'arc de chaînette
délimité par les points M et M".
Le
but de cet exercice est d'étudier les positions possibles sur la courbe
du point M' d'abscisse x strictement positive afin que la largeur de
l'arc soit égale à sa hauteur.
1. Justifier que ce problème se
ramène à la recherche des solutions strictement positives de l'équation
(E) : ex+e-x-4x-2=0.
La hauteur est égale à y =0,5 (ex+e-x-2)
et la largeur est égale à 2x.
0,5 (ex+e-x-2)
= 2x soit ex+e-x-4x-2=0.
2. On note f la fonction définie sur
[0 ; +oo[ par f(x) = ex+e-x-4x-2.
2.a. Vérifier que
pour tout x >0, f(x) = x(ex / x-4) +e-x-2.
f(x) = x ex
/ x - 4x +e-x-2 = ex-4x+e-x-2
2.b. Déterminer la limite de f(x)
quand x tend vers l'infini.
Quand x tend vers plus l'infini :
e-x tend vers zéro.
x(ex
/ x-4) tend vers plus l'infini.
Par somme de limite f(x) tend vers plus l'infini.
3.a. Calculer f '(x), fonction
dérivée de f(x).
f '(x) = ex-e-x-4.
3.b. Montrer que f
'(x) =0 équivaut à : (ex)2-4ex-1=0.
ex(ex-e-x-4)
=0 ; (ex)2 -1 -4ex=0.
3.c. On pose X = ex.
Montrer que f '((x) = 0 admet une unique solution réelle ln(2+5½).
X2 -4X-1 = 0 ; déterminant D = 16+4 = 20.
On ne retient que la solution positive car ex >0 : X =
(4+20½) / 2 = 2 +5½ ; x = ln X = ln(2+5½).
4. On donne le tableau de signes de
la fonction f '(x).

4.a. Dresser le
tableau de variation de la fonction f.
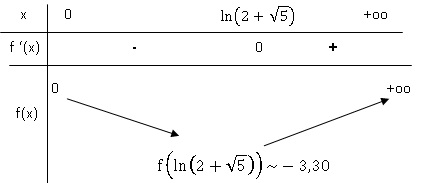
4.b. Démontrer que
l'équation f(x) = 0 admet une unique solution strictement positive
notée a.
Sur [0 ; ln(2+ 5½)], f(x) est négative donc f(x) = 0 n'a pas
de solution.
Sur [ ln(2+
5½) ; +oo[, f(x) est continue est strictement croissante ;
de plus la valeur zéro appartient à [f( ln(2+ 5½))
; +oo[ donc
d'après le corollaire du théorème des valeurs intermédiaires,
l'équation admet une solution unique.
5. On considère l'algorithme suivant
où les variables a, b et m sont réelles.
Tant que b-a >0,1 faire :
m <-- (a+b) / 2
Si em +e-m-4m-2 >0, alors
b <--m
Sinon : a <-- m
Fin Si
Fin tant que.
a. Les valeurs
initiales de a et b sont respectivement 2 et 3. Que contiennent-elles à
la fin de l'exécution de l'algotithme ? Justifier en complétant le
tableau suivant.
m
|
a
|
b
|
b-a
|
f(m)
|
|
2
|
3
|
1
|
|
2,5
|
2
|
2,5
|
0,5 > 0,1
|
~ 0,264 > 0
|
2,25
|
2
|
2,5
|
0,5 > 0,1
|
~ -1,4 < 0
|
2,375
|
2,25
|
2,5
|
0,75 > 0,1
|
~ -0,66 < 0
|
2,4375
|
2,375
|
2,5
|
0,125
> 1
|
~
-0,218 < 0
|
2,46875
|
2,4375
|
2,5
|
0,0625
< 0,1
|
|
On obtient
un encadrement de a
: 2,4375 < a
< 2,5.
6. La Gateway Arch
a l'allure ci-contre 
Son profil peut être approché par un arc de chaînette renversé dont la
largeur est égale à la hauteur.
La largeur de cet arc ( exprimée en mètre ) est égale au double
de la solution strictement positive de l'équation :
(E') :et/39 +e-t / 39 -4t /39 -2 = 0.
Donner un encadrement de la hauteur de la Gateway Arch.
t = 39a ; 2t = 78 a.
78 x2,4375 < hauteur < 2,5 x78 ; 190 < hauteur < 195.
Centres étrangers.
On se propose de tester un prototype de hotte aspirante.
A l'instant t = 0, la hotte est mise en marche et fonctionne
pendant 20 minutes. Les mesures permettent de modéliser le taux de CO2 ( en %) contenu dans le local au bout de t minutes de fonctionnement de la hotte par la fonction f définie sur [0 ; 20 ] par :
f(t) =(0,8 t +0,2)e-0,5t +0,03.
On donne le tableau de variation de cette fonction.
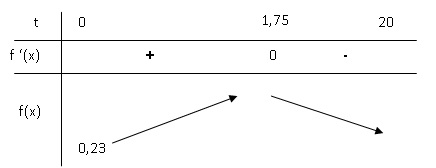
1.a. Calculer f(20).
f(20) = (0,8 x20 +0,2)e-10 +0,03 = 0,0307 ~0,031.
1.b. Déterminer le taux maximal de CO2 présent dans le local.
f(1,75) = (0,8 x1,75 +0,2) e-0,875 +0,03 = 0,697.
2. On souhaite que le taux de CO2 dans le local retrouve une valeur V < 3,5 %.
a. Justifier qu'il existe un unique instant T satisfaisant à cette condition.
f(0 ) = 0,23 ( 23 %) ; f(1,75) = 0,697 ( 69,7 %) ; sur [0 ; 1,75), f(t) est strictement croissante.
T n'appartient pas à cet intervalle.
f(1,75) = 0,697 ( 69,7 %) ; f(20) = 0,031 ( 3,1 %) ; sur [1,75 ; 20), f(t) est strictement décroissante.
T appartient à cet intervalle.
D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(t) = 0,035 admet une unique solution sur [0 ; 20 ].
b. On considère l'algorithme suivant :
t <-- 1,75
p <--0,1
V <--0,7
Tant que V >0,035
t <-- t+p
V <-- (0,8t+0,2)e-0,5t+0,03
Fin Tant que
Quelle est la valeur de t à la fin de l'algorithme ? Que représente cette valeur dans ce contexte ?
La calculatrice donne f(15,65) =0,0351, supérieure à 0,035 et f(15,75) =0,03486, inférieur à 0,035.
L'algorithme donne t = 15,75 minutes ou 15 min 45 s.
Au bout de 15 min 45 s, le taux de CO2 est inférieur à 3,5 %.
3. On désigne par Vm le taux moyen de CO2 présent dans le local pendant les 11 premières minutes de fonctionnement de la hotte.
a. Soit F la fonction définie sur [0 ; 11 ) par F(t) = (-1,6 t -3,6)e-0,5t +0,03t.
Montrer que F est une primitive de f(t) sur [0 ; 11].
Dériver F en posant u = -1,6t-3,6 et v = e-0,5t ; u' = -1,6 ; v' = -0,5 e-0,5t.
u'v + v'u = -1,6 e-0,5t +0,5(1,6t+3,6)e-0,5t = (-0,8t +0,2)e-0,5t.
F ' = (-0,8t +0,2)e-0,5t +0,03 = f(t).
b. En déduire Vm.
F(11) = (-1,6 x11 -3,6)e-5,5 +0,03x11=0,2434 ; F(0) = -3,6.
Vm = (F(11)-F(0)) / 11 =(0,2434+3,6) / 11 = 0,3484 ( 34,9 %).
|
...
|
|
Antilles.
Un publicitaire souhaite imprimer le logo ci-dessous sur un T-shirt :
Il dessine ce logo à l’aide des courbes de deux fonctions f et g définies sur R par :
f (x) = e−x (−cosx +sinx +1) et g (x)= −e−x cosx.
On admet que les fonctions f et g sont dérivables sur R.
Partie A. Étude de la fonction f.
1. Justifier que, pour tout x appartenant à R :
−e−x < f (x) < 3e−x .
-1 < cos x < 1 et -1 < sin x < 1.
-1-1+1 < -cos x + sin x+1 <1 +1 +1.
En multipliantmembre à membre par e-x >0 : −e−x < f (x) < 3e−x .
2. En déduire la limite de f en +oo.
Quand x tend vers plus l'infini : −e−x et 3e−x tendent vers zéro.
Le théorème des gendarmes conduit à : f(x) tend vers zéro quand x tend vers plus l'infini.
3. Démontrer que, pour tout x réel, f ′(x) = e−x (2cos x −1) où f ′ est la fonction dérivée de f .
On pose : u = e-x et v = -cos x + sin x +1 ; u' = -e-x ; v' = sin x + cos x.
u'v + v'u = -e-x (sin x + -cos x +1)+ e-x (sin x + cos x).
f ' (x) = e−x (2cos x −1)
4. Dans cette question, on étudie la fonction f sur l’intervalle [−p ; p].
a. Déterminer le signe de f ′(x) pour x appartenant à l’intervalle [−p ; p].
e−x est strictement positif ; 2 cos x -1 s'annule pour x = ± p/3.
2 cos x -1 est négatif sur [−p ; -p/3] et sur [p/3 ; p]
2 cos x -1 est positif sur [−p/3 ; p/3].
b. En déduire les variations de f sur [−p ; p].
Sur [−p ; -p/3] et sur [p/3 ; p], f(x) est strictement décroissante.
Sur [−p/3 ; p/3] f(x) est strictement croissante.
f(x) présente un minimum en -p/3 et un maximum en p/3.
Partie B. Aire du logo.
On note Cf et Cg les représentations graphiques des fonctions f et g dans un repère orthonormé
L’unité graphique est de 2 centimètres. Ces deux courbes sont tracées.
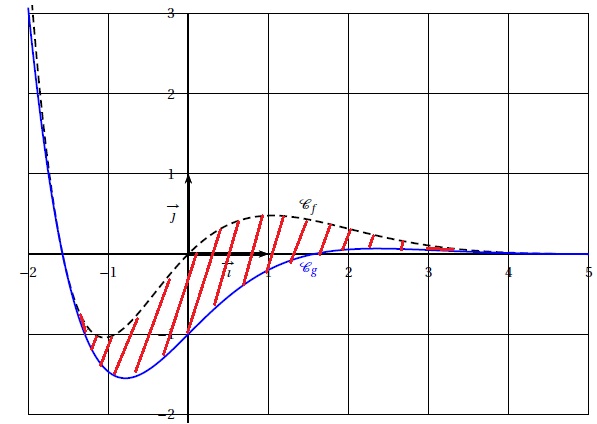
1. Étudier la position relative dela courbe Cf par rapport à la courbre Cg sur R.
f (x) -g(x) = e−x (−cosx +sinx +1) +e−x cosx = e−x ( sinx +1).
-1 < sin x < 1 ; -1 +1 < sin x + 1 < 1 +1 ; 0 < sin x + 1 < 2 ;
de plus e-x est strictement positif.
f (x) -g(x) > 0, donc Cf est au dessus de Cg.
2. Soit H la fonction définie sur R par :
H(x) = -0,5 ( cos x+ sin x+2)e-x.
On admet que H est une primitive de la fonction (sinx +1)e−x sur R.
On note D le domaine délimité par la courbe Cf , la courbe Cg est les droites d’équation x = -0,5p et 1,5 p.
a. Hachurer le domaine D sur le graphique.
b. Calculer, en unité d’aire, l’aire du domaine D, puis en donner une valeur approchée à 10−2 près en cm2.
Aire du domaine D : A =H(1,5 p) - H(-0,5p) = -0,5 [ cos (1,5 p)+ sin (1,5 p)+2]e-(1,5 p)+0,5[ cos (-0,5 p)+ sin (-0,5 p)+2]e0,5 p.
A = -0,5(0-1+2)e-(1,5 p)+0,5(0-1+2)e0,5 p.
A = -0,5e-(1,5 p)+0,5e0,5 p ~ -0,0045 +2,41 ~2,40 unités d'aire soit 2,40 x4 =9,60 cm2.
Polynésie.
On considère la fonction f définie sur l’intervalle [0 ; +oo[ par f (x) = k e-kx où k est un nombre réel strictement positif.
On appelle Cf sa représentation graphique dans le repère orthonormé.
On considère le point A de la courbe Cf d’abscisse 0 et le point B de la courbe Cf d’abscisse 1.
Le point C a pour coordonnées (1 ; 0).
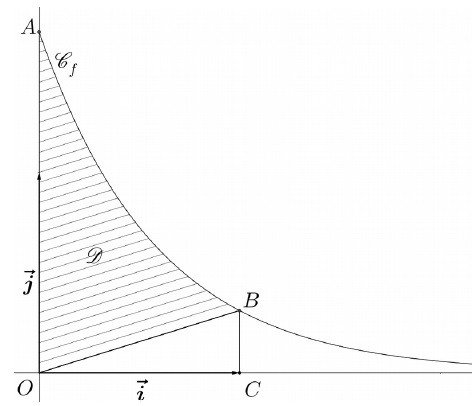
1. Déterminer une primitive de la fonction f sur l’intervalle [0 ; +oo[.
F(x) = - e-kx.
En effet : F '(x) = - (-k) e-kx = k e-kx = f(x).
2. Exprimer, en fonction de k, l’aire du triangle OCB et celle du domaine D délimité par l’axe des ordonnées, la courbe Cf et le segment [OB].
Ordonnée du point B : f(1)=k e-k.
Aire du triangle OCB = OC * BC / 2 =1 * ke-k / 2 = 0,5 ke-k.
Aire du domaine D = F(1)-F(0) - 0,5 ke-k.
F(1) = -e-k ; F(0)= -1 ;
Aire du domaine D = -e-k +1 - 0,5 ke-k= 1 -e-k (1+0,5 k).
3.
Montrer qu’il existe une unique valeur du réel k strictement positive
telle que l’aire du domaine D vaut le double de celle du triangle OCB.
1 -e-k (1+0,5 k) =2 *0,5 ke-k.
1 = ke-k +e-k (1+0,5 k) = e-k (1+ 1,5k).
1-e-k -1,5 k e-k=0.
On pose g(x) = 1-e-x -1,5 x e-x.
g'(x) = e-x-1,5(e-x-x e-x) = e-x(-0,5 +1,5x).
La fonction e-x est strictement positive, g'(x) est du signe de 1,5 x-0,5.
Sur [0 ; +oo [, g'(x) = 0 pour x = 1 / 3.
g'(x) >0 pour x >1 /3 et négative pour x < 1 / 3.
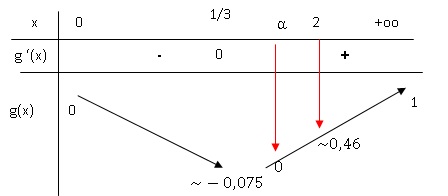
Sur [0 ; 1 / 3] la fonction g(x) est strictement décroissante et g(x) est négative.
L'équation 1-e-x -1,5 x e-x=0 n'a pas de solution sur cet intervalle.
Sur [ 2 ; +oo [ la fonction g(x) est strictement croissante et g(x) est positive.
L'équation 1-e-x -1,5 x e-x=0 n'a pas de solution sur cet intervalle.
La fonction g est continue et strictement croissante sur [1 / 3 ; 2 ].
La valeur zéro appartient à l'intervalle [( g(1/3) ; g(2)].
D'après le corollaire des valeurs intermédiaires, l'équation g(x) = 0 admmet une unique solution a sur [1 / 3 ; 2].
|
....
|
Nlle Calédonie.
Soient f et g les fonctions définies sur ]0 ; +∞[ par f (x) = e−x et g (x) =1 / x2 e-1/x.
On admet que f et g sont dérivables sur ]0 ; +∞[. On note f ′ et g ′ leurs fonctions dérivées respectives.
Les représentations graphiques de f et g dans un repère orthogonal, nommées respectivement Cf et Cg sont données ci-dessous
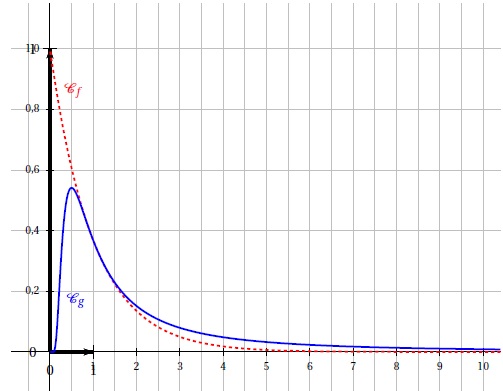
Partie A – Conjectures graphiques.
Dans chacune des questions de cette partie, aucune explication n’est demandée.
1. Conjecturer graphiquement une solution de l’équation f (x) = g (x) sur ]0 ; +∞[.
Abscisse de l'intersection des deux courbes : x = 1.
2. Conjecturer graphiquement une solution de l’équation g ′(x) = 0 sur ]0 ; +∞[.
Abscisse du maximum : x = 0,5.
Partie B – Étude de la fonction g.
1. Calculer la limite de g (x) quand x tend vers +∞.
1 / x tend vers zéro ; e-1/x tend vers e0 = 1 ; 1/x2 tend vers zéro ; produit des limites g(x) tend vers zéro.
2. On admet que la fonction g est strictement positive sur ]0 ; +∞[.
Soit h la fonction définie sur ]0 ; +∞[ par h(x) = ln(g (x)).
a. Démontrer que, pour tout nombre réel x strictement positif,
h(x) =(−1−2x ln(x) ) / x.
ln(1 / x2 e-1/x)=ln(1 / x2) +ln(e-1/x) = -ln(x2) -1 /x = -2ln(x) -1 / x = (-2x ln(x)-1) / x.
b. Calculer la limite de h(x) quand x tend vers 0.
x ln(x) tend vers zéro ;(-2x ln(x)-1) tend vers -1 ; -1 / x tend vers moins l'infini.
h(x) tend vers moins l'infini quand x tend vers zéro.
c. En déduire la limite de g (x) quand x tend vers 0.
g(x) = eh(x) ; eh(x) tend vers zéro quand x tend vers zéro.
3. Démontrer que, pour tout nombre réel x strictement positif,
g ′(x) =e− 1/x (1−2x) / x4 .
On pose u = 1 /x ; u' = -1 /x2.
g(x) = u2 e-u ; on pose v = u2 et w = e-u ;
v' = 2uu' = -2/ x3 ; w' = -e-u u'= e-1/x/x2.
v' w + w' v = -2e-1/x / x3 +e-1/x / x4 =e-1/x/ x4 (1-2x)
4. En déduire les variations de la fonction g sur ]0 ; +∞[.
e-1/x/ x4 est toujours positif.
Le signe de g'(x) est celui de (1-2x).
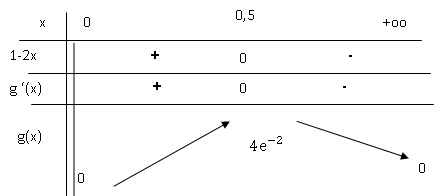
Partie C – Aire des deux domaines compris entre les courbes Cf et Cg.
1. Démontrer que la point A de coordonnées (1 ; e−1) est un point d’intersection de Cf et Cg .
On admet que ce point est l’unique point d’intersection de Cf et Cg , et que Cf est au dessus de Cg sur l’intervalle ]0 ; 1[ et en dessous sur l’intervalle ]1 ; +∞[.
e−x = 1 / x2 e-1/x ; e−x = 1 / (x2 e1/x ) ; x2 e-x e1/x = 1 ;
ln(x2) +ln(e-x) + ln(e1/x) = ln(1) = 0 ;
2ln(x) -x +1/x = 0 ; solution de cette équation x = 1 ; par suite f(1)=g(1) = e-1.
2. Soient a et b deux réels strictement positifs. Démontrer que
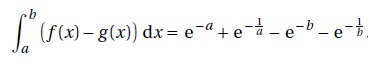
On pose u = 1 / x ; u' = -1/x2 : g(x) = -u' e-u ; primitive de g(x) :e-u =e-1/x ;
primitive de f(x) : -e-x.
Par suite : [-e-x -e-1/x]ba = -e-b -e-1/b +e-a +e-1/a.
3. Démontrer que 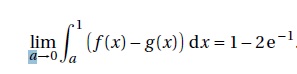
Quand a tend vers zéro : e-a tend vers 1 ; e-1/a tend vers zéro ;
Quand b est égal à 1 : -e-b = -e-1 et -e-1/b = -e-1 ;
par suite -e-b -e-1/b +e-a +e-1/a tend vers 1-2e-1.
4. On admet que
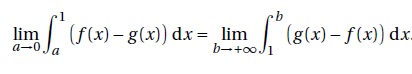
Interpréter graphiquement cette égalité.
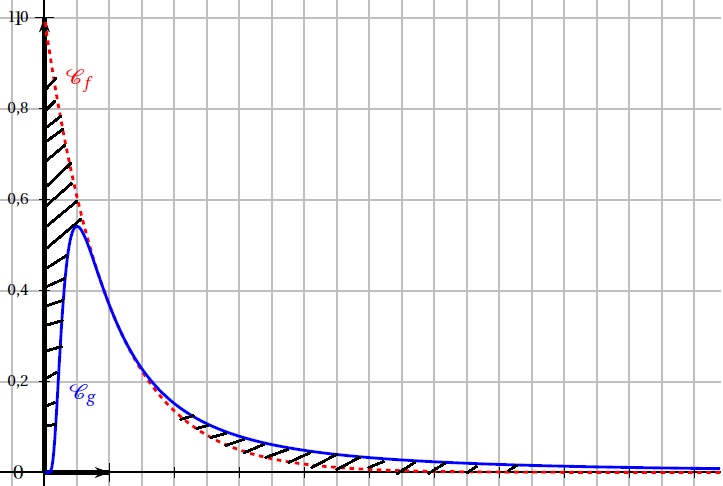
Les aires hachurées sont égales.
|
|