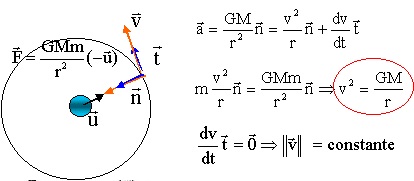Positionnement
par satellite, bac S Nlle Calédonie 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
| .
. |
......
.....
|
intensité de la pesanteur terresdtre g = 9,8 m s-2.
G = 6,67 10-11 N m2 kg-2.
Masse de la terre M = 5,97 1024 kg.
Rayon de la terre R = 6371 km.
1. Etude du mouvement du satellite dédié au repérage des balises ARGOS.
Le satellite de masse m se trouve sur une orbite polaire circulaire à
une altitude h = 850 km. Il peut recevoir les ondes émises par les
balises ARGOS flottant à la surface des océans.
L'étude est faite dans le référentiel géocentrique.
1.1. Exprimer la force exercée par la terre sur le satellite. On pose r = R +h.
1.2. On considère que le satellite est animé d'un mouvement circulaire uniforme. Montrer que la vitesse v du satellite est v2 = GM / (R+h).
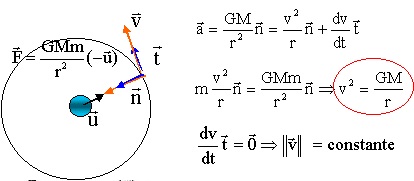
1.3. En déduire la valeur de cette vitesse en km /s.
v = [(6,67 10-11 x5,97 1024 /(6371 +850) 103)]½ =7,43 103 m /s = 7,43 km /s.
1.4. Calculer la valeur de la période de révolution T de ce satellite.
Le satellite décrit la circonférence 2 p(R+h) à la vitesse v en T seconde.
T = 2 p(R+h) / v = 2 x3,14 x(6371 +850) 103 / (7,43 103) ~6106 s ou 1 h 42 min.
2. Détermination de la position des balises au sol.
Les balises émettent une onde électromagnétique périodique de fréquence fL = 401,6500 MHz.
2.1. Déterminer le domaine du spectre électromagnétique auquel appartient cette onde.

Longueur d'onde l = c / f = 3,00 108 /(401,6500 106) ~0,75 m ou 7,5 108 nm. ( limite entre les micro-ondes et les ondes radio).
L'onde émise par la balise est reçue par le satellite et analysée pour en extraire la fréquence..
Le graphique ci-dessous reproduit les valeurs simulées de la fréquence
de l'onde reçue par la satellite au cours du temps. l'acquisition de
l'onde débute à t0 = 12 h 56 min 12 s.
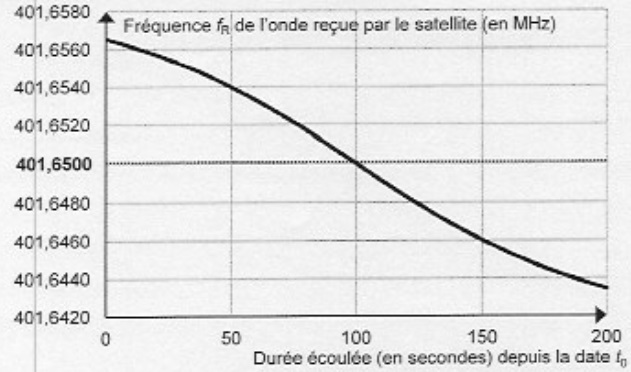
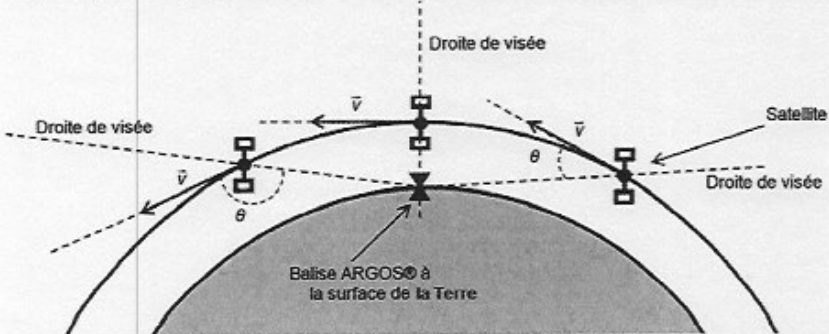
Cette variation de fréquence est imputable à l'effet Doppler. fR = fE( 1 +v cos q / c).
Au cours de son mouvement le satellite passe à la verticale de la
balise. On ne prend pas en compte le mouvement de la balise dans le
référentiel géocentrique.
2.2. Indiquer à t0 si le satellite s'approche ou s'éloigne de la balise. Justifier.
A partir de t0, la fréquence reçue fR est supérieure à fE. cos q est positif ; le satellite s'approche de la balise.
2.3. Déterminer l'heure à laquelle le satellite s'est approché au plus près de la balise. Justifier.
A la verticale de la balise q = 90 ° et fE = fR =401,6500 MHz.
t0 + 100 s =12 h 57 min 52 s.
2.4. Expliquer comment cette méthode permet de déterminer la position des balises à la surface du globe.
Lors de l'approche de la balise, fR est supérieure à fE.
Lors de l'éloignement de la balise, fR est inférieure à fE.
A la verticale de la balise fR = fE. Les positions de la balise et celle du satellite sont identiques.
|
|
.
|
....
|
3. Envoi du satellite dans l'espace.
L'étude est conduite durant la première seconde juste après le décollage dans le référentiel terrestre suppposé galiléen.
Les actions de l'air sont alors négligeables.
Masse totale au décollage : 228 103 kg.
Propulseur du premier étage : poussée durant la première seconde : F1 = 890 103 N.
Durée de la combustion : 265 s.
Masse de carburant consommé pendant cette durée : 100 103 kg.
Propulseurs d'appoint : 9.
Poussée durant la première seconde de chaque propulseur : Fp = 493 103 N.
Durée de la combustion : 64 s.
Masse de carburant consommée par chaque propulseur pendant cette durée : 11,7 103 kg.
D'après spaceflight101.net.
Durant la première minute du décollage, seul le premier étage et quelques uns des propulseurs d'appoint sont allumés.
Durant la première seconde juste après le décollage, la masse de la fusée est constante en négligeant la masse des gaz éjectés.
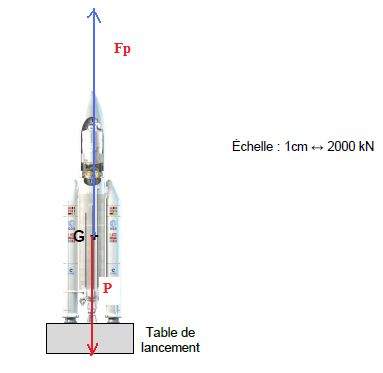
3.1. Dresser un
bilan qualitatif des forces qui s'exercent sur la fusée et les
propulseurs dans les premiers instants après le décollage. Les
représenter sur un schéma.
La fusée est soumise à son poids, verticale vers le bas, et à la poussée, verticale vers le haut, supérieure au poids.
3.2. Etude du décollage.
3.2.1. Montrer que la fusée ne peut pas décoller en utilisant uniquement le propulseur du premier étage.
Poids de la fusée : mg = 228 103 x9,8 =2,23 106 N, valeur supérieure à la poussée du premier étage 8,90 105 N.
3.2.2. Déterminer le nombre minimum de propulseurs d'appoint à utiliser.
La poussée totale doit être supérieure au poids.
8,90 105 + 4,93 105 x > 22,3 105 ;
8,9 +4,93 x > 22,3 ;
4,93 x > 13,4 ; x > 2,7 soit trois propulseurs d'appoint.
3.3. Pour le décollage le premier étage et six propulseurs d'appoint sont activés.
3.3.1 Déterminer la valeur de l'accélération et commenter.
valeur de l'accélération a = (poussée totale - poids) / masse.
a =(6 x4,93 105 +8,90 105) / (2,28 105) ~16,9 m s-2.
Soit environ le double de la valeur de l'accélération de la pesanteur 9,8 m s-2.
3.3.2. Estimer la masse de carburant consommé pendant la première seconde.
100 / 265 + 6x11,7 / 64 ~0,377 +1,096 ~1,5 tonnes.
3.3.3 L'hypothèse concernant la masse de la fusée est-elle valable. Justifier.
1,5 / 228 x100 ~0,6 % de la masse totale du lanceur.
L'hypothèse d'une masse constante est justifiée.
|
|