Le canon de Paris, bac S Am�rique du sud  2019. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . ...... ..... Souvent confondu � tort avec la grosse Bertha, le canon de Paris est � la fois le plus c�l�bre et le plus myst�rieux des canons de toute l'histoire de l'artillerie. Ce canon a bombard� Paris � la fin de la Premi�re Guerre mondiale. Le tube du canon mesure 36 m et p�se plus de 100 tonnes. La longueur et la masse exceptionnelles du canon ont oblig� les ing�nieurs de la soci�t� allemande Krupp � concevoir un syst�me de sout�nement in�dit en artillerie. Comme pour un pont suspendu, des haubans et un m�t central viennent rigidifier le long tube, l'emp�chant de se courber sous son propre poids. Mont�, le canon de Paris atteignait la masse de 750 tonnes. Mais le secret du canon de Paris r�side dans la trajectoire de l'obus. Avec une �l�vation �gale � 50 degr�s, le projectile est propuls� dans la haute atmosph�re o� l'air rar�fi� oppose moins de r�sistance � l'obus et accro�t ainsi sa port�e. Le 30 janvier 1918, lors des essais finaux au pas de tir de la marine � Altenwalde, le canon tira un obus de 105 kg avec une vitesse d’�jection de 1600 m.s-1. La dur�e de vol de l’obus a �t� de 176 s et il est tomb� � 126 km de distance avec une assez bonne pr�cision. Les obus ont atteint une altitude de 42 km � l'apog�e de leur trajectoire. C'�tait � l'�poque la plus haute altitude jamais atteinte par un projectile lanc� par l'homme. Le canon de Paris conserva ce record de 1918 � 1939. D’apr�s : http://html2.free.fr/canons/canparis.htm Le but de cet exercice est de v�rifier quelques donn�es de ce document sur le vol de l’obus. Intensit� de la pesanteur : g = 9,8 m.s-2. On se place dans le r�f�rentiel terrestre suppos� galil�en. On n�gligera les frottements et la pouss�e d’Archim�de. L’obus sera assimil� � un point mat�riel. 1. Expulsion de l’obus. On suppose que le syst�me {tube du canon + obus} est pseudo-isol� pendant cette phase d’expulsion, c'est-�-dire que l'ensemble des forces ext�rieures appliqu�es au syst�me se compensent. 1.1. Comment varie la quantit� de mouvement du syst�me pendant cette phase de tir ? Le syst�me �tant pseudo-isol�, la quantit� de mouvement du syst�me reste consatnte. 1.2. En d�duire la vitesse de recul du tube lors de l’expulsion de l’obus. Quantit� de mouvement initiale : z�ro. Quantit� de mouvement apr�s le tir : 100 x 103 Vrecul = 105 x1600 ;  Vrecul = 1,68 m /s. 1.3. Quelle serait cette vitesse si le tube �tait 10 fois plus l�ger (10 tonnes) ? Justifier la masse importante du tube du canon de Paris La vitesse de recul du tube serait 10 fois plus grande ( 16,8 m /s). Cela risquerait de d�teriorer le tube. 2. 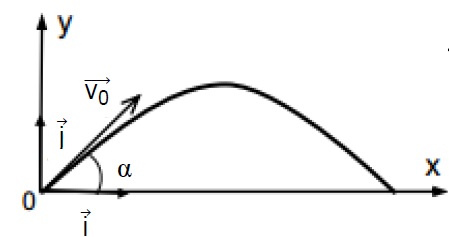Trajectoire de l’obus On �tudie le mouvement de l’obus dans le rep�re xOy donn� ci-dessous. Le point O est la gueule du canon (l’endroit o� l’obus sort du tube du canon). L’angle α entre le tube du canon et le sol correspond � l’�l�vation cit�e dans le document. v0 est le vecteur vitesse initiale de l’obus � la sortie du canon. 2.1. En utilisant une loi de Newton, d�terminer les coordonn�es du vecteur acc�l�ration de l’obus : ax(t) suivant l’axe x et ay(t) suivant l’axe y. L'obus n'est soumis qu'� son poids, la pouss�e d'Archim�de et les frottements �tant n�glig�s. ax(t)=0 et ay(t) = -g. 2.2. En d�duire les expressions des coordonn�es vx(t) et vy(t) du vecteur vitesse de l’obus et montrer que les �quations horaires du mouvement de l’obus s’�crivent : x(t)= v0 cos (α) t y(t)= -�gt2 +v0 sin a t. avec t en secondes, v0 en m�tres par seconde et x(t) et y(t) en m�tres. La vitesse est une primitive de l'acc�l�ration et les composantes de la vitesse initiale sont :v0 cos a  ; v0 sin a . . vx(t)  = v0 cos (α) et vy(t) =-g t + v0 sin (α) La position est une primitive de la vitesse et la position initiale est l'origine du rep�re. x(t)= v0 cos (α) t y(t)= -�gt2 +v0 sin a t. 2.3. En d�duire l’�quation de la trajectoire y = f(x). t = x(t) / ( v0 cos (α)) ; repport dans y(t) : y = -�gx2 / ( v0 cos (α))2 +x tan (α) . . .... 3. V�rification des donn�es du document 3.1. En utilisant la question 2.2, d�terminer la dur�e du vol et la port�e th�orique (distance entre le canon et l’endroit o� l’obus touche le sol). On n�gligera la hauteur du canon et on suppose que l'obus arrive � la m�me altitude que celle de son point de d�part. Au sol y(t) = 0 = -�gt2 +v0 sin a t. -�gt + v0 sin a  = 0 ; t =2 v0 sin a  / g = 2 x1600 x sin 50 / 9,8 ~ .2,5 102 s. Port�e th�orique: x = 1600 xcos 50 x 2,5 102 ~2,6 105 m ou 260 km. 3.2. D�terminer l’altitude th�orique maximale atteinte par l’obus connaissant l’expression de la composante verticale de la vitesse de l’obus : vy = - 9,8�t + 1226. A l'altitude maximale, la composante verticale de la vitesse est nulle. t = 1226 / 9,8 = 125 s. Altitude maximale atteinte : -0,5 x 9,8 x 1252 +1600 x sin 50 x 125 =7,7 104 m ou 77 km. 3.3. Expliquer l'�cart existant entre les r�sultats th�oriques obtenus dans les deux questions pr�c�dentes et les donn�es du document. En r�alit�, les frottements doivent �tre pris en compte.   .

menu