Physique,
concours Orthoptie Paris Descartes 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice I.
1. Si l'accélération d'un mobile est nulle :
A - Le mobile est nécessairement au repos. Faux.
B - La vitesse du mobile est constante. Vrai.
C - Le mobile peut avoir une trajectoire circulaire. Faux.
Le vecteur vitesse étant constant, le mouvement est rectiligne uniforme.
2. Si les forces agissant sur le mobile se compensent :
A - La trajectoire du mobile peut être rectiligne uniforme. Vrai.
B - La trajectoire du mobile peut être circulaire uniforme. Faux.
C - La trajectoire du mobile peut être rectiligne uniformément accélérée. Faux.
3. Lors d'une chute libre :
A - Le mobile n'est soumis qu'à la force de pesanteur. Vrai.
B - La trajectoire est rectiligne uniforme. Faux.
C - La trajectoire peut être parabolique. Vrai.
4. Dans le système solaire :
A - La période de révolution des planètes proches du soleil est plus grande que celle des planètes plus éloignées, Faux.
3ème loi de Kepler : T2 / r3 = constante. La période et le rayon de l'orbite varient dans le même sens.
B - L'accélération d'une planète, en ne tenant compte que du sytème planète- soleil, a une direction fixe. Faux.
L'accélération est centripète, dirigée vers le centre du soleil.
C -La trajectoire d'une planète est une ellipse autour du soleill. Vrai.
5. Le phénomène d'impesanteur.
A - correspond à un objet soumis à aucune force. Faux.
B - correspond à un objet immobile dans l'espace.
Faux.
C. Correspond à un objet en chute libre. Faux.
L'ensemble des forces gravitationnelles et inertielles possèdent une résultante et un moment résultant nuls.
6. Dans un système soumis à aucune force de frottement :
A. L'énergie potentielle est constante. Faux.
B.L'énergie mécanique est constante. Vrai.
C. Le mouvement est uniforme. Faux.
7. Dans un mouvement circulaire.
A. le vecteur vitesse est constant. Faux.
B. L'accélération est constante. Faux.
C. L'accélération est centripète. Faux.
|
|
|
Exercice II. Transmission de l'information.
1.1. Indiquer, à l’aide d’un tableau, les trois procédés de transmission de
l’information évoqués
ainsi que leurs avantages et inconvénients.
Procédé
|
Avantages
|
Inconvénients
|
Fibre
optique
|
Très
haut débit
Faibles pertes en puissance et compatibilité avec les amplificateurs
optiques
Insensible au champ magnétique
|
Coûteux et long à mettre en oeuvre si on doit relier toutes les habitations.
|
Réseau
cuivre
|
Rapide
à mettre en oeuvre et moins coûteux que la fibre optique.
|
Insuffisant
pour le très haut débit.
L'amortissement augmente avec la longueur.
Les champs magnétiques peuvent déformer les signaux.
|
Technologies
hertziennes
|
destinées
aux habitats très isolés.
|
|
1.2. Quels modes de
transmission correspondent à une propagation guidée ou libre ?
Justifier.
La transmission est
guidée dans les fibres optiques et les câbles en cuivre. La
transmission est libre ( dans toutes les directions ) dans le cas des
technologies hertziennes.
1.3. La communication optique pour la transmission d’information utilise un
faisceau laser. Rappeler les principales propriétés d’un faisceau laser.
Faisceau très directif,
quasiment monochromatique, grande puissance par unité de surface.
1.4. La fréquence des signaux transmis par satellite pour la communication
internet est de l’ordre de 20 GHz. Quelle est la longueur d’onde de ces signaux ?
l = c / f = 3,0 108
/ (20 109)=0,015 m = 1,5 cm.
Ces signaux sont-ils susceptibles d’être significativement diffractés
par des objets à la surface de la Terre tels que des immeubles ou des
collines ?
Non, la longueur d'onde
de ces signaux n'est pas du même ordre de grandeur que les dimensions
des immeubles ou des collines.
En déduire quelle doit être l’orientation des antennes des relais
terrestres par rapport aux satellites géostationnaires pour permettre la transmission internet.
Les satellites
géostationnaires sont dans le plan équatorial et paraissent fixes pour
un observateur terrestre. Les antennes terrestres doivent être dirigées
vers ce plan, c'est à dire vers le sud pour la France.
Transmission à longue distance.
2.1. Retrouver la valeur de la vitesse de propagation de la lumière dans une
fibre optique donnée dans l’article du magazine.
Célérité de la lumière
dans le vide divisée par l'indice de la fibre ~200 000 km/s.
2.2. Vérifier que l’atténuation linéique d’un signal transmis par
fibre optique est de 0,18 dB.km-1.
Atténuation A = 10 log (Pentrée /Psortie) ; Psortie = 0,96 Pentrée au bout d'un kilomètre de fibre.
A = 10 log (1/0,96) ~0,18
dB km-1.
Comparer cette valeur à celle d’un signal transmis par un câble
électrique qui est de 10 dB.km-1.
Conclure sur un des intérêts de la fibre optique.
10 / 0,18 ~56.
L'atténuation est environ
56 fois plus faible dans une fibre optique que dans un câble cuivre. Le
nombre d'amplificateurs sera bien moindre dans le cas d'une fibre
optique.
2.3. La longueur d’un système de communication par fibre optique qui relie
New-York à Brest est d’environ 7500 km. Quelle atténuation devrait-on constater sans
amplificateur optique sur un signal
transmis entre ces deux villes ? En déduire la perte en puissance
correspondant à cette
atténuation. Comparer cette valeur avec celle indiquée dans le document
sur la fibre optique.
A=7500
* 0,18 = 1350 dB.
Pentrée /Psortie = 10135 ; Psortie =10-135
Pentrée, valeur
correspondant à celle du texte.
Latence.
Les élèves d’un lycée newyorkais ont réalisé un blog hébergé sur un
serveur aux États-Unis. La taille moyenne d’une page du blog est de
1000 Ko.
3.1. À l’aide des notions de durée de propagation et de durée de
transmission, interpréter la phrase : « L’intérêt de la fibre optique
réside non pas dans sa « vitesse », mais dans la possibilité d’y
propager des données […] à un débit, c’est-à-dire un nombre de bits par
seconde, largement supérieur à celui accessible dans les autres
matériaux connus ».
La latence est le délai
minimum de transmission dans les communications informatiques. Ce délai
correspond à la durée de transmission ajoutée à la durée de propagation.
- La durée de
transmission Dt est le temps nécessaire pour transmettre
une quantité de données :
Dt = n / D avec D débit binaire en bit.s-1
et n taille du message en bit.
1000 Ko = 1000 *1024*8 =
8000 kbits ~ 8,2 106 bits.
Le très haut débit
correspond au moins à 30 Mbits /s soit 3,0 107
bits / s.
Dt =8,2 106 / (3,0 107) ~0,27 s.
-
La durée de propagation correspond à la durée nécessaire pour que les
données aillent de l’émetteur au récepteur.
7500 / 200 000 ~0,037 s.
La durée de propagation est inférieure à la durée de transmission. C'est la durée de transmission qui fait l'interêt d'une liaison.
3.2. Quelle est la durée de transmission d’une page du blog lorsque 15
élèves d’un établissement offrant un débit à 3 Mbits.s-1 se
connectent individuellement et simultanément à celle-ci ? Quel est
l’intérêt du Très Haut Débit pour les établissements scolaires ?
15 *8,2
106 = 1,23 108 bits ; 1,23 108 /(3 106)
~41 s.
Le très haut débit permet d'afficher rapidement ( en quelques seconde)
les pages du site.
3.3. Estimer la
durée de propagation qu’observerait un élève résidant en France pour
consulter la page du blog hébergé aux États-Unis.
7500 / 200 000 ~0,037 s.
3.4. Doubler le débit d’un
établissement français permettra-t-il de diviser par deux la latence
observée pour consulter une page du blog hébergé aux États-Unis ?
Vous justifierez votre réponse de manière quantitative en considérant
le chargement de la page du blog depuis un établissement ayant un débit
de 100 Mbit.s-1.
Non. En doublant le
débit, on divise par deux la durée de transmission ; par contre la
durée de propagation ne change pas.
Débit de 100 Mbit.s-1
: Dt = n / D = 8,2 106 / (1,0 108) ~0,082 s = 82 ms..
Durée de propagation : 0,037 s = 37 ms ; latence : 82+37 =119 ms.
Débit de 200 Mbit.s-1
: Dt = n / D = 8,2 106 / (2,0 108) ~0,041 s = 41 ms..
Durée de propagation : 0,037 s = 37 ms ; latence : 41+37 =78 ms.
|
|
|
|
Exercice III. Vol zéro G.
Au
printemps 2015, l’airbus A310 Zéro-G a réalisé ses premiers vols
scientifiques. Exploité par une filiale du Centre National d’Études
Spatiales (CNES), cet avion permet de simuler des conditions
d’apesanteur en décrivant des trajectoires paraboliques. Les
scientifiques peuvent ainsi mener des expériences sans avoir recours
aux missions spatiales.
Document 1 : Trajectoire parabolique de l’A310 Zéro-G
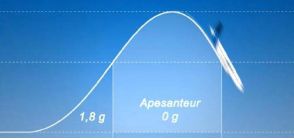
Pour que les passagers et le matériel embarqués dans l'Airbus A310
Zéro-G soient en apesanteur dans le référentiel de l'avion, et qu'ils
se mettent à y "flotter", il faut que l'avion soit en chute libre.
Dans le référentiel terrestre, un corps est en chute libre lorsque la
seule force qui s'exerce sur lui est le poids. Comment mettre l'avion
en condition de "chute libre", peut-on se demander. Rien de plus
"simple". Il suffit que le pilote de l'avion arrive à suivre la bonne
trajectoire parabolique.
Extrait d’un article de presse.
Document 2 : Caractéristiques du vol parabolique
Angle par rapport à l'horizontale au début de la parabole 47°
Altitude au départ et à la fin de la parabole 7 600 m
Vitesse au début de la parabole 527 km.h-1
Altitude au sommet de la parabole 8 200 m
Vitesse au sommet de la parabole 355 km.h-1
Durée d'apesanteur (0 g) 22 s.
Données :
- masse de l’airbus A310 Zéro-G et de son équipement : m = 1,5×105 kg ;
- constante de gravitation universelle : G = 6,67×10-11 m3.kg-1.s-2;
- intensité du champ de pesanteur à la surface de la Terre : g = 9,81 N.kg-1 ;
- masse de la Terre : M = 6,02×1024 kg ;
- rayon de la Terre : R = 6,38×106 m.
On se place dans le référentiel terrestre considéré comme galiléen sur la durée d’une parabole.
1. Étude du mouvement de chute libre.
On souhaite vérifier, par des considérations énergétiques, que la
trajectoire suivie par l’avion est modélisable par une chute libre.
1.1. Rappeler la condition que doit vérifier l’énergie mécanique d’un système lorsqu’il est en chute libre.
Un système en chute libre n'est soumis qu'à son poids ; le poids est
une force conservative. L'énergie mécanique d'un système en chute libre
est constante.
1.2. Les
caractéristiques de la trajectoire parabolique suivie par l’avion
sont-elles compatibles avec une chute libre de l’avion ? Argumenter
votre réponse avec un calcul d’énergie.
On prend l'altitude de départ et de fin de la parabole comme origine des altitudes, donc de l'énergie potentielle de pesanteur.
Energie mécanique au début de la parabole : ½mv2 avec v =527 / 3,6 =146,4 m /s.
Energie mécanique au sommet de la parabole :
½mvs2 +mgh avec vs = 355 / 3,6 = 98,6 m/s et h = 8200-7600 = 600 m.
Dans l'hypothèse d'une conservation de l'énergie mécanique : ( g étant supposé constant égal à 9,8 m/s2)
v2 = vs2 +2gh ; 146,42 = 98,62 + 2*9,8 *600 ;
2,14 104 = 2,14 104. L'hypothèse est validée.
2. Intensité du champ de pesanteur dans un vol Zéro-G.
2.1. En détaillant votre raisonnement, montrer que l’intensité de la pesanteur gh, en un point situé à l’altitude h au-dessus de la surface de la Terre, peut s’écrire :
gh =G M /(R+h)2.
Poids de l'avion : P = mgh ;
Force de gravitation exercée par la terre sur l'avion : F = GMm /(R+h)2.
P = F ; mgh = GMm /(R+h)2.
Simplifier par m : gh =G M /(R+h)2.
2.2.
Justifier, à partir du résultat précédent, qu’il est légitime de
considérer que l’intensité de la pesanteur est constante lors d’un vol
Zéro-G.
Au sol g0 = GM / R2 ; gh =g0[R /(R+h)]2 = g0[1 /(1+h / R)]2 ;
[1 /(1+h / R)]2 = 1 /(1 +8200 / (6,38 106)]2 =0,997.
gh =0,997g0. 3. Durée des phases d’apesanteur.
On étudie le mouvement dans le repère xOy donné ci-dessous, le point O
étant le début de la parabole. On considère que l’intensité de la
pesanteur terrestre est constante lors d’un vol Zéro-G et qu’elle est
égale à g = 9,8 N.kg-1.

3.1. Énoncer la deuxième loi de Newton.
Dans
un
référentiel galiléen, la somme vectorielle des forces extérieures
appliquées à un solide est égale à la dérivée par rapport au temps du
vecteur quantité de mouvement et si la masse est constante au produit
de la masse M du solide par
l'accélération de son centre d'inertie.
3.2. Montrer que les équations horaires x(t) et y(t) d’un système en chute libre ont pour expressions :
x(t) =v0 cos(a ) t ; y(t) =-½g t2 +v0 sin(a ) t.
ax = 0 ; ay = -g.
La vitesse est une primitive de l'accélération :
vx(t) = A ; vy(t) = -gt +B avec A et B des constantes déterminées par les conditions initiales.
vx(t) = v0 cos a ; vy(t) = -gt + v0 sin a .
La position est une primitive de la vitesse :
x(t) = v0 cos a t + C ; y(t)= -½gt2 + v0 sin a t +D, avec C et D des constantes déterminées par les conditions initiales x(t=0)=0 et y(t=0) = 0.
x(t) = v0 cos a t ; y(t)= -½gt2 + v0 sin a t .
|
|
3.3.
En exploitant les équations horaires, calculer la durée d’apesanteur.
Ce résultat est-il cohérent avec la donnée du document 2 ?
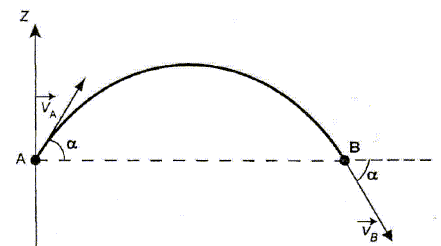
A la date tB, le système se trouve au
point B, de même altidude que le point A, avec une vitesse vB
= vA = 146 m/s.
vy A = -gtA + v0 sin a ; vy B = -gtB + v0 sin a ; vx A =vx B =v0 cos a ;
Par suite vy A = -vy B ; tB -tA = 2v0 sin a / g = 2*146 sin 47 / 9,8 ~22 s.
La valeur trouvée est cohérente avec le texte.
3.4. Quels paramètres faut-il modifier pour augmenter la durée d’apesanteur ?
tB -tA = 2v0 sin a / g
On peut augmenter la vitesse au début de la parabole ainsi que la valeur de l'angle a.
Cela est techniquement difficile à réaliser.
|
|