Physique,
concours orthoptie Nantes 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
I Comment déterminer le relief du fond marin avec un sondeur ? ( 8,5 points).
1. Etude de l'onde ultrasonore dans l'eau de mer..
1.1. Définir une onde mécanique progressive.
Propagation d'une perturbation ( modification d'une
propriété du milieu) dans un milieu
matériel, sans transport de matière, mais avec
transport d'énergie.
1.2 L'onde ultrasonore est-elle une onde longitudinale ou
transversale ? Justifier la réponse.
L'onde ultrasonore est onde longitudinale :
Propagation d'une variation de pression ayant la
même direction que la direction de propagation de
l'onde.
1.3 La lumière est une onde progressive
périodique mais elle n'est pas
mécanique.
- Citer un fait expérimental qui permet de
décrire la lumière comme une onde.
- Quelle observation permet de montrer que la
lumière n'est pas une onde mécanique ?
La diffraction de la lumière par une fente
dont les dimensions sont du même ordre de grandeur que
la longueur d'onde, est un fait expérimental qui
permet de décrire la lumière comme une
onde. Unee onde mécanique ne se propage pas dans le vide
; la lumière peut se propager dans le vide : la
lumière n'est donc pas une onde mécanique.
2. Détermination de la
célérité des ondes ultrasonores dans
l'eau :
La célérité
des ultrasons dans l'air vair = 340 m/s est plus
faible que la célérité des ultrasons
dans l'eau de mer veau.
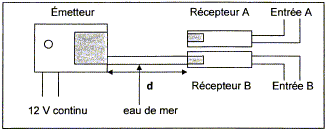
Un émetteur produit
simultanément des salves d'ondes ultrasonores dans un
tube rempli d'eau de mer et dans l'air (voir figure 1). A
une distance d de l'émetteur d'ondes ultrasonores,
sont placés deux récepteurs, l'un dans l'air
et l'autre dans l'eau de mer. Le récepteur A est
relié à l'entrée A du système
d'acquisition d'un ordinateur et le récepteur B
à l'entrée B. L'acquisition commence lorsqu'un
signal est reçu sur l'entrée B du
système.
2.1. Pourquoi est-il nécessaire de
déclencher l'acquisition lorsqu'un signal est
reçu sur l'entrée B ?
Les ondes ultrasonores se propagent plus vite dans l'eau
de mer que dans l'air : l'entrée B reçoit en
premier un signal, puis ensuite l'entrée A.
2.2. Donner l'expression du retard Dt
entre la réception des ultrasons par les deux
récepteurs en fonction de tA et
tB, durées que mettent les ultrasons
pour parcourir respectivement la distance d dans l'air et
dans l'eau de mer.
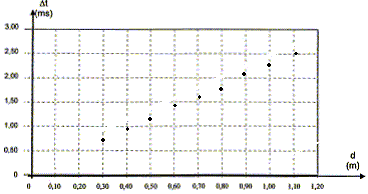
On détermine Dt
pour différentes distances d entre
l'émetteur et les récepteurs. On obtient le
graphe D t = f(d) ci-dessous :
- Donner l'expression de Dt
en fonction de d, vair, veau.
- Justifier l'allure de la courbe obtenue.
- Déterminer graphiquement le coefficient
directeur de la droite D t =
f(d). En déduire la valeur de la
célérité veau des
ultrasons dans l'eau de mer.
Dans l'air : d = vair tA.
(1)
dans l'eau : d = veau tB.
(2)
(1) -
(2) donne :
tA-tB = Dt
= d ( 1/vair - 1/veau).
vairet veau étant
constantes, Dt
et d sont proportionnelles : Dt
= a d avec "a " une constante égale à : a
=
( 1/vair -
1/veau).
Le graphe correspondant Dt =
f(d) est une droite passant par l'origine.
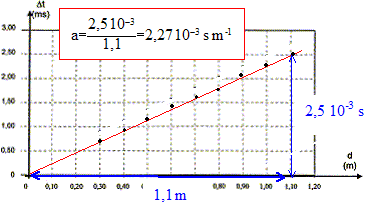
2,27 10-3 =
1/vair - 1/veau.
1/veau =
1/vair -2,27
10-3 = 1/340 -2,27
10-3 =6,71 10-4.
veau =1 /6,71
10-4
=1,5 103
m/s.
3. Détermination du
relief des fonds marins
Dans cette partie on prendra veau =
1,50103 m/s.
Un sondeur acoustique classique est composé d'une
sonde comportant un émetteur et un récepteur
d'onde ultrasonore de fréquence f = 200 kHz et d'un
boîtier de contrôle ayant un écran qui
visualise le relief des fonds sous-marins. La sonde envoie
des salves d'ultrasons verticalement en direction du fond
à des intervalles de temps réguliers ; cette onde
ultrasonore se déplace dans l'eau à une
vitesse constante veau. Quand elle rencontre un obstacle,
une partie de l'onde est réfléchie et
renvoyée vers la source. La détermination du
retard entre l'émission et la réception du
signal permet de calculer la profondeur p.
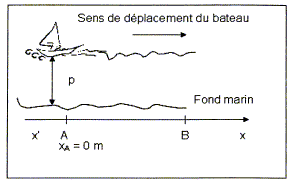
Un bateau se déplace en ligne droite suivant un
axe x'x en explorant le fond depuis le point A xA
= 0 m jusqu'au point B xB = 50 m.
Le sondeur émet des salves d'ultrasons à
intervalles de temps égaux, on mesure à l'aide
d'un oscilloscope la durée Dt
séparant l'émission de la salve de la
réception de son écho. L'oscillogramme ci-dessous montre l'écran d'un
oscilloscope lorsque le bateau se trouve en A (xA
= 0 m). L'une des voies représente le signal
émis, l'autre le signal reçu par le
récepteur. Sur l'oscillogramme, on a
décalé la voie 2 vers le bas pour istinguer
nettement les deux signaux.
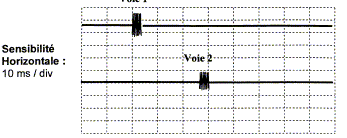
La figure 3 ci-dessous représente Dt
= f(x) lorsque le bateau se déplace de A vers B.
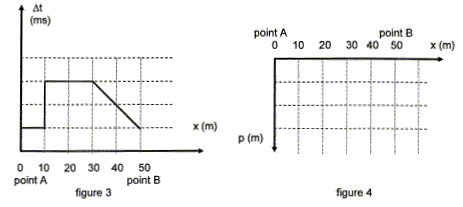
3.1 Identifier les signaux observés sur
chaque voie, en justifiant. A partir de l'oscillogramme,
déterminer la durée Dt
entre l'émission de la salve et la
réception de son écho. En déduire la
graduation de l'axe des ordonnées de la figure
3.
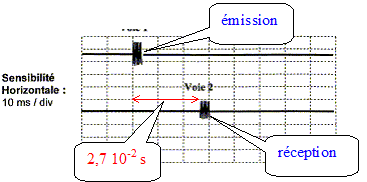
L'émission a lieu avant la réception de
l'écho.
Durée Dt
entre l'émission de la salve et la réception
de son écho : 2,7 10-2 s.
Graduation de l'axe des ordonnées de la figure
3 : une division correspond à
2,7 10-2
s.
3.2. Déterminer la relation permettant de calculer
la profondeur p en fonction de Dt
et veau.
aller + retour = 2 p = veau Dt
p = ½ veau
Dt
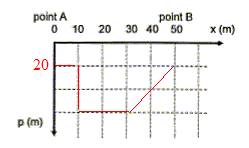
= 0,5*1500 * 2,7 10-2 = 20 m.3.3 Tracer sur la figure 4, l'allure du fond marin
exploré en précisant la profondeur p en
mètres en fonction de la position x du
bateau.
3.4. Le sondeur envoie des salves d'ultrasons à
intervalles de temps réguliers T. Pour une bonne
réception, le signal émis et son
écho ne doivent pas se chevaucher. Le sondeur est
utilisable jusqu'à une profondeur de 360 m.
Déterminer la période minimale
Tm des salves d'ultrasons permettant ce
fonctionnement.
2p = 2*360 = 720 m ; veau = 1500 m/s ;
Dt = 2p/veau
=720/1500 = 0,48 s.
Tm est
supérieure à 0,48 s.
|
|
|
II. Principe de la lecture d'un disque optique. 4 points.
Le
CD est en polycarbonate ( matière plastique transparente ) recouvert
d'une couche métallique réfléchissante ( aluminium en général ) elle
même protégée par un vernis. La face supérieure peut être imprimée ou
recouverte d'une étiquette.
Les informations sont stockées sous forme de plats ou de cuvettes sur
une spirale qui commence sur le bord intérieur d'un CD et finit sur le
bord extérieur. Les creux ( en anglais pit ) ont une profondeur de 0,12 µm et une largeur
de 0,67 µm.
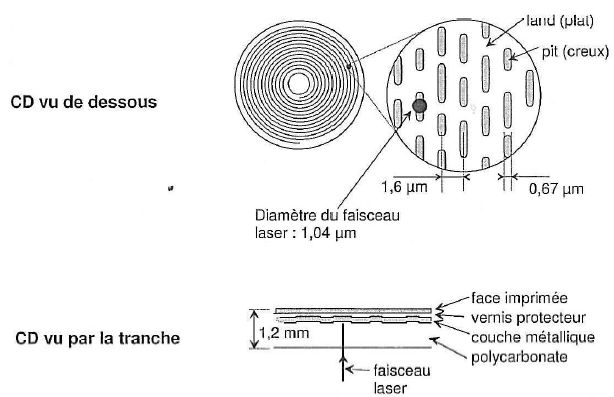
La tête de lecture est constituée d'une diode laser émettant une radiation de longueur d'onde dans le vide l0 = 780 nm et d'une photodiode détectant la lumière réfléchie par la surface métallisée du CD.
La
lumière émise par la diode traverse une lame semi-réfléchissante avant
de se réfléchir sur un miroir. La lentille assure la mise au point du
faisceau sur le disque. L'ensemble miroir lentille est monté sur un
chariot mobile qui permet au faisceau laser de balayer un rayon du
disque. La surface du disque défile devant le faisceau laser à une
vitesse de 1,2 m/s quelle que soit la position du faisceau.
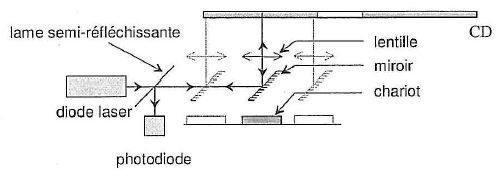
L'indice du polycarbonate est n = 1,55.
1.1. Calculer la célérité de l'onde lumineuse dans le CD.
v = c / n = 3,00 108 /1,55 =1,94 108 m/s.
1.2. En déduire la longueur d'onde l de la lumière dans le polycarbonate sachant que la fréquence ne dépend pas du milieu traversé.
l = v / f = l0 / n = 780/1,55 = 503 nm.
1.3. Vérifier que la profondeur d'un "pit" est de l'ordre de l / 4.
503 /4~ 126 nm = 0,126 µm.
1.4.
Déterminer, en justifiant, la différence de marche entre les rayons du
faisceau laser lors de la réflexion au passage plat / creux.
La différence de marche entre les ondes réfléchies par le fond de la cuvette et par le bord est égale à 2 h soit 0,5 l.
1.5. Expliquer pourquoi les interférences sont destructives au niveau du passage plat / creux.
Les interférences sont destructives car la différence de marche est un
multiple impair de la demi-longueur d'onde.
1.6. Que se passe t-il au niveau d'un creux ?
Lors de la détection d'un zéro, le faisceau est entièrement réfléchi par un plat
ou par un creux. Tous les rayons composant le faisceau ont donc parcouru le
même trajet. Les interférences sont constructives et l'éclairement de la photodiode est maximal.
Le problème de la diffraction.
Le bloc optique est constitué d'une diode laser suivi d'une lentille
convergente. Les diamètres de la diode et de la lentille sont très
faibles. Le faisceau subit donc une diffraction et l'image donnée par
la lentille n'est pas un point mais une petite tache ( appelée tache
d'Airy ). Le diamètre de la tache est d = 1,22 l / NA, avec NA, l'ouverture numérique.
La taille de cette tache limite le nombre d'informations que peut
stocker le CD car il faut que la tache du laser ne lise qu'une piste à
la fois. Pour augmenter la capacité de stockage, il faut modifier la
longueur d'onde du laser et l'ouverture numérique.
Type de support
|
CD
|
DVD
|
HD-DVD
|
Blu-ray
|
Longueur d'onde dans le vide
|
780 nmn
|
658 nm
|
405 nm
|
405 nm
|
NA
|
0,45
|
0,65
|
0,65
|
0,85
|
Capacité
|
700 Mbits
|
4,7 Gbits
|
15 Gbits
|
23 Gbits
|
Distance entre pistes
|
1,6 µm
|
0,74 µm
|
0,32 µm
|
0,4 µm
|
2.1. Calculer le diamètre de la tâche due à la diffraction pour un CD.
d = 1,22 x503 / 0,45 ~1363 nm ~ 1,4 µm.
2.2. Montrer que ce diamètre permet une lecture correcte des pistes.
d est inférieure à la distance entre les pistes.
2.3. Justifier que la distance entre les pistes sur un DVD peut être égale à 0,74 µm sachant que la largeur d'un pit vaut 0,32 µm.
2.4. Pour un DVD quelle doit être la profondeur d'un creux ?
Longueur d'onde dans le polycarbonate : 658 / 1,55 = 424,5 nm
424,5 / 4 ~106 nm ~0,106 µm.
2.5
Expliquer les choix techniques ( longueur d'onde et NA) faits pour un
DVD afin d'augmenter la capacité de stockage d'informations.
En augmenatant NA et en diminuant la longueur d'onde, on fait diminuer
le diamètre de la tache de diffraction. En conséquence les pistes
seront plus proches et la capacité de stockage sera augmentée.
|
|
|
|
III Les prouesses du poisson archer.
Etude
de texte.
«
La particularité du poisson archer est qu’il ne se contente pas
d’attendre le hasard d’une chute ou qu’un coup de vent providentiel
amène à lui cette manne céleste [les proies aériennes]. Il peut, en
projetant un puissant jet d’eau avec sa bouche, faire tomber des proies
en surface avant de les attraper […].
Après avoir repéré sa future
proie, le poisson s’oriente, se rapproche et se positionne. Le museau
affleure à la surface de l’eau mais les deux gros yeux situés près de
la bouche […] restent sous la surface […].
Précis, le tir du Toxotes
[poisson archer] est pourtant confronté à une difficulté balistique
majeure : pour viser, il lui faut tenir compte de la différence
d’indice de réfraction entre l’eau et l’air […].
Deux hypothèses ont
été proposées pour expliquer la précision du poisson archer. La
première est qu’il se positionne à la verticale de sa proie […]. Il
voit donc théoriquement l’insecte où il est vraiment. Cependant
l’observation montre que la majorité des tirs a lieu selon des angles
variant de 70° à 80°, aussi pense-t-on que plus probablement son
habileté résulte d’un apprentissage : c’est à force de rater sa cible
que le poisson corrigerait de lui-même la réfraction. On a en effet
déterminé expérimentalement qu’il est capable de tirer avec précision
environ 8 fois par minute sur une période de 10 minutes, ce qui lui
permet d’ajuster son tir si nécessaire. […]. »
Bruno Didier, Le poisson archer, Revue Insectes n°130, 2003,
Septembre, p23.
Indices de réfraction de l’air et de l’eau : nair
= 1,0 et neau = 1,33
Loi de Descartes : n1.sin i1
= n2.sin i2 avec i1
: angle d’incidence et i2 : angle de réfraction.
1. En prenant
appui sur le texte, nommer le phénomène physique mis en jeu lors de la
visée de l’insecte par le poisson. Dans
quelles conditions observe-t-on ce phénomène ?
La
réfraction d'un faisceau lumineux à la traversée de la surface séparant
deux milieux transparents d'indice de réfraction différents ( dioptre
eau-air dans ce cas ). Si le second milieu est moins réfringent que le
premier, le rayon réfracté peut ne pas exister.
2. Justifier
la phrase du texte : « Il voit donc théoriquement
l’insecte où il est vraiment ».
Le jet étant perpendiculaire à la surface de l'eau ( poisson à la
verticale sous l'insecte ), l'angle d'incidence i1
est nul. La formule de Descartes conduit à i2
=0. Un rayon lumineux perpendiculaire à la surface séparant l'eau de
l'air, n'est pas dévié.
3. Calculer
la fréquence f d’émission des jets d’eau.
" 8 fois par minute" : 8 / 60 = 0,13 ~1 10-1
Hz.
Modélisation du mouvement du jet d'eau.
Dans la suite de l’exercice, le comportement du jet d’eau sera assimilé à celui d’une goutte d’eau de masse m.
On note v0
le vecteur vitesse initiale du centre d’inertie de la goutte. Une
mouche posée sur une feuille située à une hauteur H = 75 cm au-dessus
de la surface de l’eau est convoitée par un poisson archer situé non
loin de là. Le poisson projette vers l’insecte un jet d’eau avec un
vecteur vitesse initiale v0 incliné d’un angle α par rapport
à l’horizontale. Le jet percute l’insecte au moment où l’eau atteint le
sommet de sa trajectoire.
Soit G le centre d’inertie de la goutte
d’eau et I le centre d’inertie de la mouche. Dans toute l’étude on
supposera que l’action de l’air est négligeable.
Le mouvement de G est étudié dans le référentiel terrestre supposé galiléen.
On
prend comme origine des dates, l’instant où le poisson archer projette
l’eau ; le point G se trouve alors au point O pris comme origine du
repère.
Données : Intensité du champ de pesanteur terrestre : g = 9,81 m.s-2 ; v0 = 4,0 m.s-1.
Vecteur vitesse.
Les coordonnées du vecteur vitesse sont : vx = v0 cos a ; vy =- gt +v0 sin a.
a. Exprimer les coordonnées du vecteur vitesse initiale v0 dans le repère.
v0 x = v0 cos a ; v0 y =v0 sin a.
b. Soit vx la coordonnée horizontale du vecteur vitesse. Expliquer qualitativement pourquoi on peut affirmer que vx garde une valeur constante au cours du mouvement.
La
seule force agissant sur la goutte est verticale. Cette force
n'effectue aucun travail lors d'un trajet horizontal. Le théorème de
l'énergie cinétique indique que la composante horizontale de la vitesse
reste constante.
Ou bien, la vitesse est une primitive de l'accélération et la composante horizontale de l'accélération est nulle.
c. Dessiner, sans souci d’échelle, le vecteur vitesse (noté vS ) du centre d’inertie G de la goutte, au moment de l’impact avec l’insecte, resté immobile au point représenté sur la figure.
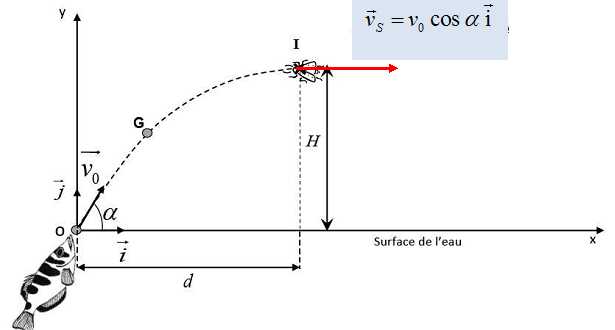
d. Exprimer les coordonnées de vS en fonction de v0 et α.
vS x = v0 cos a ; vS y =0.
2.2. Qu'implique la phrase " l'action de l'air est négligeable" ?
La goutte d'eau n'est soumise qu'à son poids ; la chute de cette goutte est libre. Son énergie mécanique reste constante.
2.3. Exprimer l’énergie mécanique du jet d’eau en fonction de m, v0, α, g et H.
Au point O, l'énergie mécanique est sous forme cinétique ( l'origine des altitudes étant prise en O).
E = ½mv02.
Au moment de l’impact avec la mouche, l'énergie mécanique est la somme de l'énergie cinétique et potentielle de pesanteur.
E = ½mv02cos2 a + mgH.
2.4. En déduire que la valeur de l’angle α permettant au jet d’eau d’atteindre la mouche vérifie l’équation : sin a = (2gH)½/v0.
La conservation de l'énergie mécanique s'écrit : ½mv02cos2 a + mgH = ½mv02.
v02(1-cos2 a ) = 2gH ; or sin2a = 1-cos2 a d'où : v02 sin2a =2gH ; sin a = (2gH)½/v0.
2.5. Vérifier que la valeur de l’angle α vaut 74°.
sin a = (2*9,81*0,75)½/4,0 =0,959 ; a = 73,53 ~74°. |
|
|
|
Eclairage d'un aquarium.
En
aquariophilie, on utilise comme éclairage des tubes fluorescents. Ce
type de tube contient de la vapeur de mercure à basse pression dans
laquelle on déclenche une décharge électrique. Le rayonnement
ultraviolet émis par le mercure est transformé en lumière visible par
une poudre fluorescente qui tapisse la paroi intérieure du tube. Le
spectre d’émission du tube dépend de la nature de la poudre
fluorescente utilisée.
Il existe une grande variété de tubes
fluorescents parmi lesquels on trouve des tubes avec la mention « plein
spectre » (lumière du jour). La figure suivante présente le spectre d’émission
d’un de ces tubes.
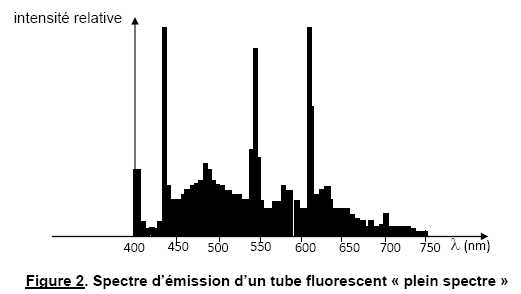
Données :
Longueurs
d’onde des principales raies d’émission du mercure dans le visible :
405 nm, 436 nm, 546 nm, 577 nm, 579 nm, 615 nm.
Constante de Planck : h = 6,63.10–34 J.s. Célérité de la lumière dans le vide : c = 3,00. 108 m.s–1.
1 eV = 1,60 10 –19 J.| couleurs | violet | bleu | vert | jaune | orange | rouge | | l (nm) | 400 - 424 | 424 - 491 | 491 - 575 | 575 - 585 | 585 - 610 | 610 - 750 |
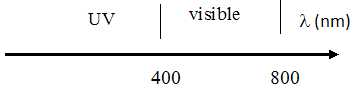
3.1. Situer le domaine des longueurs d’onde des ultra-violets par rapport au domaine des longueurs d’onde des radiations visibles.
À propos du spectre du tube fluorescent.
3.2a. Justifier l’appellation « plein spectre » de ce type de tube.
Sur la figure 2, toutes les couleurs de l'arc en ciel sont présentes avec une intensité relative non nulle.
3.2.b À partir du texte, indiquer le rôle du mercure dans le tube fluorescent.
La
lumière UV du mercure excite les atomes de la poudre qui tapisse la
paroi interne du tube. Cette poudre émet alors une lumière blanche.
À propos du mercure utilisé dans le tube fluorescent.
La figure 3 ci-dessous représente le diagramme simplifié des niveaux d’énergie de l’atome de mercure.

3.3a Quel nom donne-t-on au niveau d’énergie E0 ? Comment appelle-t-on les niveaux d’énergie E1 à E4 ?
E0 : niveau fondamental, de moindre énergie ; E1 à E4 : états excités.
L’une des radiations visibles émises par la vapeur de mercure
correspond à une transition faisant intervenir les niveaux d’énergie E1
et E3 du diagramme représenté.
3.3b Préciser le
sens de cette transition.
L'atome cède de l'énergie au milieu extérieur en émettant un photon.
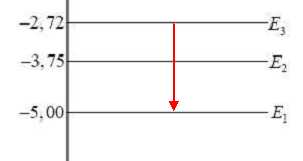
3.3c Calculer la valeur de la longueur
d’onde du photon émis lors de la transition. La valeur trouvée est-elle
cohérente avec les données de l’énoncé ?
DE = hc / l ; l = hc / DE avec DE =(5,00-2,72) *1,60 10-19 = 3,648 10-19 J.
l = 6,63 10-34 *3,00 108 / 3,648 10-19 = 5,45 10-7 m = 545 nm.
Cette valeur est cohérente avec la valeur 546 nm de l'énoncé.
|
|