QCM
mathématiques, concours Audioprothésiste Bordeaux 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 7.
Soit le nombre complexe z = 5 (cos q + i sin q).
Question 21
Le nombre complexe conjugué de z a pour argument à 2 p près.
A. q. Faux.
5 (cos q - i sin q)= 5( cos (-q) +i sin (-q)
B. -q. Vrai.
C. q + p. Faux.
D. q + p / 2. Faux
E. p/2-q. Faux.
Question 22
Le conjugué de z multiplié par i a pour argument à 2 p près :
A. q. Faux.
i cos q -i2 sin q = sin q + i cos q = cos ( p/2-q) +i sin( p/2-q).
B. -q. Faux.
C. q+p. Faux
D. q+p / 2.. Faux.
E.p / 2 -q. Vrai.
Exercice 8.
Soit le nombre complexe z = -3i exp(i 2p/3).
Question 23.
A 2 p près l'argument de z est :
A. 11 p /6. Faux .
z = 3 exp (-ip/2) exp(i 2p/3) = 3 exp(i( 2p / 3 - p / 2) = 3 exp(i p/6).
B. p /6. Vrai.
C. 5p /6.. Faux.
D. -p /6.. Faux.
E. p /2. Faux.
Question 24
A 2 p près l'argument de z3 est :
A. 11 p /6. Faux .
z = 3 exp (-ip/2) exp(i 2p/3) = 3 exp(i( 2p / 3 - p / 2) = 3 exp(i p/6).
z3 = 27exp(i 3p/6)=27 exp(i p/2).
B. p /6. Faux.
C. 5p /6.. Faux.
D. -p /6.. Faux.
E. p /2. Vrai.
Question 25
Le module de z3 est :
A. 9. Faux.
B. 3. Faux.
C. -9. Faux.
D. -3. Faux.
E. Aucune des solutions proposées ci-dessus n'est correcte. Vrai.
|
|
|
Exercice 9.
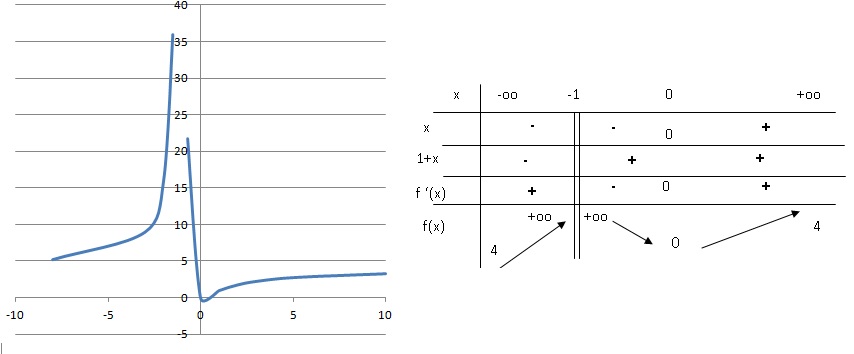
Soit la fonction définie par f(x) =4 x2 / (x+1)2.
Question 26. La limite en moins l'infini de f(x) est égale à :
A. plus l'infini. Faux.
B. moins l'infini. Faux.
C. zéro. Faux ( f(x) = 4 /(1+1 /x)2 et 1 / x tend vers zéro
D. 4. Vrai.
E.1. Faux.
Question 27
La limite en 0 de f(x) est égale à :
A. plus l'infini. Faux.
B. moins l'infini. Faux.
C. zéro. Vrai.
D. 4. Faux.
E. 1. Faux.
Question 28
La limite en 1 de f(x) est égale à :
A. plus l'infini. Faux.
B. moins l'infini. Faux.
C. zéro. Faux.
D. 4. Faux.
E. 1. Vrai.
Question 29.
La limite en -1 de f(x) est égale à :
A. plus l'infini. Vrai.
B. moins l'infini. Faux.
C. zéro. Faux.
D. 4. Faux.
E. 1. Faux.
Question 30.
Sur son ensemble de définition f est
A.strictement croissante. Faux.
B. strictement décroissante. Faux.
c. constante. Faux.
D. monotone. Faux
E. aucune des solutions proposées n'est correcte. Vrai.
On pose X = 2x /(1+x) et u = 2x et v = 1+x ; u' = 2 ; v' = 1.
(u'v-v'u) / v2 = (2(1+x)-2x) / (1+x)2 = 2 / (1+x)2.
f '(x) = 2 XX' = 4x / (1+x)3.
f '(x) est du signe de x / (1+x).
|
|
|
|
Question 31
Sur [0 ; +oo[ la fonction est :
A. strictement croissante . Vrai.
B. strictement décroissante . Faux..
C. constante . Faux.
D. non monotone. Faux.
E. Aucune des propositions proposées ci-dessus n'est vraie. Faux.
Question 32
Sur ]-1 ; 0] la fonction est :
A.strictement croissante. Faux.
B.strictement décroissante. Vrai.
C. constante.
Faux.
D. non monotone.
Faux..
E. Aucune des propositions proposées ci-dessus n'est vraie. Faux.
Exercice 10. Question 33
La valeur de l'intégrale suivante est :
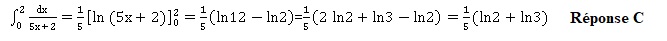
Question 34
La valeur de l'intégrale suivante est :
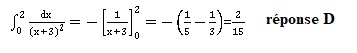
Question 35.
La valeur de l'intégrale suivante est :
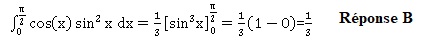
Question 36
La valeur de l'intégrale suivante est :
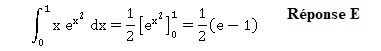
|
|
Question 37
Une primitive de la fonction cos(2x+3) sin(2x+3) est :
On pose u = sin (2x+3) ; u' = 2 cos (2x+3) ;
cos(2x+3) sin(2x+3) = ½uu'.
Une primitive de ½uu'.est u2 / 4 = 1/4 sin2(2x+3). Réponse C.
Question 38
Une primitive de la fonction 1 / x2 exp(1 / x) est :
On pose u = 1 / x ; u' = -1 / x2 ;
1 / x2 exp(1 / x) = -u' eu ; une primitive de -u' eu est -eu = - exp(1/x). Réponse A.
Exercice 12.
Soit X une variable aléatoire suivant une loi normale centrée réduite N(0 ; 1). Soit un nombre réel a :
Question 39
Alors la probabilité P(X< -2) :
A. est égale à 0,5. Faux.
B. est strictement inférieure à 0,5. Vrai.
C. est strictement supérieure à 0,5. Faux.
D. est négative. Faux.
E. aucune des propositions ci-dessus n'est correcte. Faux.
Question 40
La probabilité P(X < a) est :
A. est égale à 0,5. Faux, ( vrai si a = 0).
B. est strictement inférieure à 0,5. Faux, ( vrai si a est négatif)
C. est strictement supérieure à 0,5. Faux ( vrai si a est positif)
D. est négative. Faux.
E. aucune des propositions ci-dessus n'est correcte. Faux.
|
|