Mathématiques,
concours audioprothésiste Nancy 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
I. 6 points.
Pour tout nombre complexe z, de forme algébrique z = x + i y, on définit le nombre complexe z' suivant.
1. Déterminer les parties réelles et imaginaires de z' en fonction de x et y.
II. 5 points.
Pour tout nombre complexe z on pose : P(z) = z4 +2z3
+11z2 +2z+10.
1. Déterminer deux
racines imaginaires pures de l'équation P(z) = 0.
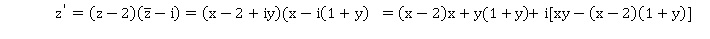2. Déterminer l'ensemble E des points M d'affixe z pour lesquels z' est réel.
xy -(x-2)(1+y)=0
xy-(x-2+xy-2y)=0
-x+2+2y=0 ; y = 0,5x -1.
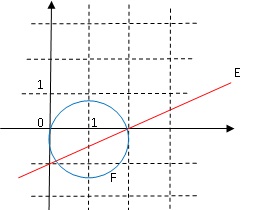
L'ensemble cherché est la droite d'équation y = 0,5 x-1.
3. Déterminer l'ensemble F des points M d'affixe z pour lesquels z' est imaginaire pur.
Démontrer que le point A d'affixe 2 appartient à F.
(x-2)x +y(1+y) = 0.
x2-2x+y2+y=0.
x2-2x+1+y2+y+0,25-1-0,25 =0.
(x-1)2 +(y+0,5)2 = 1,25.
L'ensemble F est un cercle centré au point de coordonnées ( 1 ; -0,5) et de rayon 1,25½.
A(2 ; 0) : (2-1)2 +(0+0,5)2 =1+0,25 = 1,25.
4. Représenter les ensembles E et F.
II. 3 points.
Déterminer :
1.a. Une primitive sur R des fonctions suivantes :
f1(x) = x3+1 ; F1(x) = x4 / 4 +x.
f2(x) =cos(3x) ; F2(x) =sin(3x) / 3.
f3(x) = e-3x ; F3(x) = e-3x / (-3).
1.b. Une primitive sur ]0 ; +oo[ des fonctions suivantes :
f4(x) =1/ x3 ; F4(x) = 1 / (-2x2).
f5(x) =x-½ ; F5(x) =2 x½.
f6(x) = (x+3) /x =1+3 / x ; F6(x) = x+3 ln(x).
2. Calculer les intégrales :
|
|
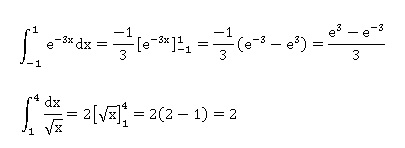
III (3 points)
Vérifier que l'équation (E) : y + y" = 3y5 a pour solution :
y = (cos(2x)-½.
On pose u = cos(2x) ; u' = -2 sin(2x).
y' = sin(2x) [cos(2x)]-1,5.
On pose v = sin(2x) et w = [cos(2x)]-1,5 ; v' = 2 cos(2x) ; w' = 3 sin(2x) [cos(2x)]-2,5.
y" = v'w +v w' = 2 cos(2x) [cos(2x)]-1,5 +3 [sin(2x)]2 [cos(2x)]-2,5.
y"=2 [cos(2x)]-0,5 +3[sin(2x)]2 [cos(2x)]-2,5.
Repport dans (E) :
y + y" = cos(2x)-½+ 2 [cos(2x)]-0,5 +3[sin(2x)]2 [cos(2x)]-2,5.
y + y" =3 [cos(2x)]-0,5+[sin(2x)]2 [cos(2x)]-2,5.].
Or [sin(2x)]2 = 1-[cos(2x)]2 .
y + y" = 3[cos(2x)] -2,5 = 3y5.
|
|
IV. 8 points.
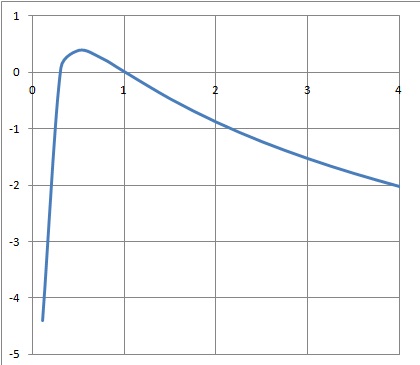
On étudie la fonction d définie sur ]0 ; +oo[ par : f(x) = 1-1 / x -2 ln(x).
1.a. Calculer la dérivée f ' de f.
f '(x) = 1/ x2 -2 /x =(1-2x) / x2.
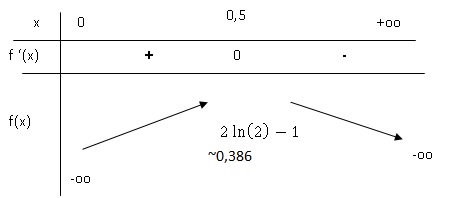
b. Etudier les variations de f.
c. Préciser les limites en zéro et plus l'infini.
Quand x tend vers plus l'infini :
1 /x tend vers zéro ; ln(x) tend vers plus l'infini ; f(x) tend vers moins l'infini.
Quand x tend vers zéro :f(x) =1-[ 1+2x ln(x)] / x.
x ln(x) tend vers zéro ; 1+2x ln(x) / x tend vers plus l'infini ; f(x) tend vers moins l'infini.
2. Montrer que l'équation f(x) = 0 admet exactement deux solutions dont l'une est 1 et l'autre a, est comprise entre 1 /4 et 1 / 3.
Sur [0,5 ; +oo[, f(x) est strictement décroissante
f(0,5)=0,386 ; f tend vers moins l'infini quand x tend vers plus l'infini.
D'après le corollaire du théorème des valeurs intermédiaires, f(x)=0 admet une seule solution sur [0,5 ; +oo[
f(1) = 1-1-2ln(1) = 0 ; cette solution est égale à 1.
Sur ]0 ; 0,5], f(x) est strictement croissante
f(1/4)= -3 + 2 ln(4) ~ -0,227 ;
f(1/3)= -2 + 2 ln(3) ~0,197.
D'après le corollaire du théorème des valeurs intermédiaires, f(x)=0 admet une seule solution sur ]0 ; 0,5].
Cette solution est comprise entre 1 /4 et 1 / 3.
3. Construire la courbe représentative de la fonction f(x).
|
|