Mathématiques,
concours audioprothésiste Nancy 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
I. 3 points.
ABCD est un tétraèdre. Le point P est défini par la relation suivante. Montrer que les points B, P et C sont alignés.
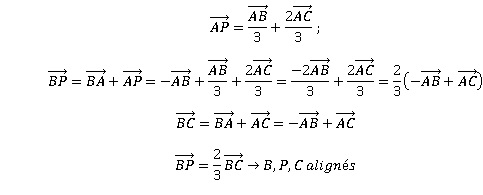
II. 5 points.
Pour tout nombre complexe z on pose : P(z) = z4 +2z3 +11z2 +2z+10.
1. Déterminer deux racines imaginaires pures de l'équation P(z) = 0.
P(i) = i4 +2i3 +11i2 +2i+10 = 1-2i-11+2i+10 =0
P(-i) = (-i)4 +2(-i)3 +11(-i)2 -2i+10 = 1+2i-11-2i+10 =0
2. Achever alors la résolution de P(z)=0.Vitesse à la date t = 50 ms : calcul de la
vitesse moyenne entre 0 et 100 ms.
P(z) =(z-i)(z+i)(z2+bz+c) avec b et c réels.
P(z) =(z2+1) (z2+bz+c)
P(z) = z4 +bz3 +cz2 +z2+bz+c =z4 +2z3 +11z2 +2z+10.
On identifie : c = 10 ; b = 2.
Solutions de z2+2z+10 = 0.
D = 22 -40 = -36 = 36 i2.
z1 = (-2 +6i) / 2 = -1 +3i ; z2 = -1 +3i.
III. 10 points.
Soit la fonction f définie sur R-{-2} par f(x) = (1-x2) / (2+x).
Partie A.
1. Déterminer les trois réels a, b et c tels que : f(x) = ax+b +c /(2+x).
Réduire au même dénominateur : f(x) = [(ax + b ) (2+x)+ c ] / (2+x) =[2ax +ax2 +2b +bx +c] / (2+x).
On identifie : a = -1 ; 2a+b = 0 soit b = 2 ; 2b +c = 1 soit c = -3.
f(x) = -x+2 -3 /(2+x).
2. Calculer :
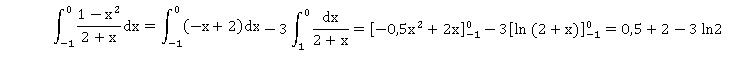
Partie B.
1. Etudier les variations de f et tracer sa courbe représentative C.
On pose u = 1-x2 et v = 2 +x ; u' = -2x ; v' = 1 ;
f '(x) =(u'v +v'u) / v2 = ( -2x(2+x) -(1-x2) ) / (2+x)2 = -( x2+4x+1) / ((2+x)2 .
La dérivée a la signe de -( x2+4x+1).
D = 16-4 = 12 ; x1 =(-4 + 2*3½) / 2 = -2 +3½ et ; x1 =(-4 - 2*3½) / 2 = -2 -3½ .
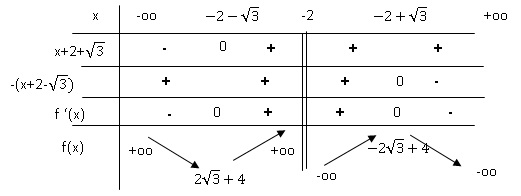
|
|
|
|
|
2. Représenter la droite D d'équation y = -x+2. Préciser les positions relatives de D et C.
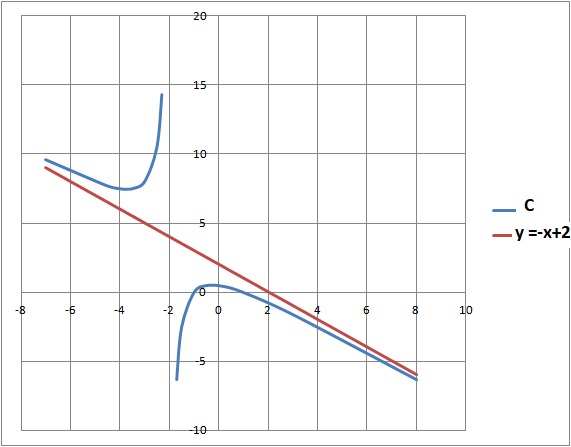
f(x) -( -x+2)= -3 /(2+x).
Si x < -2 ; f(x) -( -x+2) >0 : C au dessus de D.
Si x > -2 ; f(x) -( -x+2) <0 : C au dessous de D.
3. Démontrer que la courbe C admet le point de coordonnées (-2 ; 4) pour centre de symétrie.
On pose X = x+2 et Y = f(x) -4.
f(x) = -x+2-3 /(2+x).
f(x) -4= -x+2-4-3 /(2+x) = -(x+2)-3 /(x+2).
Y = -X -3 / X.
Si on change X en -X, on obtient : X +3 /X = -Y.
|
|
IV. 2 points.
La suite définie par un= e2n+3 est-elle géométrique ?
un= e3 e2n ; un+1= e3 e2(n+1) = e3 e2n+2 =e3 e2n e2= e2 un
u0 =e3 ; (un ) est une suite géométrique de premier terme e3 et de raison e2.
|
|