Modèle de
Bohr, orbite de Hohmann, effet photoélectrique par Millikan,
concours audioprothésiste CNAM 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
I. Modèle de Bohr..
L'atome d'hydrogène est constitué d'un proton de masse m et de charge
e, situé au point O dans un référentiel galiléen et d'un électron en M,
de masse me et de charge -e. Cet électron a un mouvement
circulaire uniforme de centre O, de rayon r et de vitesse v.
L'électron n'est soumis qu'à la force électrostatique attractive du
proton de valeur e2 / (4pe0r2).
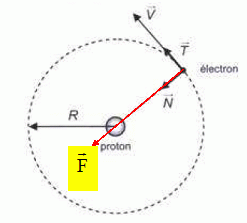
1. Faire un schéma
de l'atome d'hydrogène en faisant figurer la force d'interaction
électrostatique.
 2.
Montrer que mer v2 = e2 /(4pe0).
2.
Montrer que mer v2 = e2 /(4pe0).
L'accélération et la force sont centripètes.
Ecrire la seconde loi de Newton suivant N : e2 / (4pe0r2)
= mev2 / r.
mer v2 = e2
/(4pe0).
3. Dans ce modèle
on a aussi mer v = nh / (2p) où h est la constante de
Plank et n un entier. Exprimer en fonction de n et de certaines
constantes du tableau ci-dessous :
a. La vitesse de
l'électron.
b.
le rayon de sa trajectoire.
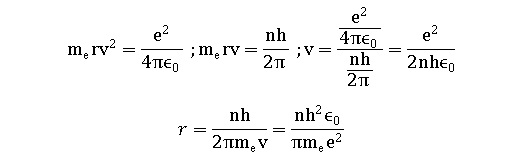
4.
Calculer l'ordre de grandeur du rayon de la trajectooire pour n = 1. Ce
résultat est-il cohérent avec l'ordre de grandeur du rayon atomique ?
r = (6,62 10-34 )2x8,84
10-12 / (3,14 x 9,1 10-31 x(1,6 10-19)2)
~ 5,3 10-11 m ~53 pm.
Ce résultat est cohérent avec l'ordre de
grandeur du rayon atomique
5.
A quelle autre force est soumis l'électron dans l'atome ? A-t-on eu
raison de la négliger ?
L'électron est soumis à son poids P = meg = 9,1 10-31
x9,81 ~9 10-30 N.
Force électrostatique : e2 / (4pe0r2)
= (1,6 10-19)2 / (4 x 3,14 x8,84 10-12
x(5,3 10-11)2) ~ 8 10-8 N.
Le poids est négligeable devant la force électrostatique.
6.
Décrire l'évolution des trajectoires de l'électron quand n augmente,
puis quand n tend vers l'infini. Quel est le sens physique de cette
dernière grandeur ?
r est proportionnel à n ; si n augmente, le rayon de la trajectoire
croît.
Si n tend vers l'infini, l'électron quitte l'atome, ce dernier est
ionisé.
7. L'énergie de l'électron est
quantifiée et vaut En = -13,6 / n2 eV. Expliquer
ce que signifie l'adjectif quantifié.
Toutes les valeurs de l'énergie ne sont pas possible. Seuls un petit
nombre de valeurs sont permises.
8. Un électron
d'énergie E = 10,2 eV vient frapper un atome d'hydrogène d'énergie E1.
a. Sous quelle
forme est l'énergie E= 10,2 eV de l'électron ?
Cette énergie est sous forme cinétique.
b. Quelle est la
valeur du niveau d'énergie E2 dans lequel se retrouve
l'atome après avoir reçu l'énergie de l'électron ?
n = 1 ; E1 = -13,6 eV, état fondamental.
n = 2 ; E2 = -13,6 / 4 = -3,4 eV, premier état excité.
E2-E1 = 10,2 eV.
L'atome se retrouve au prmeir état excité.
9. Dans ce nouvel
état, l'atome est instable et va chercher à retrouver son état de plus
basse énergie. Ce phénomène s'accompagne de l'émission d'un photon.
Déterminer sa fréquence puis sa longueur d'onde. A quel type de
rayonnement appartient ce photon ?
E2-E1 = 10,2 eV. = 10,2 x1,6 10-19 = 1,632 10-18
J.
Fréquence = (E2-E1) / h = 1,632 10-18 / (6,62 10-34)
=2,47 1015 Hz.
Longueur d'onde dans le vide =3,00 108 / (2,47 1015)~1,22 10-7
m =122 nm. Domainr UV.
|
|
II.
Changement d'orbite.
Lors du transfert d'une orbite circulaire de basse
altitude à une orbite circulaire de haute altitude, un satellite
emprunte une orbite dite de " Hohmann". Une telle orbite est élliptique
et a pour foyer le centre de la terre autour de laquelle le satellite
est en révolution. l'orbite a pour périgée un point de l'orbite basse
et pour apogée un point de l'orbite haute.
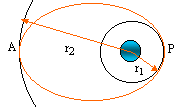
1. Faire un schéma de la situation.
2. Exprimer puis calculer la vitesse
d'un satellite, assimilé à un point matériel :
a. sur une orbite
circulaire basse de 1400 km d'altitude.
v = ( GMterre / (Rterre + h))½ = (6,67
10-11 x 5,98 1024 / (6,36 106 +1,4 106))
=7,17 103 m /s.
b. sur une orbite
circulaire géostationnaire de 36 000 km d'altitude.
v = ( GMterre
/ (Rterre + h))½ = (6,67 10-11 x 5,98
1024 / (6,36 106 +36 106)) =3,07 103
m /s.
3. Calculer le demi-grand axe de
l'orbite de Hohmann correspondant.
a = ½(r1+r2) = 6,36 106 + 0,5( 1,4 106+ 36 106)=2,506 107 ~2,51 107
m.
4. En appliquant la
troisième loi de Kepler, en déduire la durée nécessaire pour faire
passer le satellite de son orbite basse à son orbite haute.
Le
satellite parcourt la moitié de l'ellipse entre A et P. La durée du
parcours est la moitié de la période de révolution T sur l'ellipse. La
troisiéme loi de Kepler donne la période T en fonction de a.
T²
= 4p²
/ (GMterre)
a3.
T
= 2*3,14 x(2,506
107)3
/ (6,67 10-11
x 5,98
1024)
½
=3,95
104
s ; ½T = 1,97 104 s.
|
|
III. Effet photoélectrique par Millikan.
Découvert
par Hertz en 1887, l'effet photoélectrique pose des problèmes
d'interprétation aux physiciens de son époque. Pour Einstein, il y a
émission d'un électron lorsque l'énergie du photon incident est au
minimum égale à l'énergie à fournir à un électron pour qu'il puisse
s'achapper du métal, énergie appelée travail d'extraction.
Lorsque l'énergie du photon est supérieure au travail d'extraction,
l'excès d'énergie est transférée sous forme cinétique à l'électron émis.
Millikan a mis au point une technique expérimentale pour déterminer
l'énergie cinétique maximale des électrons émis par un métal en
fonction de la fréquence des photons incidents, dans le but de montrer
que le raisonnement d'Einstein était faux.
On obtient les résultats suivants pour un métal donné.
Fréquence (THz = 1015 Hz) des photons incidents
|
0,65
|
0,700
|
0,800
|
0,900
|
Ec (eV), énergie cinétique maximale des électrons émis
|
0,50
|
0,69
|
1,10
|
1,52
|
| Ec (aJ=10-18 J), énergie cinétique maximale des électrons émis |
0,08
|
0,11
|
0,176
|
0,243
|
1. Traduire la phrase soulignée par une équation.
Energie du photon- Wextraction = Ec max électrons émis.
h n - Wextraction = Ec max .
h n - hn0 = Ec max
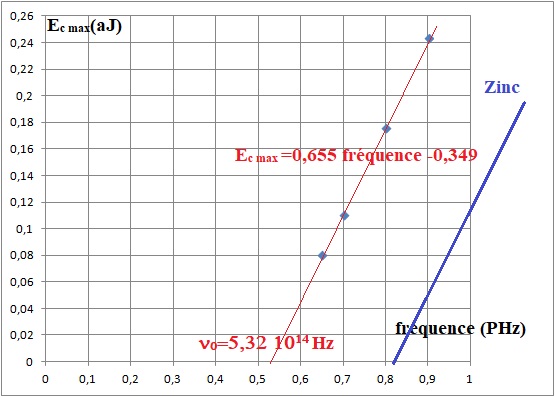
2. Tracer un graphique représentant l'évolution de l'énergie cinétique Ec en fonction de la fréquence..
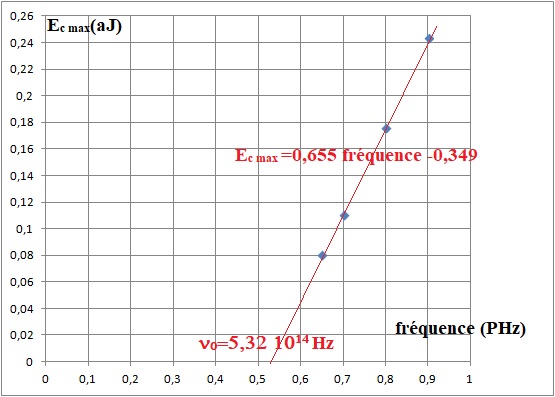
3. Montrer que ces résultats valident le raisonnement d'Einstein et donnent tord à Millikan.
Le graphe est celui d'une fonction affine correspondant à h n - hn0 = Ec max
L'électron n'est émis que lorsque la fréquence du photon incident dépasse une fréquence "seuil" .
4 Déterminer :
a. La fréquence " seuil", la longueur d'onde "seuil" et le travail d'extraction du métal utilisé.
n0 = 0,349 / 0,655 = 0,532 PHz = 5,32 1014 Hz.
Longueur d'onde : 3,00 108 / (5,32 1014) = 5,64 10-7 m.
Travail d'extraction hn0 = 6,62 10-34 x5,32 1014 = 3,52 10-19 J = 2,2 eV.
b. la valeur de la constante de Planck. Cette valeur est-elle en accord avec celle donnée habituellement.
La pente de la droite est égale à h ; graphiquement on trouve 0,655 x 10-18 / 1015 = 0,655 10-33 = 6,55 10-34 J s.
Cette valeur est en accord avec la valeur donnée habituellement 6,62 10-34 J s.
5. Montrer que l'on peut tracer la courbe Ec en fonction de la fréquence d'un autre métal sur le graphique obtenu en connaissant la valeur de sa fréquence seuil.
Ec max=h n - hn0 ; droite de pente h = 6,62 10-34 J s et coupant l'axe des fréquence à la fréquence de seuil n0.
Tracer le grphique réprésentant l'évolution de l'énergie cinétique Ec en fonction de la fréquence pour le zinc dont la fréquence seuil est 8,1 1014 Hz.
|
|