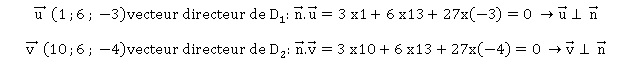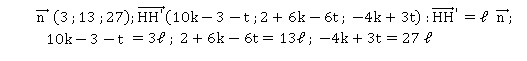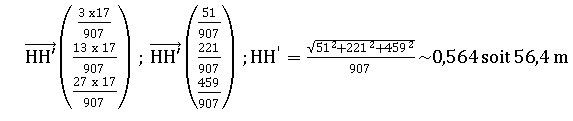Mathématiques, bac S Amérique du sud 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . ...... ..... Exercice 1. 4 points. Partie A. Un commerçant reçoit les résultats d’une étude de marché sur les habitudes des consommateurs en France. Selon cette étude : • 54 % des consommateurs privilégient les produits de fabrication française; • 65 %des consommateurs achètent régulièrement des produits issus de l’agriculture biologique, et parmi eux 72 % privilégient les produits de fabrication française. On choisit un consommateur au hasard. On considère les évènements suivants : • B : « un consommateur achète régulièrement des produits issus de l’agriculture biologique » ; • F : « un consommateur privilégie les produits de fabrication française ». On note P(A) la probabilité de l’évènement A et PC (A) la probabilité de A sachant C. 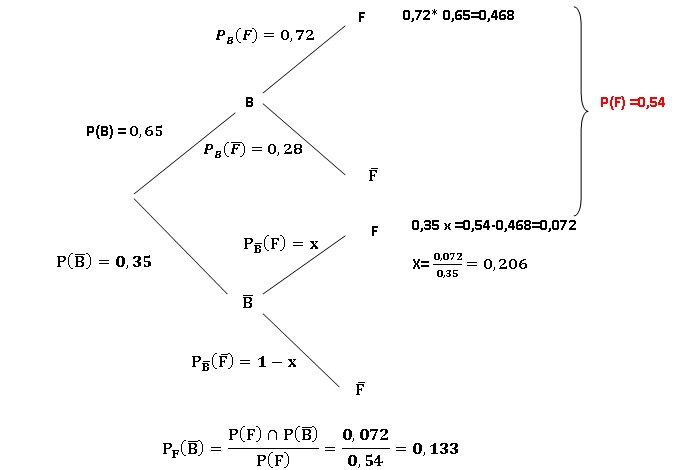1. Justifier que P(non B n F) =0,072. 2. Calculer PF(non B). 3. On choisit un consommateur n’achetant pas régulièrement des produits issus de l’agriculture biologique. Quelle est la probabilité qu’il privilégie les produits de fabrication française ? Partie B. Le commerçant s’intéresse à la quantité en kilogramme de farine biologique vendue chaque mois au détail dans son magasin. Cette quantité est modélisée par une variable aléatoire X qui suit la loi normale d’espérance μ = 90 et d’écart type σ = 2. 1. Au début de chaque mois, le commerçant s’assure d’avoir 95 kg dans son stock. Quelle est la probabilité qu’il ne puisse pas répondre à la demande des clients durant le mois ? P(X >95) =1-P(X < 95) = 1- 0,9938 = 0,0062 ~0,006. 2. Déterminer une valeur approchée au centième du réel a tel que P(X < a) = 0,02. Interpréter le résultat dans le contexte de l’exercice. Exercice 1. 4 points. Partie A. Un commerçant reçoit les résultats d’une étude de marché sur les habitudes des consommateurs en France. Selon cette étude : • 54 % des consommateurs privilégient les produits de fabrication française; • 65 %des consommateurs achètent régulièrement des produits issus de l’agriculture biologique, et parmi eux 72 % privilégient les produits de fabrication française. On choisit un consommateur au hasard. On considère les évènements suivants : • B : « un consommateur achète régulièrement des produits issus de l’agriculture biologique » ; • F : « un consommateur privilégie les produits de fabrication française ». On note P(A) la probabilité de l’évènement A et PC (A) la probabilité de A sachant C. 1. Justifier que P(non B n F) =0,072. 2. Calculer PF(non B). 3. On choisit un consommateur n’achetant pas régulièrement des produits issus de l’agriculture biologique. Quelle est la probabilité qu’il privilégie les produits de fabrication française ? Partie B. Le commerçant s’intéresse à la quantité en kilogramme de farine biologique vendue chaque mois au détail dans son magasin. Cette quantité est modélisée par une variable aléatoire X qui suit la loi normale d’espérance μ = 90 et d’écart type σ = 2. 1. Au début de chaque mois, le commerçant s’assure d’avoir 95 kg dans son stock. Quelle est la probabilité qu’il ne puisse pas répondre à la demande des clients durant le mois ? P(X >95) =1-P(X < 95) = 1- 0,9938 = 0,0062 ~0,006. 2. Déterminer une valeur approchée au centième du réel a tel que P(X < a) = 0,02. Interpréter le résultat dans le contexte de l’exercice. P(X < 85,893) ~ 0,02. La probabilité de vendre moins de 85,893 kg de farine est égale à 0,02. Partie C. Dans cette étude de marché, il est précisé que 46,8 % des consommateurs en France privilégient des produits locaux. Le commerçant constate que parmi ses 2 500 clients, 1 025 achètent régulièrement des produits locaux. Sa clientèle est-elle représentative des consommateurs en France ? On teste l'hypothèse p = 0,468 sur un échantillon de taille n = 2500. n = 2500>30, np = 2500×0,468 = 1170 >5 et n(1−p) = 2500×0,532 = 1330 >5. Les conditions pour établir un intervalle de fluctuation asymptotique au seuil de 95 % sont requises : 1,96 ( p(1-p) / n)½ = 1,96 x(0,468 x0,532/2500)½ =0,0196. Intervalle de fluxtuation : [0,468 -0,0196 ; 0,468 +0,0196] soit [0,448 ; 0,488]. La fréquence 1025 / 2500 = 0,41 n'appartient pas à cet intervalle. Sa clientèle n'est pas représentative des consommateurs en France. Exercice 2. 4 points. Lorsque la queue d’un lézard des murailles casse, elle repousse toute seule en une soixantaine de jours. Lors de la repousse, on modélise la longueur en centimètre de la queue du lézard en fonction du nombre de jours. Cette longueur est modélisée par la fonction f définie sur [0 ; +∞[ par : f (x) = 10eu(x) où u est la fonction définie sur [0 ; +∞[ par :u(x) = −e2− 0,1x. On admet que la fonction f est dérivable sur [0 ; +∞[ et on note f ′ sa fonction dérivée. 1. Vérifier que pour tout x positif on a f ′(x) = −u(x)eu(x). En déduire le sens de variations de la fonction f sur [0 ; +∞[. u'(x) = 0,1e2− 0,1x. f '(x) = u'(x) *10eu(x) =e2− 0,1xeu(x) =−u(x)eu(x). e2− 0,1x et eu(x) sont positifs sur [0 ; +∞[ ; f '(x) est positive et la fonction f(x) est strictement croissante sur cet intervalle. 2. a. Calculer f (20). En déduire une estimation, arrondie au millimètre, de la longueur de la queue du lézard après vingt jours de repousse. u(20) = -e2-2 = -e0 = -1. f(20) = 10 e-1 ~ 3,7 cm. b. Selon cette modélisation, la queue du lézard peut-elle mesurer 11 cm ? Lorsque x tend vers plus l'infini : u(x) tend vers zéro et f(x) tend vers 10 cm. De plus f(x) est strictement croissante ; la queue ne peut pas atteindre 11 cm. 3. On souhaite déterminer au bout de combien de jours la vitesse de croissance est maximale. On admet que la vitesse de croissance au bout de x jours est donnée par f ′(x). On admet que la fonction dérivée f ′ est dérivable sur [0 ; +∞[, on note f ′′ la fonction dérivée de f ′ et on admet que : f "(x) = 0,1 u(x)eu(x)(1+u(x)). a. Déterminer les variations de f ′ sur [0 ; +∞[. u(x) est négatif ; eu(x) est positif ; 1+u(x) =1- e2− 0,1x ; 1+u(x) s'annule pour x = 20. 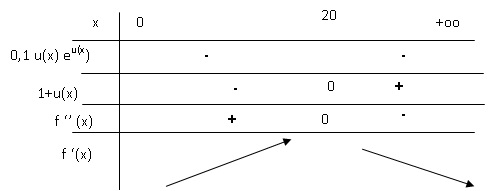b. En déduire au bout de combien de jours la vitesse de croissance de la longueur de la queue du lézard est maximale. La vitesse de croissance de la queue est maximale au bout de 20 jours. ... Exercice 3. 4 points. Deux espèces de tortues endémiques d’une petite île de l’océan pacifique, les tortues vertes et les tortues imbriquées, se retrouvent lors de différents épisodes reproducteurs sur deux des plages de l’île pour pondre. Cette île, étant le point de convergence de nombreuses tortues, des spécialistes ont décidé d’en profiter pour recueillir différentes données sur celles-ci. Ils ont dans un premier temps constaté que les couloirs empruntés dans l’océan par chacune des deux espèces pour arriver sur l’île pouvaient être assimilés à des trajectoires rectilignes. Dans la suite, l’espace est rapporté à un repère orthonormé d’unité 100 mètres. Le plan (O, i, j) représente le niveau de l’eau et on admet qu’un point M(x ; y ; z) avec z < 0 se situe dans l’océan. La modélisation des spécialistes établit que : • la trajectoire empruntée dans l’océan par les tortues vertes a pour support la droite D1 dont une représentation paramétrique est : x = 3+t ; y = 6t ; z = −3t avec t réel. la trajectoire empruntée dans l’océan par les tortues imbriquées a pour support la droite D2 dont une représentation paramétrique est : x = 10k ; y = 2+6k ; z = −4k avec k réel ; 1. Démontrer que les deux espèces ne sont jamais amenées à se croiser avant d’arriver sur l’île. Dans l'hypothèse où les tortues se croisent : 3+t = 10 k soit t = 10 k-3 ; alors y = 60 k-18 différent de 2 +6k. L'hypothèse est fausse ; les tortues ne se croisent pas. 2. L’objectif de cette question est d’estimer la distance minimale séparant ces deux trajectoires. a. Vérifier que le vecteur n de coordonnées ( 3 ; 13 ; 27) est normal aux droites D1 et D2. 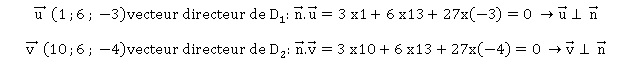b. On admet que la distance minimale entre les droites D1 et D2 est la distance HH′ où le vecteur HH'est un vecteur colinéaire au vecteur n avec H appartenant à la droite D1 et H′ appartenant à la droite D2. Déterminer une valeur arrondie en mètre de cette distance minimale. On pourra utiliser les résultats ci-après fournis par un logiciel de calcul formel H(3+t ; 6t ; -3t ) ; H' (10k ; 2+6k ; -4k). 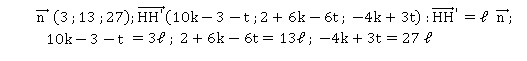Le calcul formel donne la solution. 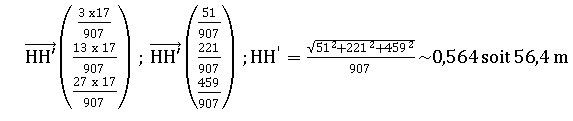3. Les scientifiques décident d’installer une balise en mer. Elle est repérée par le point B de coordonnées (2; 4; 0). a. Soit M un point de la droite D1. Déterminer les coordonnées du point M tel que la distance BM soit minimale. BM = [(3+t-2)2 +(6t-4)2+(-3t)2]½ =[46t2-46t+17]½. La valeur minimale du trinome 46t2-46t+17 est obtenue pour t = 46 / (2 x46) = 0,5. BMmini = (46 x0,25 -46 x0,5 +17)½ =5,5½~2,35 b.En déduire la distance minimale, arrondie au mètre, entre la balise et les tortues vertes. 2,35 x100 = 235 m. .... Exercice 4. 3 points. Le plan est muni d’un repère orthonormal On considère les points A, B, C et D distincts d’affixes respectives zA, zB, zC et zD tels que : zA + zC = zB + zD. zA +izB = zC +izD. Démontrer que le quadrilatère ABCD est un carré. (zA + zC ) / 2 =( zB + zD) / 2 ; {AC] et [BD] se coupent en leur milieu. Le quadrilatère est un parallélogramme. zA-zC = i(zD-zB). Les modules des deux membres donnent : AC = BD. Les arguments des deux membres donnent : les diagonales AC et BD sont perpendiculaires. Les diagonales du parallélogramme ABCD ayant même longueur et étant perpendiculaires, ABCD est un carré. Exercice 5. 5 points. Soit k un réel strictement positif. On considère la suite (un) définie par u0 = 1, u1 = k et, pour tout entier naturel n par : un+2 =u2n+1 / (kun). On admet que tous les termes de la suite (un) existent et sont strictement positifs. 1. Exprimer u2, u3 et u4 en fonction de k. u 2=u21 / (ku0) = k. u 3=u22 / (ku1) = 1. u 4=u23 / (ku2) = 1 /k2. 2. À l’aide d’un tableur, on a calculé les premiers termes de la suite (un) pour deux valeurs de k. La valeur du réel k est entrée dans la cellule E2. 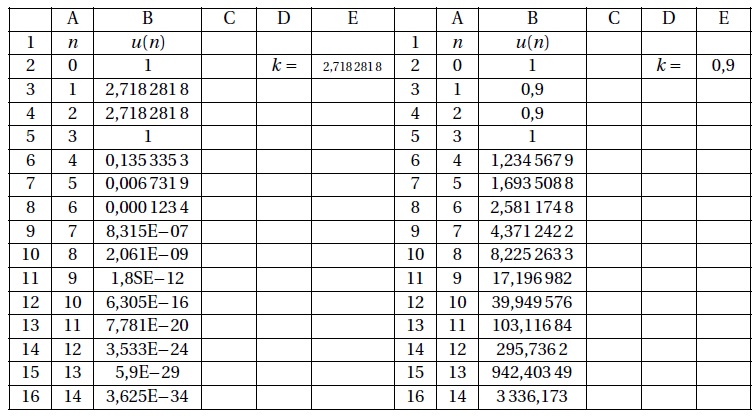a. Quelle formule, saisie dans la cellule B4, permet par recopie vers le bas de calculer tousles termes de la suite (un) ? =B3*B3/($E$2*B2) b. Conjecturer, dans chaque cas, la limite de la suite (un). Si k = 2,7182818, la suite tend vers zéro. Si k = 0,9, la suite tend vers plus l'infini. Dans la suite, on suppose que k =e. On a donc u0 = 1,u1 = e et, pour tout entier naturel n : un+2=u2n+1 / (e un).. 3. On définit, pour tout entier naturel n, la suite (vn) par : vn = ln(un+1)−ln(un). a. Démontrer que la suite (vn) est arithmétique de raison −1 et de premier terme v0 = 1. vn+1 = ln(un+2 / un+1) = ln(un+1/(eun) =ln(un+1) -ln(un) -ln(e) = vn-1. Il s'agit donc d'une suite arithmétique de raison -1. v0 = ln(u1)-ln(u0) = ln(e) -ln(1) = 1. b. En déduire, pour tout entier naturel n,l’expression de vn en fonction de n. vn = v0 +(-1)n = 1-n. 4. On définit, pour tout entier naturel n non nul la suite (Sn) par Sn = v0 +v1+· · ·+vn−1. a. Démontrer que, pour tout entier naturel n non nul, on a Sn =n(3−n) / 2 .Sn =1 +(1-1) +(1-2) +.... +(1-(n-1) = n x1 -(1+2+3+n-1) = n -n(n-1) /2 =n(3-n) / 2. ou bien Sn = n (v0 +vn-1) / 2 = n(1+1-(n-1) / 2 = n(3-n) / 2. b. Démontrer que, pour tout entier naturel n non nul, on a Sn = ln(un). Sn =ln(u1)-ln(u0) + ln(u2)-ln(u1) + ...+ln(un)-ln(un-1) = -ln(u0 + ln(un) = -ln(1) +ln(un) = ln(un). 5. a. Exprimer un en fonction de n et en déduire la limite de la suite (un). ln(un) =n(3-n) / 2 ; un = exp[n(3-n) / 2]. b. Trouver la plus petite valeur de n telle que un < 10−50 par la méthode de votre choix (écriture d’un algorithme, résolution d’inéquation, etc.). exp[n(3-n) / 2] < 10-50 ; n(3-n) < 2 ln(10-50) ; -n2+3n - 2 ln(10-50) < 0 ; On cherche les racines de l'équation : n2-3n + 2 ln(10-50) =0. n2-3n -230,26 ~0 ; D = 9+4 x230,26 ~930,0 ; D½ ~30,5 ; n1 =(3 +30,5) / 2 ~ 16,75 et n2 =(3 -30,5) /  = -13,75. -n2+3n - 2 ln(10-50) < 0 pour n > 17. Avec un algorithme : A <-- 1 ; B <-- e ; N <-- 0 Tant que B > 10-50 C <-- B B <-- B2 / (A) A <-- C N <--N+1 Fin Tant que Afficher N+1.   .

menu