Mathématiques,
Bac STL biotechnologies Métropole 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. (6 points)
Dans cet exercice, les résultats seront arrondis à l’unité, sauf mention contraire.
Cyprien et Cloé, élèves de Terminale STL Biotechnologies, s’intéressent
au protocole d’un examen d’imagerie médicale, qui nécessite de préparer
une dose de produit radioactif. Ils disposent du tableau suivant, qui
donne le nombre de milliards de noyaux radioactifs présents dans le
produit préparé en fonction du temps t , exprimé en minutes.
temps ti (min)
|
0
|
20
|
40
|
60
|
80
|
100
|
120
|
Nombre de noyaux radioactifs ( milliards) yi
|
8000
|
7400
|
6800
|
6300
|
5800
|
5400
|
4900
|
Au
moment de son injection au patient, le produit ne doit pas contenir
plus de 2 600 milliards de noyaux radioactifs. Cyprien et Cloé
souhaitent alors déterminer combien de temps, une fois le produit prêt,
il faut attendre avant de l’injecter au patient.
Partie A.
Cyprien propose d’utiliser un ajustement affine.
1. Représenter le nuage de points de coordonnées (ti , yi ).
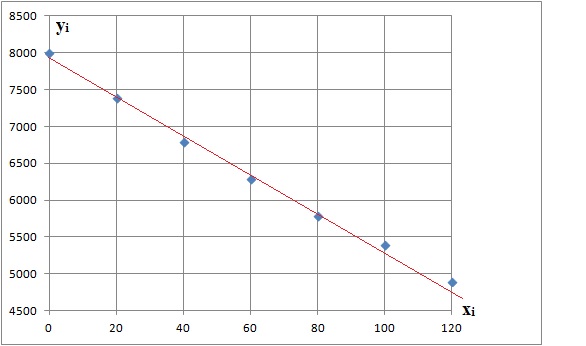
2. Déterminer, à
l’aide de la calculatrice, une équation de la droite d’ajustement de y
en t par la méthode des moindres carrés. On la mettra sous la forme y =
at +b, les réels a et b étant arrondis à 0,1.
y = -25,5 t +7903,6.
3. Cyprien admet
que pendant les quatre heures suivant la préparation du produit, le
nombre y demilliards de noyaux radioactifs encore présents dans le
produit peut être modélisé par y = −26t +7900 où t est le temps,
exprimé en minutes, écoulé depuis que le produit a été préparé.
a. Tracer la droite d d’équation y = −26t +7900 sur le graphique précédent.
b. Cyprien utilise
alors ce modèle pour déterminer, combien de temps, une fois le produit
prêt, il faut attendre avant de l’injecter au patient. Quel temps
Cyprien trouve-t il ?
2600 = -26t +7900 ; 26t = 7900-2600 = 5300 ; t = 5300 / 26 =203,8 minutes = 3 h 24 min.
c. Une nouvelle
mesure est fournie à Cyprien : au bout de 240 minutes, le nombre de
milliards de noyaux radioactifs présents dans le produit préparé est
égal à 3 100. Cette mesure remet-elle en cause le modèle utilisé par
Cyprien ? Pourquoi ?
y = -26 x240 +7900 = 1660, valeur très différente de 3100. Le modèle de Cyprien est remis en cause.
Partie B.
Cloé remet en cause le modèle utilisé par Cyprien. L’examen exploitant
un produit radioactif, elle préfère utiliser un ajustement exponentiel
: le nombre y de milliards de noyaux radioactifs encore présents dans
le produit peut être modélisé par y = A0e−kt où t est le temps, exprimé en minutes,
écoulé depuis que le produit a été préparé, A0 et k étant deux réels strictement positifs.
1. Proposer une démarche qui permette de déterminer des valeurs prises par les réels A0 et k.
A t = 0 : 8000 = A0e−0 ; A0 = 8000.
A t = 240 : 3100 = 8000 exp(-240k) ;
3100 / 8000 =0,3875 = exp(-240k) ;
ln(0,3875) = -240 k ; k = 0,00395.
2. Dans ce qui suit, on prend A0 = 8000 et k = 0,0039.
Cloé utilise alors ce modèle pour déterminer, combien de temps, une
fois le produit prêt, il faut attendre avant de l’injecter au patient.
Quel temps Cloé trouve-t-elle?
2600 = 8000 exp(-0,0039 t) ;
2600 / 8000 =0,325 = exp(-0,0039 t) ; ln0,325 = -0,0039t
t = -ln(0,325) / 0,0039 ~288 minutes.
|
|
|
|
|
Exercice 2. 7 points.
Les deux parties de cet exercice peuvent se traiter de façon indépendante.
Partie A.
En 2017, une étude menée dans une ville a montré que la consommation d’eau par an et par habitant s’élevait à 50 m3. On suppose que, dans les années qui suivront, cette consommation baissera de 2,1% par an.
1. On considère l’algorithme suivant :
n = 0
u = 50
tant que u > 47
u = u x0,979
n = n+1
Fin de tnt que
n = n +2017.
a. Quelle est la valeur de la variable n à la fin de l’exécution de l’algorithme ?
b. Interpréter ce résultat en termes de consommation d’eau par an et par habitant dans cette ville.
50 x 0,979n = 47 ; 0,979n = 47 / 50 ;
n ln(0,979) = ln (47 / 50) ; n = ln (47 / 50) / ln(0,979) = 2,91 soit 3.
3 +2017 = 2020.
2. On modélise la situation par une suite (un) où un représente la consommation d’eau, en m3, par an et par habitant, dans cette ville en 2017+n.
a. Montrer que la suite (un) est géométrique. Préciser son premier terme et sa raison.
On passe d'un terme au suivant en le multipliant par 0,979 ; il s'agit
d'une suite géométrique de raison 0,979 et de premier terme u0 = 50.
b. Exprimer, pour tout entier naturel n, un en fonction de n.
un = 50 x0,979n.
c. Avec ce modèle, quelle consommation d’eau peut-on prévoir par an et par habitant en 2021? On arrondira à 0,1m3.
n= 4 ; u4 = 50 x0,9794 ~45,9 m3.
3. On s’intéresse à la consommation totale d’eau par habitant depuis le début de l’année 2017.
Déterminer à partir de quelle année cette consommation totale d’eau dépassera 500 m3.
Somme des termes de la suite : S = u0(1-qn+1) /(1-q) ;
50(1-0,979n+1) / 0,021 > 500 ; 1-0,979n+1 >0,21 ; 0,979n+1 < 1-0,21 ; 0,979n+1 < 0,79.
n ln(0,979) < ln(0,79) ; n > 11,1.
A partir de l'année 2017 +12 = 2029, la consommation totale d'eau dépassera 500 m3.
Partie B.
Dans cette partie, les probabilités demandées seront arrondies à 10−4.
On
sait qu’en 2017, 37% des logements de la ville étaient équipés de
systèmes de réduction de la consommation d’eau (robinets mousseurs,
récupérateurs d’eau de pluie, . . . ).
1.
On considère un échantillon de 1 000 logements pris au hasard parmi les
logements de la ville, suffisamment nombreux pour assimiler le choix de
cet échantillon à un tirage avec remise. On note X la variable
aléatoire égale au nombre de logements de l’échantillon qui étaient
équipés de systèmes de réduction de la consommation d’eau en 2017.
a. Déterminer la loi suivie par la variable aléatoire X. Préciser les paramètres de cette loi.
Les
prélevements sont indépendants, deux issues sont possibles et leur
nombre est fixé à n = 1000. La probabilité qu'un logement soit
équipé est constante p = 0,37. La probabilité qu'un
logement ne soit pas équipé est q =1-p =0,63.
X suit la loi binomiale de paramètre n = 1000 et p = 0,37.
b.
Quelle est la probabilité qu’il y ait plus de 400 logements dans
l’échantillon qui étaient équipés de tels systèmes de réduction de la
consommation d’eau en 2017 ?
P(X > 400) = 1 -P(X < 400) = 1-0,9797 =0,0233
2. On décide d’approcher la variable aléatoire X par une variable aléatoire Y qui suit la loi normale de paramètres μ= 370 et �s= 15,27.
a. Justifier les valeurs choisies pour μ et �s.
Espérance = np = 1000 x0,37 = 370 ; écart type = (n p(1-p))½=(1000 x0,37 x0,63)½ =15,27.
b. Calculer la probabilité P(Y < 350). Interpréter le résultat obtenu dans le contexte.
P(Y < 350) =0,0951.
La probabilité que moins de 350 logements soient équipés est égale à 0,0951.
.
|
|
Exercice 3.
7 points.
Les deux parties de cet exercice sont indépendantes.
Un antibiotique est une substance chimique organique inhibant ou tuant des bactéries pathogènes.
Partie A.
Un laboratoire affirme que 48% de toutes les souches bactériennes sont résistantes aux antibiotiques.
Dans un échantillon de 50 souches bactériennes prises au hasard, on
constate que 29 souches sont résistantes. Cela remet-il en cause
l’affirmation du laboratoire? Justifier.
n = 50 > 30 ; np = 50 x0,48 = 24 > 5 ; n(1-p) = 50 x0,52 = 26 > 5.
Les conditions sont requises pour définir un intervalle de fluctuation au seuil de confiance de 95 %.
1,96(p(1-p) / n)½ = 1,96 (0,48 x0,52 / 50)½ = 0,138.
[0,48-0,138 ; 0,48 +0,138 ] soit [0,342 ; 0,618 ).
29 / 50 = 0,58 appartient à cet intervalle. l'affirmation n'est pas remise en cause.
Partie B
On injecte un antibiotique à un patient. On modélise cette situation
par une fonction f qui, à tout temps t , exprimé en heures, écoulé
depuis l’injection, associe la concentration, exprimée en mg·L−1, de l’antibiotique dans le sang du patient.
Cette fonction f est définie sur l’intervalle [0,+∞[ par
f (t ) = 8t / (t2+1).
1. On admet que la limite de la fonction f en +∞est égale à 0.
a. Interpréter la valeur de la limite pour la courbe représentative de la fonction f .
L'axe des abscisses est asymptote à la courbe.
b. Interpréter la valeur de la limite dans le contexte de l’exercice.
Au bout d'un temps suffisamment long, la concentration de l'antibiotique dans le sang est nulle.
2. On note f ′ la fonction dérivée de la fonction f .
a. On admet que pour tout réel t positif ou nul, on a : f ′(t )= 8(1-t)(1+t) / (t2+1)2.
Étudier le signe de f ′ sur [0 , +∞[ et en déduire le tableau de variations de f .
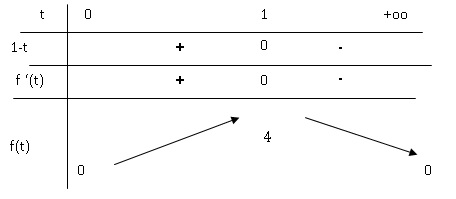
b. Au bout de
combien de temps après l’injection la concentration de l’antibiotique
est elle maximale ? Préciser cette concentration maximale en mg·L−1.
Au bout d'une heure, la concentration est maximale et vaut 4 mg / L.
3. En
antibiothérapie, on définit la CMI comme la concentration minimale
d’antibiotique permettant d’empêcher la multiplication bactérienne. La
CMI de l’antibiotique injecté est égale à 2,4 mg·L−1.
a. Montrer que, pour tout réel t positif ou nul, f (t )−2,4 =(−2,4t 2 +8t −2,4) / (t 2 +1)
.f (t )−2,4 =8t / (t2+1) -2,4 = [8t -2,4(t2+1)] / (t2+1)=(−2,4t 2 +8t −2,4) / (t 2 +1).
b. Étudier le signe de cette expression sur l’intervalle [0 , +∞[.
Le signe de cette expression est celui de −2,4t 2 +8t −2,4.
On cherche les solutions de 2,4t 2 -8t +2,4 = 0.
D = (-8)2 -4 x2,4 x2,4 = 40,96 ; x1 = (8-6,4) / 4,8 = 1 / 3 ; x2 = (8+6,4) / 4,8 =3.
f(t)-2,4 est positive sur l'intervalle [1 /3 ; 3 ].
f(t)-2,4 est nulle pour t = 1 /3 et t = 3.
f(t) est négative pour t appartenant à [0 ; 1 / 3] et [3 ; +oo [.
c. Montrer que la concentration de l’antibiotique injecté est supérieure à sa CMI pendant 2 h 40.
3 - 1 /3 = 9 /3 -1 /3 = 8 /3 heures ou 2 h 40 min.
4. a. Vérifier que la fonction F définie sur [0 , +∞[ par F(t ) = 4ln(t 2 +1) est une primitive de f sur cet intervalle.
Dériver F(t) en posant u = (t2+1) ; u' = 2t.
F '(t) = 8t / (1+t2)= f(t).
b. En déduire la valeur exacte de l’intégrale J =F(12) -F(0).
J = 4 ln(122 +1) -4 ln (1) = 4 ln(145).
c. On admet que la valeur moyenne de la concentration de l’antibiotique en mg·L−1 durant les douze premières heures après l’injection est égale à
J / 12. Déterminer cette valeur moyenne, arrondie au centième de mg·L−1.
4 ln(145) / 12 ~ 1,66 mg / L.
|
|