Mathématiques,
fonction, probabilités, suites, géométrie,
Bac S Métropole 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1. 4 points.
Une
étude statistique a été menée dans une grande ville de France entre le
1er janvier 2000 et le 1er janvier 2010 afin d’évaluer la proportion
des ménages possédant une connexion internet fixe. Au 1er janvier 2000,
un ménage sur huit était équipé d’une connexion internet fixe et, au
1er janvier 2010, 64% des ménages l’étaient. Suite à cette étude, cette
proportion a été modélisée par la fonction g définie sur l’intervalle
[0 ; +∞[ par :
g (t ) =1/(1+ke−at ),
où k et a sont deux constantes réelles positives et la variable t
désigne le temps, compté en années, écoulé depuis le 1er janvier 2000.
1. Déterminer les valeurs exactes de k et de a pour que g (0)=1 / 8 et g (10) = 64 / 100.
1 / 8 = 1 /(1+k) ; 1+k = 8 ; k = 7.
64 / 100 = 1 /(1+7 e-10a) ; 1+7 e-10a =100 / 64 ; 7 e-10a = 36 / 64 ;
-10a = ln(36 / (64 x7)) ~-2,52 ; a ~ 0,25.
2. Dans la suite, on prendra k = 7 et a = 0,25. La fonction g est donc définie par :
g (t )=1 / (1+7e−0,25t)
a. Montrer que la fonction g est croissante sur l’intervalle [0 ; +∞[.
On pose u = 1+7e−0,25t ; u' = -7 x0,25 e−0,25t = -1,75 e−0,25t ;
g(u) = 1 / u ; g'(u) = -u' / u2 = 1,75 e−0,25t / (1+7e−0,25t)2.
Le terme en exponentielle étant toujours positif, la dérivée est positive ; g(t) est strictement croissante sur [0 ; +∞[.
b.
Selon cette modélisation, peut-on affirmer qu’un jour, au moins 99% des
ménages de cette ville seront équipés d’une connexion internet fixe?
Justifier la réponse.
Quand t tend vers plus l'infini, e−0,25t tend vers zéro ; g(t) tend vers 1 (100 %).
Un jour, au moins 99% des ménages de cette ville seront équipés d’une connexion internet fixe.
3. a.
Donner, au centième près, la proportion de foyers, prévue par le
modèle, équipés d’une connexion internet fixe au 1er janvier 2018.
t = 18 ; g(18) = 1 / (1+7 e-18 x0,25) =0,93.
b. Compte tenu du
développement de la téléphonie mobile, certains statisticiens pensent
que la modélisation par la fonction g de l’évolution de la proportion
de ménages possédant une connexion internet fixe doit être remise en
cause.
Au début de l’année 2018 un sondage a été effectué. Sur 1 000 foyers, 880 étaient équipés d’une connexion fixe.
Ce sondage donne-t-il raison à ces statisticiens sceptiques ?
(On pourra utiliser un intervalle de fluctuation asymptotique au seuil de 95%.)
n = 1000 ; p = 0,93 ; 1,96[p(1-p) / n] ½ =1,96[0,93 x0,07 / 1000] ½ =0,016.
Intervalle de fluctuation asymptotique : [0,93-0,016 ; 0,93 +0,016] soit [ 0,914 ; 0,946 ].
880 / 1000 = 0,88, cette valeur est plus petite que la borne inférieure de l'intervalle. Ce sondage donne raison à ces statisticiens sceptiques.
Exercice 2. 5 points.
Le plan complexe est rapporté à un repère orthonormé direct. On prendra pour unité graphique le centimètre.
1. Résoudre dans C l’équation
(z2−2z +4)(z2+4)=0.
z2+4 = 0 ; z2 = -4 = 4 i2 ; z = ±2i.
z2−2z +4= 0 ; D = (-2)2 -4 x4 = -12 = 12 i2 = (±2 *3½i)2.
Solutions :(2 + 2 *3½i) / 2 = 1 +3½i et 1-3½i.
2. On considère les points A et B d’affixes respectives zA = 1+i3½ et zB = 2i.
a. Écrire zA et zB sous forme exponentielle et justifier que les points A et B sont sur un cercle de centre O dont on précisera le rayon.
|zA| =(1+3)½ = 2 ; zA /|zA| =0,5(1+i3½ ) =cos (p/3)+ isin (p/3) ; zA = 2 eip/3.
zB = 2 eip/2.
OA = OB = 2.
Les points A et B sont sur un cercle de centre O et de rayon R = 2
b. Faire une figure et placer les points A et B.
c. Déterminer une mesure de l’angle (AOB).
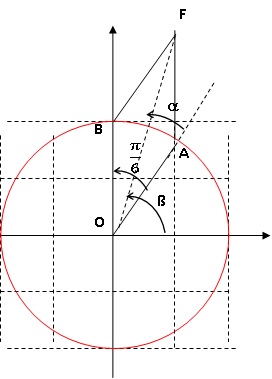
3. On note F le point d’affixe zF = zA +zB.
a. Placer le point F sur la figure précédente.Montrer que OAFB est un losange.
zF = zA +zB =1 + i(2+3½).
AF = [02+22 ]½ =2 = OA = OB.
BF = [12+(3½)2 ]½ =2 = OA = OB.
Les quatre cotés du quadrilatère OAFB sont égaux.
De plus zA-zO = 1+i3½ et zF-zB = 1+i3½ ; zA-zO =zF-zB, le quadrilatère est un parallélogramme ayant deux cotés consécutifs égaux, c'est donc un losange..
b. En déduire une mesure des angles a et ß.
Les diagonales d'un losange sont perpendiculaires et axes de symétrie de la figure.
a = p /12 et ß = p /3 + p /12 =5 p /12.
c. Calculer le module de zF et en déduire l’écriture de zF sous forme trigonométrique.
zF =1 + i(2+3½) ; | zF | =[ 12 + (2+3½)2]½=2(2+3½)½.
zF =2(2+3½)½( cos(5 p /12) + i sin(5 p /12)).
d. En déduire la valeur exacte de cos(5 p /12).
2(2+3½)½( cos(5 p /12) + i sin(5 p /12)) = 1 + i(2+3½).
On identifie les parties réelles :
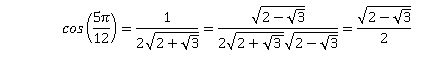 .
.
4. Deux modèles de calculatrice de marques différentes donnent :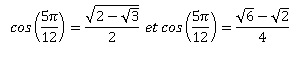
Ces résultats sont-ils contradictoires ? Justifier la réponse.
Ces résultats ne sont pas contradictoires.
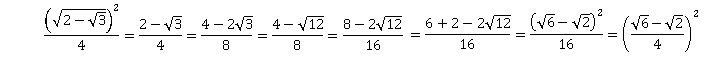
|
|
Exercice 3. QCM. 6 points.
Cet exercice est un QCM (questionnaire à choix multiple). Pour chaque
question, quatre réponses sont proposées et une seule d’entre elles est
exacte.
Le candidat indiquera sur la copie le numéro de la question suivi de la réponse choisie.
Aucune justification n’est demandée.
Il est attribué 1,5 point par réponse correcte.
Aucun point n’est enlevé en l’absence de réponse ou en cas de réponse incorrecte.
Question 1.
Dans l’espace rapporté à un repère orthonormé on considère la droite (D) de représentation
paramétrique
x = 2+ t
y = 1−3t
z = 2t
(t ∈ R), et le plan (P) d’équation cartésienne x+y+z−3 = 0.
On peut affirmer que :
Réponse A : la droite (D) et le plan (P) sont strictement parallèles.
Réponse B : la droite (D) est incluse dans le plan (P). Vrai.
Réponse C : la droite (D) et le plan (P) se coupent au point de coordonnées (4 ; −5 ; 4).
Réponse D : la droite (D) et le plan (P) sont orthogonaux.
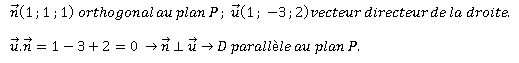
A(2 ; 1 ; 0) appartient à la droite D et au plan P.
Question 2.
Dans le rayon informatique d’une grande surface, un seul vendeur est présent et les clients sont nombreux.
On admet que la variable aléatoire T , qui, à chaque client, associe le
temps d’attente en minutes pour que le vendeur soit disponible, suit
une loi exponentielle de paramètre λ.
Le temps d’attente moyen est de 20 minutes.
Sachant qu’un client a déjà attendu 20 minutes, la probabilité que son attente totale dépasse une demi-heure est :
Réponse A : e−0,5. Vrai.
Réponse B : e−1,5.
Réponse C : 1−e−0,5
Réponse D : 1−e−10λ.
l =1 / 20 =0,05.
P20(T >30) = P(T > 10) = e-0,05 x10 =e−0,5.
Question 3.
Une usine fabrique des balles de tennis en grande quantité. Pour être
conforme au règlement des compétitions internationales, le diamètre
d’une balle doit être compris entre 63,5 mm et 66,7 mm.
On note D la variable aléatoire qui, à chaque balle produite, associe son diamètre mesuré en millimètres.
On admet que D suit une loi normale de moyenne 65,1 et d’écart type σ.
On appelle P la probabilité qu’une balle choisie au hasard dans la production totale soit conforme.
L’usine décide de régler les machines de sorte que P soit égale à 0,99.
La valeur de σ, arrondie au centième, permettant d’atteindre cet
objectif est :
Réponse A : 0,69 ; Réponse B : 2,58 ; Réponse C : 0,62 ; Vrai ; Réponse D : 0,80.
On pose Z =( D-65,1) / s ; P(63,5-65,1) / s < Z < ( 66,7-65,1) / s ) = 0,99.
P(-1,6 / s < Z ) = 0,0005. s = 0,62.
Question 4.
La courbe ci-dessous est la représentation graphique, dans un repère orthonormé, de la fonction f définie par : f(x) = 4 x / (x2+1).
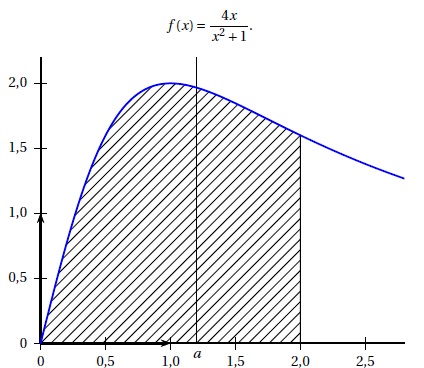
La valeur exacte du réel positif a tel que la droite d’équation x = a
partage le domaine hachuré en deux domaines d’aires égales est :
Réponse A : 1,50,25 ; Réponse B :( 5½-1)½ Vrai ; Réponse C : ln5−0,5 ; Réponse D : 10 / 9.
On pose u = x2+1 ; u' = 2x ; f(u) = 2u' / u. Primitive de f(x) : F(x)= 2 ln(x2+1).
Aire hachurée : F(2) -F(0) = 2 ln(5)-2 ln(1) = 2 ln(5).
F(a)-F(0) = ln(5) ;
2 ln(a2+1) = ln(5) ; (a2+1)2 = 5 ; a2+1 = 5½ ; a2 = 5½ -1.
|
|
Exercice 4. 5 points.
On considère la fonction f définie sur R par :
f (x) =0,5 x2 -x +1,5
Soit a un réel positif.
On définit la suite (un) par u0 = a et, pour tout entier naturel n : un+1 = f (un).
Le but de cet exercice est d’étudier le comportement de la suite (un) lorsque n tend vers +∞, suivant différentes valeurs de son premier terme u0 = a.
1. À l’aide de la calculatrice, conjecturer le comportement de la suite (un) lorsque n tend vers +∞, pour a = 2,9 puis pour a = 3,1.
Si u0 = 2,9 la suite tend vers 1.
Si u0 = 3,1 la suite tend vers plus l'infini.
2. Dans cette question, on suppose que la suite (un) converge vers un réel ℓ.
a. En remarquant que un+1 =0,5un2-un+1,5 ,montrer que ℓ =0,5ℓ 2-ℓ+1,5.
La suite converge vers l et la fonction f(x) est continue en l.
un+1 = f(un) tend vers l quand n tend vers plus l'infini.
D'autre part un+1 tend vers l quand n tend vers plus l'infini.
Par passage à la limite : l = f(l).
b. Montrer que les valeurs possibles de ℓ sont 1 et 3.
0,5ℓ 2-2ℓ+1,5 =0 ; D = 4 -4 x 0,5 x1,5 = 1.
Solutions : (2 ±1) / 1 = 2 ±1 soit 1 et 3.
3. Dans cette question, on prend a = 2,9.
a. Montrer que f est croissante sur l’intervalle [1 ; +∞[.
f '(x) = x-1.
f '(x) est positive sur [1 ; +∞[. Donc f(x) est croissante sur cet intervalle.
b. Montrer par récurrence que, pour tout entier naturel n, on a : 1 < un+1 < un.
Initialisation : u0 = 2,9 ; u1 = 2,805, la propriété est vraie au rang 1.
Hérédité : on suppose que la propriété est vraie au rang n. 1 < un+1 < un.
La fonction f étant croissante sur [1 ; +∞[, un et un+1 appartiennent à cet intervalle donc f(un) > f(un+1), c'est à dire un+1 > un+2.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier n.
c. Montrer que (un) converge et déterminer sa limite.
La suite est décroissante et bornée, donc elle converge.
La limite de la suite est l = 1.
4. Dans cette question, on prend a = 3,1 et on admet que la suite (un) est croissante.
a. À l’aide des questions précédentes montrer que la suite (un) n’est pas majorée.
Hypothèse : la suite est majorée par M signifie qu'elle converge vers 1 ou vers 3.
Or u0 > 3. La suite étant croissante, elle ne peut pas converger vers 1 ou 3.
L'hypoyhèse est donc fausse. La suite n'est pas majorée.
b. En déduire le comportement de la suite (un) lorsque n tend vers +∞.
Quand n tend vers plus l'infini, une suite croissante non majorée tend vers plus l'infini.
c. L’algorithme suivant calcule le plus petit rang p pour lequel up > 106.
Recopier et compléter cet algorithme.
P est un nombre entier et U est un nombre réel.
P <--- 0
U <---3,1
Tant que U < 106
P <---P+1
U <---0,5 xU2 -U +1,5
Fin de Tant que.
|
|