Mathématiques,
tétraèdre, nombres complexes,
Bac S Asie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
3.
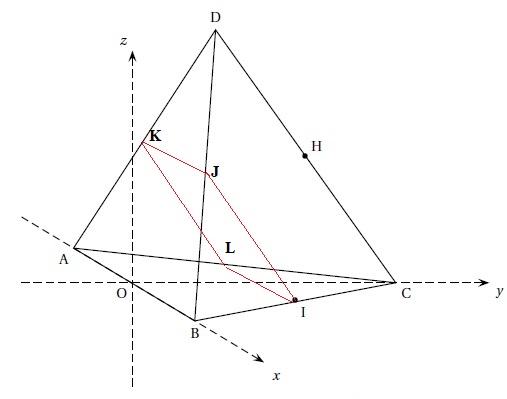
On se place dans un repère orthonormé d’origine O et d’axes (Ox), (Oy) et (Oz).
Dans ce repère, on donne les points A(−3 ; 0 ; 0), B(3; 0; 0) , C(0 ; 3 *3½ ; 0) et D(0 ; 3½ ; 2*6½).
On note H le milieu du segment [CD] et I le milieu du segment [BC].
1. Calculer les longueurs AB et AD.
AB =[ ( 3-(-3))2 +(0-0)2 +(0-0)2 ]½ = 6.
AD =[ ( 0-(-3))2 +(3½-0)2 +(2*6½-0)2 ]½ = 6.
On
admet pour la suite que toutes les arêtes du solide ABCD ont la même
longueur, c’est-à-dire que le tétraèdre ABCD est un tétraèdre régulier.
On appelle P le plan de vecteur normal OH et passant par le point I.
2. Étude de la section du tétraèdre ABCD par le plan P
a. Montrer qu’une équation cartésienne du plan P est : 2y3½+z6½−9= 0.
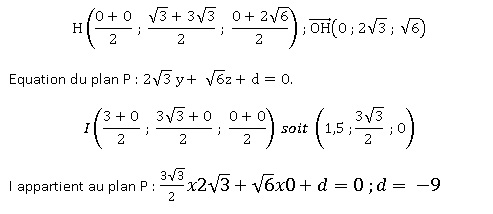
b. Démontrer que le milieu J de [BD] est le point d’intersection de la droite (BD) et du plan P .
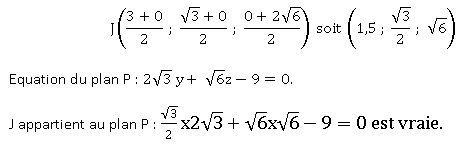
J est donc l'intersection du plan P et de la droite (BD).
c. Donner une
représentation paramétrique de la droite (AD), puis démontrer que le
plans P et la droite (AD) sont sécants en un point K dont on
déterminera les coordonnées.

d. Démontrer que les droites (IJ) et (JK) sont perpendiculaires.
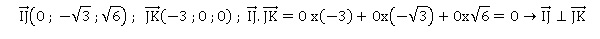
e. Déterminer précisément la nature de la section du tétraèdre ABCD par le plan P .
On appelle L le milieu du segment [AC] ; coordonnées de L :( -1,5 ; 1,5 *3½ ; 0)
Montrons que L appartient au plan P : 2*3½ *1,5*3½ +6½*0 -9 = 0 est vraie.
L appartient donc au plan P .
Le plan P coupe donc [BC] en I, [BD] en J, [AD] en K et [AC] en L : donc la section du tétraèdre ABCD
par le plan P est le quadrilatère (IJKL).
Dans le triangle (BCD), (IJ) // (CD) (droite des milieux) et CD = 2IJ = 6 soit IJ = 3,
Dans le triangle (ACD), (KL) // (CD) (droite des milieux) et CD = 2KL = 6 soit KL= 3,
Dans le triangle (ABC), (IL) // (AB) (droite des milieux) et AB = 2IL = 6 soit IL = 3.,
Dans le triangle (ABD), (JK) // (AB) (droite des milieux) et AB = 2JK = 6 soit JK = 3.
Par suite IJ = JK = KL = LI = 3, donc le quadrilatère (IJKL) est un losange.
Or on a démontré à la question 2. d. que les droites (IJ) et (JK) sont perpendiculaires, donc (IJKL) est un carré.
3. Peut-on placer un point M sur l’arête [BD] tel que le triangle OIM soit rectangle en M ?
Equation paramétrique de la droite (BD) :

|
|
Exercice 4.
Dans cet exercice, x et y sont des nombres réels supérieurs à 1.
Dans le plan complexe muni d’un repère orthonormé direct, on considère les points A, B et C d’affixes respectives
zA = 1+i, zB = x +i et zC = y +i.

1. Démontrer que si OC =OA×OB, alors y2 = 2x2 +1.
OC = (y2 +12)½ ; OA = (12 +12)½ =2½ ; OB = (x2 +12)½ ;
OA x OB = 2½ (x2 +12)½ = (2x2 +1)½ ;
(y2 +12)½ = (2x2 +2)½ soit y2 +1 =2x2 +1 ; y2 = 2x2 +1.
2. Reproduire sur la copie et compléter l’algorithme ci-après pour qu’il affiche tous les couples (x, y) tels que :
y2 = 2x2 +1.
x et y sont des nombres entiers
1< x <10 et 1< y <10
Pour x allant de 1 à 10 faire
Pour y allant de 1 à 10 faire
Si y2 = 2x2 +1
Afficher x et y
Fin Si
Fin Pour
Fin Pour
Lorsque l’on exécute cet algorithme, il affiche la valeur 2 pour la variable x et la valeur 3 pour la variable y.
3. Étude d’un cas particulier : dans cette question seulement, on prend x = 2 et y = 3.
a. Donner le module et un argument de zA.
|zA|=(12+12)½ = 2½.
zA / |zA|=1 / 2½ + i / 2½ = cos (p/4) + i sin (p/4).
b. Montrer que OC =OA×OB.
y2 =9 ; 2x2 +1 =8+1 = 9 ; donc y2 = 2x2 +1 ; par suite OC =OA×OB.
c. Montrer que zBzC = 5zA et en déduire la relation suivante.
zBzC =(2+i)(3+i) = 6+i2+5i =5(1+i) = 5 zA.
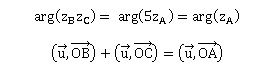
|
|
4.
On revient au cas général, et on cherche s’il existe d’autres valeurs
des réels x et y telles que les points A, B et C vérifient les deux
conditions données ci-dessus.
a. Démontrer que arg·[(x +i)(y +i) / (1+i) ]=0 mod 2p.
En déduire que sous cette condition : x + y −xy +1 = 0.
arg·[(x +i)(y +i) / (1+i) ] = arg(zB) +arg(zC) -arg(zA).
Or arg(zB) +arg(zC) =arg(zA).
Donc arg·[(x +i)(y +i) / (1+i) ]=0 mod 2p.
(x +i)(y +i) / (1+i) =[xy +i2+i(x+y)] / (1+i)
[xy-1+i(x+y)](1-i) / 2 = [xy-1+x+y +i(x+y-xy+1)] / 2.
Or arg·[(x +i)(y +i) / (1+i) ]=0, donc x+y-xy+1 = 0.
b. Démontrer que si les deux conditions sont vérifiées et que de plus x diffère de1, alors :
y =(2x2+1)½ et y = (x+1) / (x-1).
D'une part : y2 = 2x2 +1 soit y =(2x2+1)½ ;
D'autre part : x+y-xy+1 = 0 ; y(1-x) +x+1) = 0 ; y= (x+1) / (x-1).
5. On définit les fonctions f et g sur l’intervalle ]1 ; +∞[ par :
f (x) =(2x2+1)½ et g (x)= (x+1) / (x-1).
Déterminer le nombre de solutions du problème initial.
On pourra utiliser la fonction h définie sur l’intervalle ]1 ; +∞[ par
h(x) = f (x)− g (x) et s’appuyer sur la copie d’écran d’un logiciel de
calcul formel donnée ci-dessous.

Sur l’intervalle ]1 ; +∞[ :
la dérivée de f(x) est positive, f(x) est strictement croissante ;
la dérivée de g(x) est négative, la fonction g(x) est strictement décroissante.
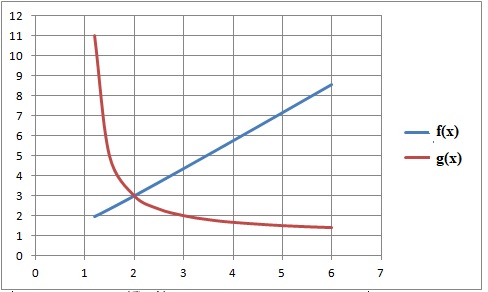
Le problème a une seule solution.
|
|