Mathématiques,
fonction, probabilités,
Bac S Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
La
municipalité d’une grande ville dispose d’un stock de DVD qu’elle
propose en location aux usagers des différentes médiathèques de cette
ville.
Afin de renouveler son offre de location, la municipalité décide de retirer des DVD de son stock.
Parmi les DVD retirés, certains sont défectueux, d’autres non.
Parmi les 6% de DVD défectueux sur l’ensemble du stock, 98% sont retirés.
On admet par ailleurs que parmi les DVD non défectueux, 92% sont maintenus dans le stock ; les autres sont retirés.
Les trois parties sont indépendantes.
Partie A.
On choisit un DVD au hasard dans le stock de la municipalité.
On considère les événements suivants :
• D : « le DVD est défectueux » ;
• R : « le DVD est retiré du stock ».
1. Démontrer que la probabilité de l’événement R est 0,134.
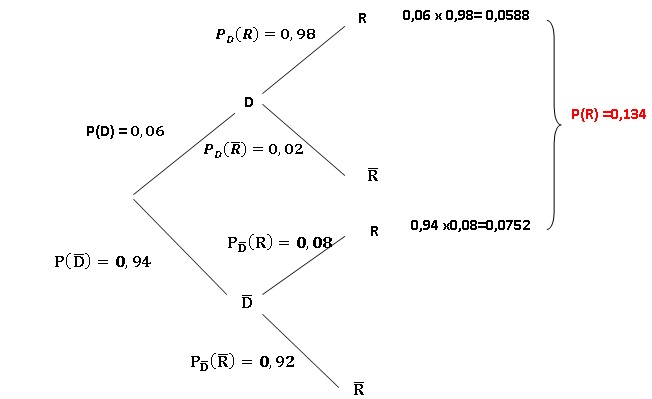
2. Une association
caritative contacte la municipalité dans l’objectif de récupérer
l’ensemble des DVD qui sont retirés du stock. Un responsable de la
ville affirme alors que parmi ces DVD retirés, plus de lamoitié est
composée de DVD défectueux.
Cette affirmation est-elle vraie ?
probabilité de l'évènement " le DVD est défectueux sachant qu'il est retiré".
PR(D) = P(R n D) / P(R) =0,0588 / 0,134 = 0,439, valeur inférieure à 0,5.
L'affirmation est fausse.
Partie B.
Une des médiathèques de la ville se demande si le nombre de DVD
défectueux qu’elle possède n’est pas anormalement élevé. Pour cela,
elle effectue des tests sur un échantillon de 150 DVD de son propre
stock qui est suffisamment important pour que cet échantillon soit
assimilé à un tirage successif avec remise. Sur cet échantillon, on
détecte 14 DVD défectueux.
Peut-on rejeter l’hypothèse selon laquelle, dans cette médiathèque, 6% des DVD sont défectueux ?
n = 150 > 30 ; np = 150 x0,06 = 9 > 5 ; n(1-p) = 150 x0,94 =141 > 5.
Les conditions sont réunies pour définir un intervalle de fluctuation
au seuil de 95 %.
1,96 [(p(1-p) / n]½
= 1,96 x[0,06 x0,94 / 150]½ = 0,038.
I = [0,06-0,038 ; 0,06 +0,038] soit [0,022 ; 0,098].
La fréquence observée 14 / 150 = 0,093 appartient à cet intervalle.
L'affirmation n'est pas remise en cause.
Partie C.
Une partie du stock de DVD de la ville est constituée de DVD de films
d’animation destinés au jeune public. On choisit un film d’animation au
hasard et on note X la variable aléatoire qui donne la durée, en
minutes, de ce film. X suit une loi normale d’espérance µ= 80 min et
d’écart-type s.
De plus, on estime que P(X > 92) = 0,10.
1. Déterminer le réel s et en donner une valeur approchée à 0,01.
On pose Z = (X-80) / s
Z suit la loi normale centrée réduite N(0 ; 1).
P(X < 92) = 1 - P(X> 92) = 0,9 ;
P(Z < (92-80) / s) = 0,9.
La calculatrice donne (92-80) / s= 1,28155 soit s = 12 / 1,28155 ~9,36.
2.
Un enfant regarde un film d’animation dont il ne connaît pas la durée.
Sachant qu’il en a déjà vu une heure et demie, quelle est la
probabilité que le film se termine dans les cinq minutes qui suivent ?
PX<90 (X < 95) = P ( 90 < X < 95) / P(X > 90).
P(X > 90)=1-P(X < 90)= 1-0,8573 =0,1427.
P(X < 95)=0,9455 ; P ( 90 < X < 95) =0,9455-0,8573 = 0,0882.
PX<90 (X < 95) =0,0882 / 1,427 ~0,62.
|
|
Exercice 3.
On considère la fonction f définie sur l’intervalle [0 ; +oo[ par f (x) = k e-kx où k est un nombre réel strictement positif.
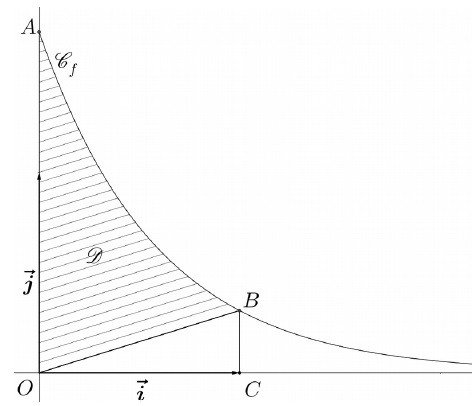
On appelle Cf sa représentation graphique dans le repère orthonormé.
On considère le point A de la courbe Cf d’abscisse 0 et le point B de la courbe Cf d’abscisse 1.
Le point C a pour coordonnées (1 ; 0).
1. Déterminer une primitive de la fonction f sur l’intervalle [0 ; +oo[.
F(x) = - e-kx.
En effet : F '(x) = - (-k) e-kx = k e-kx = f(x).
2. Exprimer, en fonction de k, l’aire du triangle OCB et celle du domaine D délimité par l’axe des ordonnées, la courbe Cf et le segment [OB].
Ordonnée du point B : f(1)=k e-k.
Aire du triangle OCB = OC * BC / 2 =1 * ke-k / 2 = 0,5 ke-k.
Aire du domaine D = F(1)-F(0) - 0,5 ke-k.
F(1) = -e-k ; F(0)= -1 ;
Aire du domaine D = -e-k +1 - 0,5 ke-k= 1 -e-k (1+0,5 k).
|
|
3.
Montrer qu’il existe une unique valeur du réel k strictement positive
telle que l’aire du domaine D vaut le double de celle du triangle OCB.
1 -e-k (1+0,5 k) =2 *0,5 ke-k.
1 = ke-k +e-k (1+0,5 k) = e-k (1+ 1,5k).
1-e-k -1,5 k e-k=0.
On pose g(x) = 1-e-x -1,5 x e-x.
g'(x) = e-x-1,5(e-x-x e-x) = e-x(-0,5 +1,5x).
La fonction e-x est strictement positive, g'(x) est du signe de 1,5 x-0,5.
Sur [0 ; +oo [, g'(x) = 0 pour x = 1 / 3.
g'(x) >0 pour x >1 /3 et négative pour x < 1 / 3.
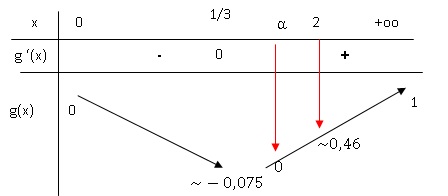
Sur [0 ; 1 / 3] la fonction g(x) est strictement décroissante et g(x) est négative.
L'équation 1-e-x -1,5 x e-x=0 n'a pas de solution sur cet intervalle.
Sur [ 2 ; +oo [ la fonction g(x) est strictement croissante et g(x) est positive.
L'équation 1-e-x -1,5 x e-x=0 n'a pas de solution sur cet intervalle.
La fonction g est continue et strictement croissante sur [1 / 3 ; 2 ].
La valeur zéro appartient à l'intervalle [( g(1/3) ; g(2)].
D'après le corollaire des valeurs intermédiaires, l'équation g(x) = 0 admmet une unique solution a sur [1 / 3 ; 2].
|
|