Mathématiques,
cube, tétraèdre, suite,
Bac S Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice 2.
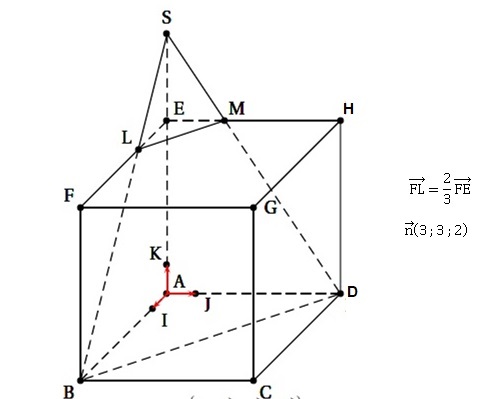
L’unité graphique représentant 1 mètre. Arète du cube = 6 m.
Les points L,M et S sont définis de la façon suivante :
• M est le point d’intersection du plan (BDL) et de la droite (EH) ;
• S est le point d’intersection des droites (BL) et (AK).
1. Démontrer, sans calcul de coordonnées, que les droites (LM) et (BD) sont parallèles.
Les plans (EFG) et (ABC) sont parallèles ( faces opposées du cube).
La droite (BD) est l'intersection des plans (ABC) et (BDL).
La droite (ML) est l'intersection des plans (EFG) et (BDL).
Le théorème de l'étagère conduit à : les droites (ML) et (BD) sont parallèles.
2. Démontrer que les coordonnées du point L sont (2 ; 0 ; 6).
F(6 ; 0 ; 6) : E(0 ; 0 ; 6) ; L(x ; y ; z).
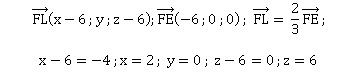
3. a. Donner une représentation paramétrique de la droite (BL).
B(6 ; 0 ; 0) ; L(2 ; 0 ; 6) ; vecteur directeur de cette droite :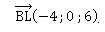
La droite passe par B, d'où x = -4t +6 : y = 0 ; z = 6t avec t réel.
b. Vérifier que les coordonnées du point S sont (0 ; 0 ; 9).
Représentation paramétrique de la droite (AK) : x = 0 ; y = 0 ; z = p avec p réel.
S est le point d’intersection des droites (BL) et (AK).
xS = -4t +6 = 0 d'où t = 1,5 ; yS =0 ; zS = p = 6 x1,5=9
4. a. Vérifier que le vecteur n, défini ci-dessous, est normal au plan (BDL).
B( 6 ; 0 ; 0) ; D ( 0; 6 ; 0) ; L( 2 ; 0. ; 6).
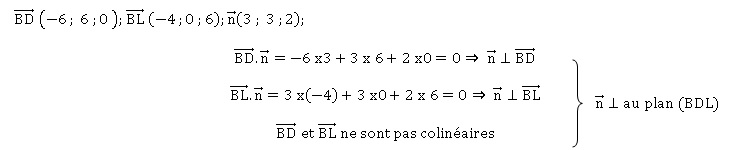
b. Démontrer qu’une équation cartésienne du plan (BDL) est : 3x +3y +2z −18 = 0.
3x +3y +2z + d = 0.
B(6 ; 0 ; 0) appartient à ce plan : 3 x6 +3 x0 +2 x0 +d=0, soit d = -18.
c. On admet que la droite (EH) a pour représentation paramétrique :
x = 0 ; y = s (s réel) ; z = 6.
Calculer les coordonnées du point M.
M appartient à la droite (EH) : xM = 0 ; yM = s ; zM = 6.
M appartient au plan (BDL) : 3 xM + 3yM + 2zM -18 = 0 soit 0 +3s+12-18 = 0 ; s = 2.
M( 0 ; 2 ; 6).
5. Calculer le volume du tétraèdre SELM. On rappelle que le volume V d’un tétraèdre est donné par la formule suivante :
V =1 / 3 ×Aire de la base × Hauteur.
S(0 ; 0 ; 9 ) ; E ( 0 ; 0 ; 6) ; hauteur SE = 3 m.
L(2 ; 0 ; 6) ; LE = [22 +02 +(6-6)2]½ = 2 m.
M(0 ; 2 ; 6) ; ME = [02 +(-2)2 +(6-6)2]½ = 2 m.
Aire de base ME x LE / 2 = 2 m2.
V = 1 / 3 x3 x2 = 2 m3.
6. L’artiste souhaite que la mesure de l’angle SLE soit comprise entre 55° et 60°.
Cette contrainte d’angle est-elle respectée ?
Dans le triangle SLE, la tangente de cet angle vaut : SE / EL = 3 / 2 = 1,5.
Cet angle mesure 56,3 °. La contrainte est respectée.
.
|
|
Exercice 4.
Le directeur d’une réserve marine a recensé 3 000 cétacés dans cette réserve au 1er
juin 2017. Il est inquiet car il sait que le classement de la zone en «
réserve marine » ne sera pas reconduit si le nombre de cétacés de cette
réserve devient inférieur à 2 000.
Une étude lui permet d’élaborer un modèle selon lequel, chaque année :
• entre le 1er juin et le 31 octobre, 80 cétacés arrivent dans la réserve marine ;
• entre le 1er novembre et le 31 mai, la réserve subit une baisse de 5% de son effectif par rapport à celui du 31 octobre qui précède.
On modélise l’évolution du nombre de cétacés par une suite (un). Selon ce modèle, pour tout entier naturel n, un désigne le nombre de cétacés au 1er juin de l’année 2017+n. On a donc u0 = 3000.
1. Justifier que u1 = 2926.
u1 = (u0 +80) x0,95 =2926.
2. Justifier que, pour tout entier naturel n, un+1 = 0,95un +76.
un+1 = 0,95( un +80) = 0,95un +76.
3. À l’aide d’un tableur, on a calculé les 8 premiers termes de la suite (un ). Le directeur a configuré le format des cellules pour que ne soient affichés que des nombres arrondis à l’unité.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
2
|
un
|
3000
|
2926
|
2856
|
2789
|
2725
|
2665
|
2608
|
2553
|
Quelle formule peut-on entrer dans la cellule C2 afin d’obtenir, par recopie vers la droite, les termes de la suite (un) ?
=0,95*B2+76
4. a. Démontrer que, pour tout entier naturel n, un >1520.
Initialisation : u0 > 1520, la propriété est vraie au rang zéro.
Hérédité : on suppose la propriété vraie au rang n : un >1520.
0,95 un > 0,95 x1520 ; 0,95 un >1444.
0,95 un +76 >1444 +76 ;
un+1 > 1444 +76.
un+1 > 1520.
Conclusion. la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel.
b. Démontrer que la suite (un) est décroissante.
un+1 -un = 0,95un +76 -un =76 -0,05 un.
un >1520 ; 0,05un >1520 x0,05 ; 0,05un >76.
un+1 -un < 0 ; un+1 < un ; la suite est décroissante.
c. Justifier que la suite (un) est convergente. On ne cherchera pas ici la valeur de la limite.
La suite est décroissante et minorée, elle est donc convergente.
|
|
5. On désigne par (vn) la suite définie par, pour tout entier naturel n, vn = un −1520.
a. Démontrer que la suite (vn) est une suite géométrique de raison 0,95 dont on précisera le premier terme.
vn+1 = un+1 −1520.
vn+1 =0,95un +76-1520.
vn+1 =un -0,05 un +76-1520.
vn+1 =un -1520 -0,05 un +76.
vn+1 =vn -0,05( un +1520).
vn+1 =vn -0,05 vn =0,95 vn.
Il s'agit donc d'une suite géométrique de raison égale à 0,95 et de premier terme :
v0 = u0-1520 = 3000-1520 = 1480.
b. En déduire que, pour tout entier naturel n, un = 1480×0,95n +1520.
vn = 1480 x 0,95n = un −1520.
un = 1480×0,95n +1520.
c. Déterminer la limite de la suite (un).
0 < 0,95 <1, donc 0,95 n tend vers zéro si n tend vers plus l'infini.
La limite de la suite (un) est égale à 1520.
6. Recopier et
compléter l’algorithme suivant pour déterminer l’année à partir de
laquelle le nombre de cétacés présents dans la réserve marine sera
inférieur à 2 000.
n←0
u←3000
Tant que u > 2000
n←n+1
u← 0,95 *u +0,76.
Fin de Tant que
La notation «←» correspond à une affectation de valeur, ainsi « n ←0 » signifie « Affecter à n la valeur 0 ».
7. La réserve marine fermera-t-elle un jour ? Si oui, déterminer l’année de la fermeture.
un = 1480×0,95n +1520 < 2000.
0,95n < (2000-1520) / 1480.
n ln(0,95) < ln [(2000-1520) / 1480].
n > ln [(2000-1520) / 1480] / ln(0,95).
n >21,95.
La réserve fermera l'année 2017 +22 soit en 2039.
|
|