Mathématiques,
cube, tétraèdre, nombres complexes,
Bac S Métropole 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
3.
On considère un cube.
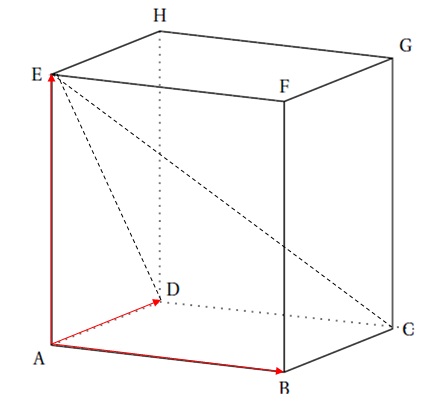
On admet que les droites (AG), (BH), (CE) et (DF), appelées grandes diagonales du cube, sont concourantes.
1. On considère le tétraèdre ABCE.
a. Préciser la hauteur issue de E et la hauteur issue de C dans ce tétraèdre.
(AE) est perpenduculaire au plan ABC : (AE) est la hauteur issue de E.
(BC) est perpenduculaire au plan ABE : (BC) est la hauteur issue de C.
b. Les quatre hauteurs de ce tétraèdre sont-elles concourantes ?
(AE) et (BC) ne sont pas coplanaires, donc non sécantes.
Les hauteurs du tétraèdre ne sont pas sécantes.
2. On considère le tétraèdre ACHF.
a. Vérifier qu'une équation cartésienne du plan ACH est x -y+z=0.
A(0 ; 0 ; 0) appartient à ce plan : xA -yA+zA=0.
C(1 ; 1 ; 0) appartient à ce plan : xC -yC+zC=1-1+0=0.
H(0 ; 1 ; 1) appartient à ce plan : xH -yH+zH=0-1+1=0.
b. En déduire que (FD) est la hauteur issue de F de ce tétraèdre.
F(1 ; 0 ; 1) et D(0 ; 1 ; 0).
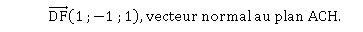
(FD) est la hauteur issue de F du tétraèdre ACHF.
c. Préciser les hauteurs du tétraèdre ACHF issues respectivement des sommets A, C et H. les 4 hauteurs sont-elles concourantes ?
(AG) est la hauteur issue de A, (CE) et la hauteur issue de C et (HB) est la hauteur issue de H.
Les 4 hauteurs correspondent aux grandes diagonales du cube, elles sont donc concourantes.
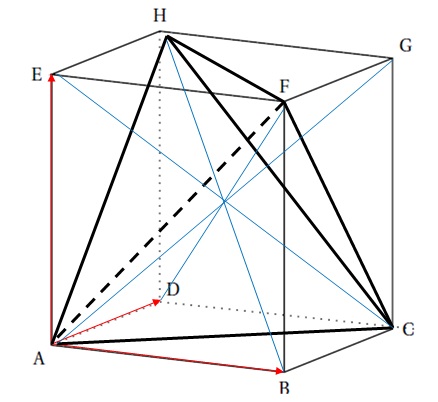
Un tétraèdre dont les 4 hauteurs sont concourantes est appelé orthocentrique.
|
|
Partie B.
On
considère le tétraèdre MNPQ dont les hauteurs issues des sommets M et N
sont sécantes en un point K. les droites (MK) et (NK) sont donc
orthogonales aux plans (NPQ) et(MPQ) respectivement.
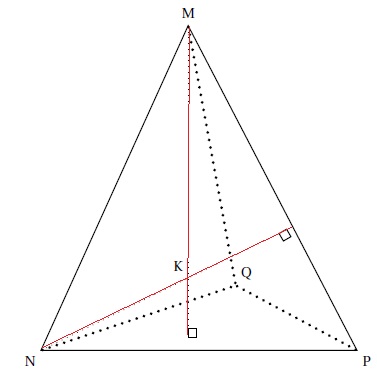
1.a
Justifier que la droite (PQ) est orthogonale à la droite (MK). On
admet de même que les droites (PQ) et (NK) sont orthogonales.
(MK) est orthogonale au plan ( NPQ). D'après le théorème de la porte,
(MK) est orthogonale à toute droite de ce plan et en particulier
à (PQ).
1.b. Que peut-on en déduire relativemennt à la droite (PQ) et au plan (MNK) ? Justifier.
(PQ) est orthogonal à (NK) et à (MK) ; (PQ) et (MK) sont deux droites
sécantes du plan ( MNK). Donc (PQ) est orthogonale au plan ( MNK).
2. Montrer que les arètes [MN] et (PQ] sont orthogonales.
(PQ) étant orthogonale au plan (MNK), (PQ) est donc orthogonale à toute droite de ce plan. (PQ) est orthogonale à (MN).
Si un tétraèdre est orthocentrique, alors les arètes opposées ( elles n'ont pas de sommet commun) sont orthogonales deux à deux.
Partie C.
On considère les points R(-3 ; 5 ; 2) ; S(1 ; 4 ; -2) ; T(4 ; -1 ; 5) et U(4 ; 7 ; 3).
1. Le tétraèdre RSTU est-il orthocentrique ? Justifier.
 . .
Les deux arètes opposées RU et ST ne sont pas orthogonales : le tétraèdre RSTU n'est pas orthocentrique.
|
|
Exercice 4.
On pose z0 = 8 et pour tout entier naturel n : zn+1 = (3 -i3½) / 4 zn.
On note An le point du plan d'affixe zn.
1.a. Vérifier que : z= (3 -i3½) / 4 = 3½ / 2 exp(-ip/6).
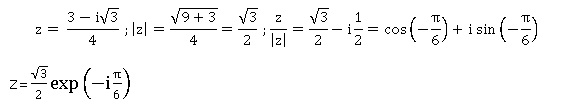
b. En déduire l'écriture des bombres complexes z1, z2 et z3 sous forme exponentielle et vérifier que z3 est un imaginaire pur dont on précisera la partie imaginaire.
z1 =4 x 3½ exp(-ip/6).
z2 = 3½ / 2 exp(-ip/6).z1=6 exp(-ip/3)
z3 = 3½ / 2 exp(-ip/6).z2=3 x 3½ exp(-ip/2).
c. Représenter graphiquement les points A0, A1, A2 et A3.

2.a. Démontrer par récurrence que, pour tout entier naturel n , zn = 8 (3½/2)n exp(-inp/6).
Initialisation : la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n.
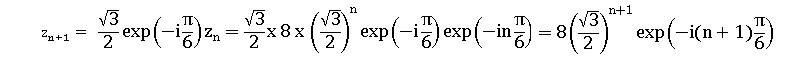
Conclusion : la prorpiété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel.
2.b. On pose un = |zn|. Déterminer la nature et la limite de cette suite.
|zn| = 8 (3½ / 2)n = z0 (3½ / 2)n ; suite géométrique de premier terme 8 et de raison 3½ / 2.
0 < 3½ / 2 < 1, donc (3½ / 2)n tend vers zéro quand n tend vers plus l'infini.
un tend vers zéro quand n tend vers plus l'infini.
3.a. Démontrer que pour tout entier naturel k : (zk+1-zk) / zk+1 = -i / 3½.
En déduire que AkAk+1=OAk+1 / 3½.
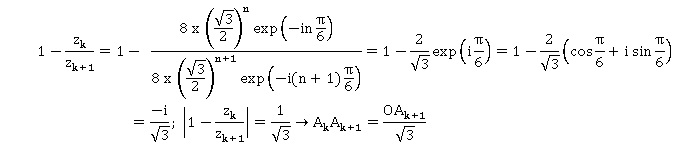
b. Pour tout entier naturel n , on appelle ln la longueur de la ligne brisée reliant dans cet ordre les points A0, A1, A2, ...An. Démontrer que la suite (ln) est convergente et calculer sa limite.
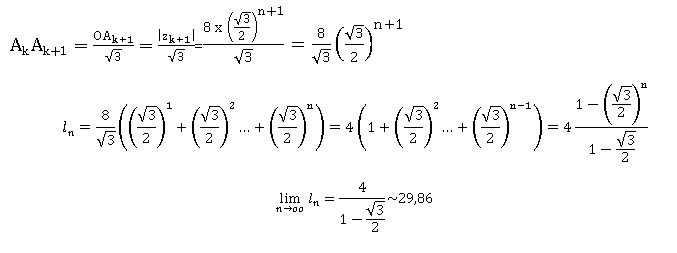
|
|