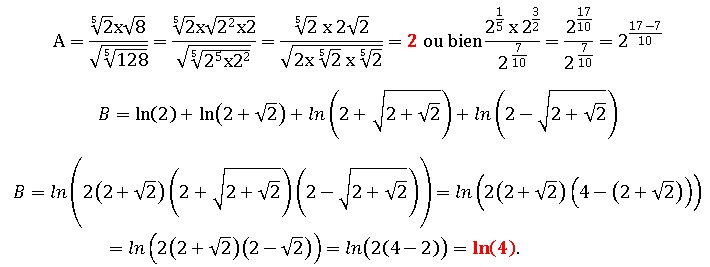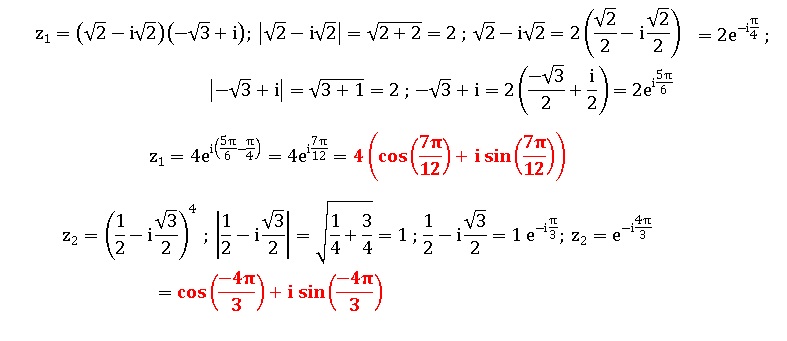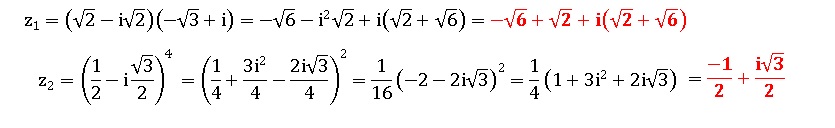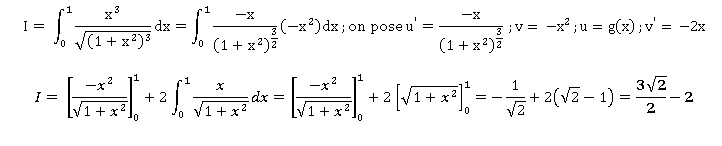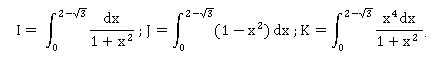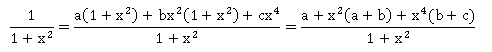Mathématiques,
consours EMIA 2015.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 1 point.
Ecrire plus simplement les expressions suivantes.
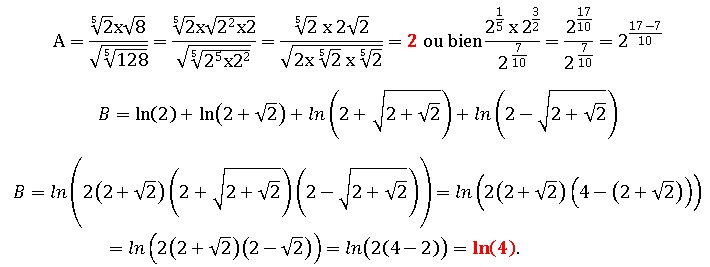
Exercice 2. 1 point.
Ecrire sous forme algébrique et trigonométrique les nombres complexes suivants :
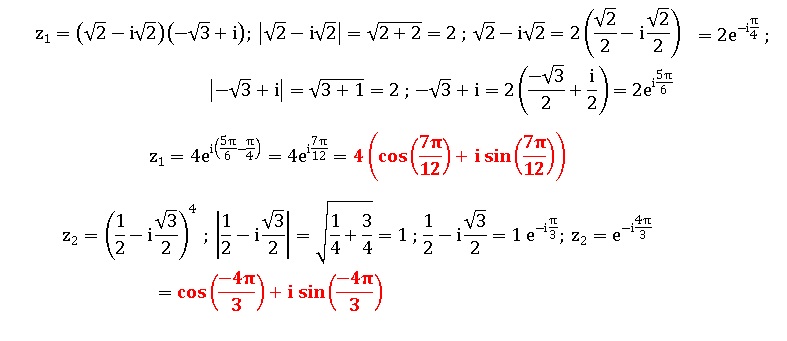
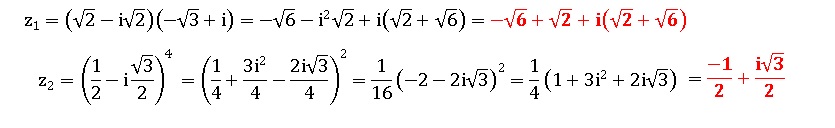
Exercice 3. 1,5 points.
Résoudre dans R les inéquations :
ln(2-x) + ln(x+4) > ln(3x+2).
2-x doit être positif soit x < 2.
x+4 doit être positif soit x > -4.
3x+2 doit être positif soit x >-2 / 3.
Donc x doit être dans l'intervalle ]-2 /3 ; 2 [.
(2-x)(x+4) > 3x+2.
-x2 -4x+2x+8 > 3x+2.
x2+5x-6 < 0.
Les solutions de x2+5x-6 = 0 sont : 1 et -6.
Les solutions de x2+5x-6 < 0 sont : 1 et 6]-6 ; 1[.
Par suite les solution de cette inéquation sont ]-2 / 3 ; 1 [.

Exercice 4. 1 point.
Résoudre dans R x R le système : x+y = 25 et ln x + ln y =2 ln 12.
x et y doivent être positifs.
ln(xy) = ln(122) ; xy = 144.
x = 25-y ; (25-y) y = 144.
y2-25y + 144 = 0. D = 252 -4 x144=49 ; solutions : (25±7) / 2 =soit 16 et 9.
|
...
|
|
Exercice 5. 1,5 points.
Soient (xn) et (yn) les suites définies par x0 = 3 et y0 = 1 avec n entietr naturel.
xn+1=1,2 xn +0,4yn +1 ; yn+1=0,4 xn +1,8yn+2.
1. Démontrer par récurrence que les points Mn de coordonnées (xn, yn) sont sur la droite d'équation 2x-y=5.
Initialisation : M0(3 ; 1) est sur la droite car ses coordonnées vérifient 2x-y = 5
Hérédité : la propriété est supposée vraie au rang n. 2xn-yn = 5.
2xn+1 - yn+1=2 xn - yn +1=5
Conclusion : la propriété est vraie au rang zéro et héréditaire; elle est vraie pour tout n entier.
2. En déduire xn+1 en fonction de xn.
xn+1=0,5 yn+1 +2,5 = 0,2 xn +0,9 yn +3,5.
9/4xn+1=1,2 *9/4xn +0,4*9/4yn +9/4.
Soustraire : 5/4xn+1 =2,5 xn -5/4.
xn+1 = 2 xn -1 et yn+1 = 2xn+1-5 = 4 xn -6.
3. Démontrer que xn est un multiple de 5 si et seulement si yn est un multiple de 5.
yn = 5 k avec k entier.
xn =2,5 + 0,5yn = 2,5+2,5 k = 2,5(k+1)=5(k+1)/2.
Si xn = 5 k avec k entier alors yn =2xn -5= 10k-5 =5(2k+1).
4. Démontrer que xn = 2n+1 +1.
Initialisation : x0 = 3 = 20+1 +1 est vraie
Hérédité : la propriété est supposée vraie au rang n. xn = 2n+1 +1.
xn+1 = 2 xn -1=2 x2n+1 +2-1 =2n+2 +1.
Conclusion : la propriété est vraie au rang zéro et héréditaire; elle est vraie pour tout n entier.
Exercice 6. 1,5 points.
Soit f la fonction définie sur R par f(x) = E(x) +(x-E(x))2 où E(x) désigne la fonction partie entière.
1. Démontrer que quel que soit x réel, f(x+1) = f(x) +1. En donner une interprétation graphique.
f(x+1) = E(x+1) +(x+1-E(x+1))2 .
E(x) = p avec p entier; donc p < x < p+1.
p+1 < x+1 < p +1 +1 ; donc E(x)+1 = p+1 = E(x)+1.
f(x+1) = E(x)+1 +(x+1-E(x)-1))2 .
f(x+1) = E(x)+1 +(x+-E(x))2 = f(x) +1.
Quand x augmente de 1, son image augmente de 1. Sur [1 ; 2[ la courbe
se déduit de la courbe obtenue sur [0 ; 1[ par translation de vecteur de coordonnées (1 ; 1)..
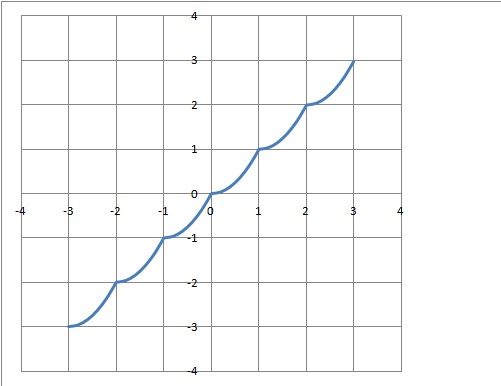
2. Etudier f(x) et tracer succinctement sa courbe représentative sur [-3 ; +3 ].
Sur [-3 ; -2 [ : f(x) = -3 + (x+3)2 ; sa dérivée est f '(x) = 2(x+3) positive.
f(x) est croissante sur cet intervalle.
Exercice 7. 1,5 points.
On considère trois événements A, B, C d'un univers des possible W. On donne P(A n B), P(A), P(B) et P A n B(C).
Parmi les probabilités suivantes quelles sont celles que l'on peut calculer et comment ?
P(A u B), PB(A), PB(non A), Pnon B(A), PA(B), P(A n B n C), P(non A n non B), P(non A u non B).
P(A u B) = P(A) + P(B) -P(A n B).
PB(A) = P(A n B) / P(B).
PA(B) = P(A n B) / P(A).
P(non A )= 1 -P(A) ; P(non B )= 1 -P(B) ; P(non A n non B)= P(non A) + P(non B) -P(non A u non B) |
....
|
Exercice 8. 2 points.
Combien
de fois faut-il jeter un dé non pipé pour que la probabilité d'obtenir
au moins un 6 soit supérieure à 50 % ? à 67 % ? On utilisera une
variable aléatoire égale au nombre de 6 obtenus sur n lancers d'un dé
non pipé, dont on précisera la loi et les paramètres, et l'on donnera
une valeur approchée de la quantité cherchée en utilisant les
approximations : ln 2 ~0,7 ; ln 3 ~1,10 ; ln 5 ~1,61.
Après un lancer, la probabilité d'obtenir 6 est 1 / 6 et celle d'obtenir 1, 2, 3, 4 ou 5 est égale à 5 / 6.
Après 2 lancers, la probabilité d'obtenir au moins un 6 est : 1-(5 / 6)2.
Probabilité d'obtenir au moins 6 sur n lancers = 1 - probabilité d'obtenir 1, 2, 3, 4 , 5. sur n lancers = 1 -(5 /6)n.
0,50 = 1 -(5/6)n ; ln 0,5 = n ln(5 / 6) = n(ln 5 -ln 6) =n( ln 5 -ln 2 -ln 3).
n = -ln(2) / (ln 5 -ln2 -ln 3) ~ -0,7 /(1,61 -0,7 -1,10) ~3,68 soit 4 lancers.
0,67 = 2 /3 = 1 -(5/6)n ; -ln 3 = n ln(5 / 6) = n(ln 5 -ln 6) =n( ln 5 -ln 2 -ln 3).
n =--ln 3 / (ln 5 -ln2 -ln 3) ~-1,10 /(1,61 -0,7 -1,10) ~5,79 soit 6 lancers.
Exercice 9. 1,5 point.
Soient f(x) et g(x) les fonctions définies sur R. Calculer meurs dérivées et calculer en intégrant par parties l'intégrale I.
f(x) = (1+x2)½ ; on pose u = 1 +x2 ; u' = 2x ; f = u½ ; f ' = ½u-½u' = x / (1+x2)½ .
g(x) = 1 / (1+x2)½ ; g = u-½ ; g ' = -½u-3 /2u' = -x / (1+x2)3 / 2 .
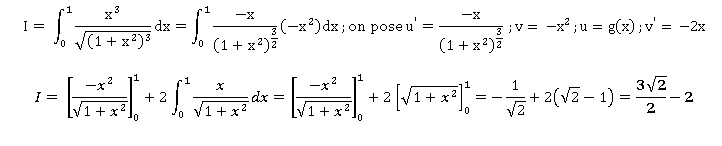
Exercice 10. 1,5 points.
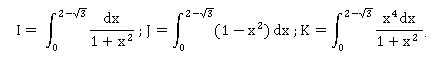
1. Calculer (2 -3½)3, (2-3½)4 et l'intégrale J.
(2-3½)2 = 4+3-4 *3½=7-4 *3½.
(2-3½)3 =(2-3½)(7-4 *3½)=14+12-15*3½ = 26-15*3½.
(2-3½)4 =(7-4 *3½)2=49 +48-56*3½ = 97-56*3½.
Primitive de 1 -x2 : x-x3 / 3 ; J = 2-3½ -(2-3½ )3 =2-3½ -26+15*3½= -24+14*3½.
2. Calculer les coefficients a, b, c tels que 1 / (1+x2) = a + bx2 +cx4 /(1+x2).
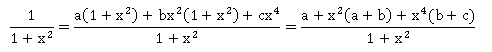
On identifie : a = 1 ; a+b = 0 soit b = -1 ; b+c = 0 soit c = 1.
3. Démontrer que pour tout réel positif x : x4 /(1+x2) < x3/2, et en déduire une majoration de K.
(x-1)2 > 0 ; pour x > 0 : x3(x-1)2 > 0 ; x5 -2x4 +x3 > 0 ;
x5 +x3 > 2x4 ; x3(1+x2) > 2x4 ; x3/2 > x4 /(1+x2)
K est majorée par une primitive de x3 / 2 , soit x4/8 sur [0 ; 2-3½]
K est majorée par (2-3½)4 .
4. Déduire des questions précédentes un encadrement de I.
1-x2 =1 / (1+x2) -x4 /(1+x2)..
I = J -K.
I est minorée par J-(2-3½)4 .
|
. Exercice 11. 3 points.
Déterminer ce qu'effectue et renvoie l'algorithme suivant.
Variables : n, i, s : entiers.
Début
Ecrire ( " taper un entier naturel strictement positif " )
Lire n
Si n=1 alors écrire 1 sinon
s <-- 1
i <-- n
Tant que i >1 faire
s <--s +i * i
i <-- i-1
Fin Tant que
Ecrire s
Fin si.
n
|
1
|
2
|
3
|
4
|
s
|
|
1
|
1
|
1
|
i
|
|
2
|
3
|
4
|
i > 1
|
|
vrai
|
vrai
|
vrai
|
s
|
|
1+2 x2=5
|
1+3 x3=10
|
1+4 x4=17
|
i
|
|
2-1=1
|
3-1=2
|
3
|
i > 1
|
|
faux
|
vrai
|
vrai
|
s
|
|
|
10+2x2=14
|
17+3x3=26
|
i
|
|
|
1
|
2
|
i >1
|
|
|
faux
|
vrai
|
s
|
|
|
|
26+2x2=30
|
i
|
|
|
|
1
|
i >1
|
|
|
|
faux
|
on écrit s
|
1
|
5 = 12 +22
|
14= 12 +22 +32.
|
30= 12 +22 +32+42. |
Cet algorithme calcule la somme des carrés des n premiers entiers non nuls.
Exercice 12. 3 points.
On considère l'équation x2-2y2 = 1 d'inconnues x
et y appartenant à N*. Ecrire l'algorithme permettant de déterminer
toutes les solutions de cette équation pour lesquelles y < 100.
y= racine carrée ((x2-1)/2) et y est un entier < 100
Variable x, y entier, z réel.
x<--2 ; z = racine carrée ((x2-1)/2)
Tant que z < 100 faire
z= racine carrée ( (x+1)*(x-1)/2)
Si z entier non nul alors y <--z ; écrire x, y.
x < x+1.
Fin Tant que.
x
|
2
|
3
|
4
|
...
|
17
|
...
|
99
|
z
|
1,5½
|
2
|
7,5½
|
|
12
|
|
70
|
z < 100
|
vrai
|
vrai
|
vrai
|
|
vrai
|
|
vrai
|
y
|
|
2
|
|
|
12
|
|
70
|
z entier
|
faux
|
vrai
|
faux
|
|
vrai
|
|
vrai
|
écriture
|
|
3 ; 2
|
|
|
17 ; 12
|
|
99 ; 70
|
.
|
|