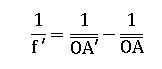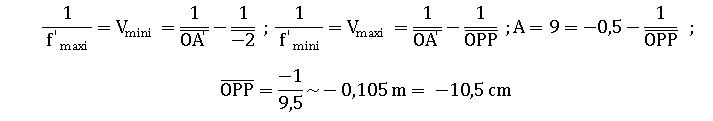QCM
Physique, concours CPR 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Mécanique. Détermination e la charge
massique d'un électron.
7
points.
Un
faisceau d'électron produit par un canon à électrons arrivant en O avec
la vitesse V0 est alors soumis, au cours de son mouvement le
long de la
distance d, à l'action d'un champ électrostatique E uniforme créé par
deux plaques P et P' orthogonales au plan ( xOy) et distantes de l. Le poids de l'électron
est négligeable.
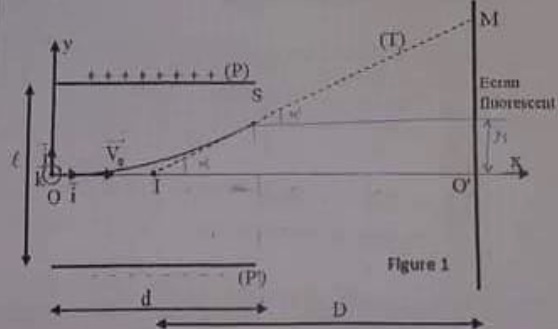
On désigne
par U = VP-VP'
la différence de potentielle entre (P) et (P') et par D la distance du
pint I à l'écran fluorescent. On prend l'instant t=0 l'instant où
l'électron passe en O.
19. L'équation de
la trajectoire d'un électron dans le repère proposé s'écrit :
A. y = eU / (l mV02)
x2.
B. y = eU / (2l mV02)
x2 . Vrai.
C. y = eU / (2l mV02)
x2 + 0,5 l.
D.
y = eU /
(l mV02)
x2 + 0,5 l.
Coordonnées du vecteur accélération : ( 0
; e U / (m l ) ).
Coordonnées du vecteur
vitesse : ( V0 ; e U t / (m l
)).
Coordonnées du vecteur position : (x= V0 t ; y= e U t2 / (2m l )).
Trajectoire : y
= eU / (2l mV02)
x2 .
20.
Le
faisceau sort du champ électrostatique en un point S et poursuit son
mouvement et heurte un écran fluorescent en un point M. La droite (T)
représente la tangente à la trajectoire au point S. L'expression de la
déviation électrique O'M d'un électron s'écrit :
A. eDU /(l m V02).
B. edDU /(m V02).
C. edDU /(l m V0).
D. edDU /(l m V02).
Vrai.
Ordonnée du point S :
yS
= eU / (2l mV02)
d2 .
Tan a = O'M / D= yS
/ (0,5d) , O'M = yS D /(0,5 d) = edDU /(
l m V02).
Le
faisceau d'électrons arrivant en O est soumis en plus du champ
électrostatique précédent à un champ magnétique uniforme B dirigé vers
l'arrière de la figure et orthogonal à E. B = 1,01 mT et le faisceau
heurte l'écran en O'.
O'M = 5,4 cm ; D = 30 cm ; U = 1200 V ; l = 2 cm ; d = 6 cm.
21. L'expression de la vitesse V
des électrons en fonction de E et B est :
A. (E / B)2.
B. B / E.
C. E / B. Vrai.
C. EB.
La force électrique et la
force magnétique se compensent : eE = e v B ; v = E / B.
22. Le rapport e / m vaut ( en C kg-1)
:
A. 1,76 1011.
Vrai.
B. 2 1017.
C. 2,3 1011.
D. 2,76 1011.
edDU /(l m V02)=
5,4 10-2 avec V0 = 1200 /(0,02 x1,01 10-3)
=5,94 107 m /s.
e / m = 5,4 10-2 l V02/
(d D U) = 5,4 10-2 x0,02 x(5,94
107)2 / (0,06 x0,30 x1200) =1,76 1011.
|
...
|
|
Pendule de torsion.
Un pendule de torsion est constitué par un fil de torsion de constante
de torsion C, auquel est accroché un fléau. Le fléau est constitué
d'une tige AB de longueur 2 L, aux extrémités de laquelle sont
disposées deux sphères en platine pleines, homogènes, de masse m, de
rayon r, centrées respectivement en A et en B. La masse de la tige sera
supposée négligeable devant celle des sphères. Les frottements seront
négligés.
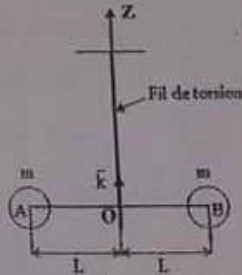
On fait tourner, horizontalement, dans le sens positif, le fléau d'un
angle q0
= p /3. On repère
la position du fléau par l'abscisse angulaire q
et on choisit comme origine du temps l'instant du lâcher du fléau. On
prend comme état de référence de l'énergie potentielle de pesanteur le
plan horizontal contenant le fléau et on considère l'énergie
potentielle de torsion nulle pour q = 0.
23.
L'énergie mécanique du système { fléau + fil de torsion } a pour
expression :
A. Em =mL2q'2
+0,5 Cq2. Vrai.
B. Em =2mL2q'2
+0,5 Cq2.
C. Em =mL2q'2
+ Cq2.
D. Em =mLq'2
+0,5 Cq2.
Moment d'inertie des deux boules par rapport à O : 2mL2 ( si r << L). La masse de la barre étant négligeable, le moment d'inertie .du système vaut J = 2mL2.
Energie cinétique : ½Jq'2 =mL2q'2. Energie potentielle : ½Cq2.
24. L'équation différentielle du mouvement du fléau s'écrit :
A. 2mL2q" +Cq = 0. Vrai.
B. 4mL2q" +Cq = 0.
C. mL2q" +Cq = 0.
D. mLq" +Cq = 0.
Couple de rappel exercé par le fil : - Cq.
Le théorème du moment cinétique donne, en absence de frottement : J q" = - Cq avec J = 2mL2.
25.. Le fléau a un mouvement oscillatoire périodique de période T0 = 296 s. L'équation horaire q(t) du mouvement du fléau s'écrit :
A. q(t) = p / 3 sin ( 0,02 t).
B. q(t) = p / 3 cos ( 0,02 t). Vrai.
C. q(t) = p / 3 sin ( 0,02 t-p/2).
D. q(t) = p / 3 cos ( 0,02 t + p/2).
w = 2p / T0 = 6,28 / 296 ~0,02 rad / s.
q(t) = A cos( wt + B) ; q(0 ) = p / 3, d'où A = p /3 et B = 0.
Electricité, électromagnétisme.
A. Modèle de Thomson de l'atome d'hydrogène.
Celui-ci
est constitué d'un électron supposé ponctuel, de charge négative -e et
d'une charge positive+e représentant le proton répartie uniformément en
volume dans une sphère de centre O et de rayon a0.
26. Le champ électrostatique créé par le proton seul en tout point M de l'espace ( OM= r) est donné par l'expresion.
A. E(r) = e /(4pe0a03) r2 si r < a0 et E(r) = e / (4pe0r) si r > a0.
B. E(r) = e /(4pe0a03) r si r < a0 et E(r) = e / (4pe0r2) si r > a0. Vrai.
C. E(r) = e /(4pe0r2) r2 si r < a0 et E(r) = e / (4pe0a03)r si r > a0.
D. E(r) = e /(4pe0r) si r < a0 et E(r) = e / (4pe0a02)r2 si r > a0.
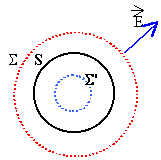 La sphère S de
rayon R porte la charge volumique uniforme
r. Par raison de symétrie le champ est
radial La sphère S de
rayon R porte la charge volumique uniforme
r. Par raison de symétrie le champ est
radial
Flux envoyé
à travers la sphère
S
de rayon r : F=
4pr2E.
charge
intérieure à S=
charge de S =4/3
pa03r= e.
Théorème de Gauss :
4pr2E = e / e0 ; E = e / (
4pe0 r2.)
Flux envoyé
à travers la sphère
S
' de rayon r : F=
4pr2E.
charge
intérieure à S '=
charge de S =4/3
pr3r= Q = e(r/a0)3.
Théorème de Gauss :
4pr2E = Q / e0 ; E = e r/ (
4pe0 a03)
27. L'expression du potentiel V de ce champ électrique en prenant une référence de potentiel à l'infini est :
E = -dV/dr ; V (r)= e / (4pe0r) si r > a0.
V (r)= - e /(4pe0a03) 0,5r2+ Cste si r < a0.
Continuité du potentiel à la surface de la sphère : - e /(4pe0a03) 0,5a02+ Cste = e / (4pe0a0).
Cste = 3 e /(8pe0a0) ; V(r) =e /(8pe0a03) (3a02-r2). Réponse C.
|
....
|
Oscillations libres dans un circuit RLC série.
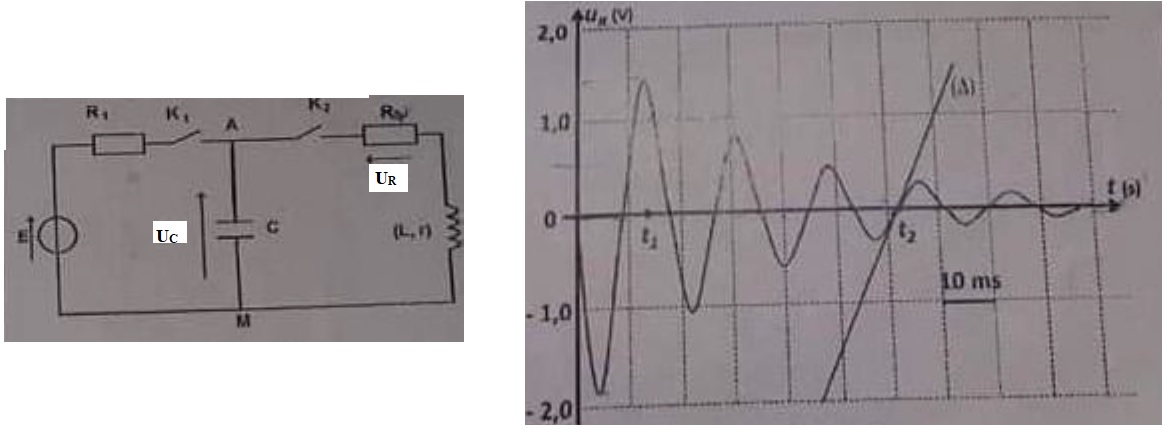
Le condensateur est initialement non chargé. On ferme K1 ; une fois le régime permanent atteint on ouvre K1 et on ferme K2 à un instant choisi comme origine des dates.
R = 50 ohms ; L = 0,8 H ; r = 42,86 ohms ; on pose l = (R+r) / (2L) et on note T0 la période propre de l'oscillateur.
28. L'équation différentielle vérifiée par la tension uR(t) peut s'écrire :
Ri + UC+ Ldi/dt + r i = 0 avec Uc =Q / C ; i = dQ /dt=C dUc /dt ; i = UR / R.
dUR dt +dUc/dt +Ld2i/dt2 +rdi /dt = 0
dUR dt +UR / (RC) +L/ R d2UR/dt2 +r/ R dUR /dt = 0.
(R + r)dUR/dt +UR / C+ Ld2UR/dt2 = 0.
(R + r) / L dUR/dt +UR / (LC)+ d2UR/dt2 = 0.
2 l dUR/dt +UR / (LC)+ d2UR/dt2 = 0.
De plus LC = T02 / (4p2).
d2UR/dt2 + 2 l dUR/dt +4p2 / T02 UR =0. Réponse B.
29. La pseudo-période et la prériode propre T0 sont liés par 1 / T02 -1/T2 = l2 / (4p2).
La valeur de C est : ( en µF) 9,7 ; 12,7 ; 13,2 ; 15,5.
l = 92,86 / 1,6 = 58,075 ; l2 / (4p2) =85,32.
D'après le graphe 5 T = 88 ms ; T = 17,6 ms = 0,0176 s.
1 / T02=1/0,01762+85,32 = 3313,6 ; T0 = 0,01737 s.
De plus T0 = 2p ( LC)½ ; C = 0,017372 / (4 x3,142 x0,8 )=9,5510-6 F ~ 9,6 µF. Réponse A.
30. On note E(t) l'énergie du circuit à l'instant t. Les expressions de cette énergie aux instants t1 et t2 indiqués sur la figure sont :
A la date t1, UR est maximale, donc l'intensité
est maximale : di/dt = 0. La bobine stocke toute l'énergie du circuit ;
la tension aux bornes de la bobine est égale à ri.
E(t1) = ½Li2 avec i=UR / R. E(t1)=0,5 L UR2 / R2.
A la date t2, l'intensité est nulle ; le condensateur stocke l'énergie du circuit : E(t2) = 0,5 C Uc2 avec Uc =- L di/dt = -L / R dUR/dt.
E(t2)=0,5 C L2 / R2 (dUR /dt)2. Réponse D.
31. La droite (D) représente la tangente à la courbe à l'instant t2. La valeur de l'énergie dissipée pat effet Joule dans le circuit entre t1 et t2 est ( en mJ) :
3,5 ; 2,2 ; 1,5 ; 0,35.
Coefficient directeur de cette droite : 2,5 / 0,020 =125; di/dt =125 / 50=2,5 ; Uc = -Ldi/dt = -0,8 x2,5 = -2 V.
Energie stockée dans le condensateur ( donc dans le circuit) à t2 : 0,5 x 9,7 10-6 x(-2)2 = 1,94 10-5 J
Energie stockée dans la bobine ( donc dans le circuit) à la date t1 : 0,5 L i2 = 0,5 x0,8 x(1,5 / 50)2 = 3,6 10-4 J.
Energie perdue par effet Joule entre ces deux instants : 3,6 10-4 -1,94 10-5 =3,4 10-4 J~0,34 mJ.
|
|
Optique.
L'oeil
peut être modélisé par une lentille convergente de distance focale
variable. Au repos la distance focale de l'oeil est maximale : l'oeil
voit un objet AB placé au ponctum remotum, défini comme le point le
plus éloigné dont l'oeil peut former une image A'B' nette sur la
rétine. En accommodation maximale, la distance focale de l'oeil est
minimale : l'oeil voit un objet situé à son punctum proximum. Pour un
oeil normal le punctum remotum est à l'infini et le punctum proximum à
d = 25 cm. On suppose que le centre O de la lentille est confondu avec
le sommet S de l'oeil.
32. La formule de conjugaison de Descartes s'écrit :
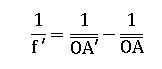 Réponse B. Réponse B.
On rappelle que l'amplitude d'accommodation est définie par la différence A = Vmax -Vmin où Vmax et Vmin sont respectivement la vergence maximale et la vergence minimale de l'oeil.
33. L'amplitude d'accommodation d'un oeil normal est ( en dioptries) : 3 ; 4 ; 5 ; 6.
Objet à l'infini : 1/ f ' maxi =Vmini = 1 / OA'.
Objet au punctum proximum : 1 / f ' mini = Vmaxii =1/OA'- 1 / (-0,25)
A = 1 / 0,25 = 4 dioptries.
L'oeil d'une personne ne voit pas distinctement les objets situés à une
distance supérieure à 2 m. Il possède une amplitude d'accommodation de
9 dioptries.
34. La position de son punctum proximum PP par rapport à S a pour valeur algébrique ( en cm) : -9 ; -10,5 ; -11 ; -12.
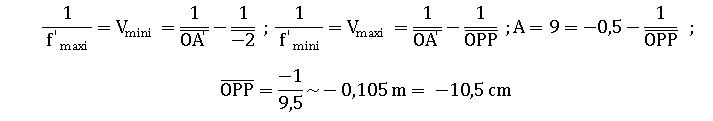 Réponse B. Réponse B.
35. Pour cet oeil, la personne est : myope, hypermétrope.
La vision de loin est floue.
36. Pour permettre à cette personne un vision à l'infini, il faut corriger son ponctum remotum PR avec une lentille :
divergente ; convergente.
Des lentilles divergentes permettent de corriger la myopie.
37. On suppose que
le centre O de la lentille correctrice est confondu avec le sommet S de
l'oeil. La distance focale de cette lentille est : -25 cm ; -2 m ; 2 m
; 2 cm.
Soit V la vergence de la lentille correctrice :
Pour un objet à l'infini et l'oeil corrigé : V + Vmin =1 / OA'
Pour un objet situé à 2 m et l'oeil non corrigé : Vmin = 1 /OA-+1 / 2.
Soustraire : V = -1 / 2. Distance focale de cette lentille : - 2 m.
Thermodynamique.
Une mole de gaz parfait subit la transformation cyclique suivante :
une compression isotherme à la température T de A(P1, V1, T) à B(P2, V2, T).
Un échauffement à volume constant V2 de B(P2, V2, T) à C(P3, V2, T ').
Une détente adiabatique réversible de C à A.
On pose a = V1 / V2 et g = Cp / Cv.
38. Le cycle décrit par le gaz dans un diagramme (P, V) est :
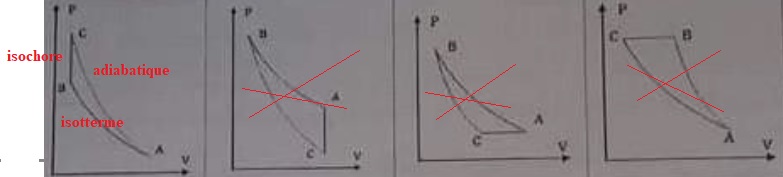
Réponse A.
39. Les expressions de P2, P3, T ' en fonction de P1, a, T et g sont :
Isotherme AB : P1V1 = P2V2 ; P2 =P1 V1 / V2 = P1a.
Adiabatique CA : P3 V2g = P1V1g ; P3 = P1 ag.
On pose ß = 1/g -1 ; T ' P3ß = T P1ß ; T ' = T ( P1 / P3 )ß= T ag-1.
Echauffement isochore BC : P2V2 =P1 V1= RT ; P3 V2 = R T '.
Réponse B.
40. Les expressions du travail WAB reçu par le système dans la transformation AB et du transfert thermique QAB correspondant sont :
Travail élémentaire d W = -PdV avec P = RT / V ; dW = -RT dV / V = -RT d ln(V).
Intégrer de 1 à 2 : WAB = -RT ln(V2 / V1 ) = RT ln (a).
L'énergie interne du gaz parfait ne varie pas ( T = constante) : QAB + WAB = 0 ; QAB = -RT ln(a). Réponse C.
|
|


 La sphère S de
rayon R porte la charge volumique uniforme
r. Par raison de symétrie le champ est
radial
La sphère S de
rayon R porte la charge volumique uniforme
r. Par raison de symétrie le champ est
radial