Physique,
objectif Mars.
Concours général 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Quittons
notre berçeau !
L'équation
fondamentale de l'astronautique ( équation de Tsiolkovski )
reliant la vitesse instantanée de la fusée v(t) à sa masse m(t) à
l'instant t est :.
Dv =
v(t) -v0 = ve ln( m0 / m(t)).
m0 : masse initiale de la fusée ; v0 : vitesse
initiale de la fusée ; ve : vitesse d'éjection des gaz par
rapport au référentiel de la fusée, supposée constante.
Dans cette équation, la fusée n'est soumise qu'à la force de poussée
fournie par son moteur. Elle ne tient compte d'aucune autre action
extérieure.
Objectif
Mars.
Le lanceur est constitué de 2 propulseurs d'appoint ( les
boosters), de deux étages cryogéniques et d'un module d'exploration. Le
lanceur sera lancé depuis la surface de la terre et aura pour objectif
de mettre un module d'exploration en orbite autour de Mars.
I. D'où décoller depuis la
terre ?
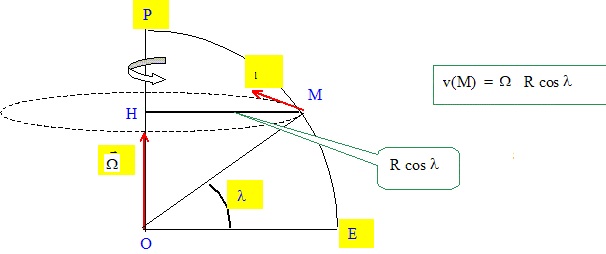
Considérons le cas particulier d'un point M décrivant, dans un
référentiel donné, une trajectoire circulaire et uniforme. Durant le
mouvement, le rayon du cercle CM balaie un angle q pendant la durée Dt, C étant le centre du
cercle. La vitesse angulaire de M dans ce référentiel est w = q / Dt.
On s'intéresse au lanceur juste avant le décollage dans le référentiel
géocentrique, référentiel dont l'origine est le centre de la terre et
dont les trois axes pointent vers des étoiles lointaines qui paraissent
fixes.
On assimile le lanceur à un point matériel M fixe à la surface de la
terre de centre O.
1. Quelle est la
valeur de la vitesse angulaire W
du lanceur dans le référentiel géocentrique ?
Jour sidéral TT = 23 h 56 min 4 s = 86164 s.
La terre accomplit un tour sur elle même en 86164 s.
W = 2 x3,14
/ 86164 ~7,29 10-5 rad s-1.
2.
Exprimer la vitesse v du lanceur dans le référentiel géocentrique en
fonction de sa latitude l,
du rayon terrestre R et de W.
3. Quelles
latitudes faut-il privilégier pour le site de lancement ? Justifier.
Du fait de la rotation de la terre, la vitesse initiale de la fusée est
maximale à l'équateur ( l
= 0 et cos 0 = 1). Cette vitesse vient s'ajuter à celle imprimée par le
lanceur.
II. Décollage.
Le premier étage est un étage cryogénique. Il contient deux réservoirs,
l'un de dioxygène et l'autre de dihydrogène, maintenus tous deux à
l'état liquide. Injectés dans la chambre de combustion, la réaction de
ces deux composés chimiques conduit à la formation de vapeur d'eau qui
s'échappe par la tuyère du moteur et propulse le lanceur.
4. Sur quel principe repose la propulsion du
lanceur ?
La propulsion par réaction est basée sur le principe d'action-réaction.
La conservation de la quantité de mouvement du système ( fusée + gaz
éjectés) implique que l'éjection des gaz vers l'arrière, transmet par
réaction une poussée à la fusée vers l'avant.
5. Déterminer les
quantités de matière de dioxygène et de dihydrogène contenues dans les
deux réservoirs du premier étage.
840 tonnes de dioxygène et 140 tonnes de dihydrogène.
n(O2 ) = 8,4 108 / 32 = 2,625 107
~2,63 107 mol ; n(H2) = 1,40 108 / 2 =
7,0 107 mol ( en excès).
6.
Ecrire l'équation modélisant cette transformation chimique.
O2(g) + 2H2(g) ---> 2H2O(g).
7. Déterminer la
masse maximale de vapeur d'eau qui s'échappe pendant la durée de
propulsion du premier étage.
n(H2O) = 2 n(O2) =5,25 107 mol.
m(H2O) = 5,25 107 x 18 =9,45 108
g ~9,45 102 tonnes.
8.
En supposant que le débit massique de vapeur d'eau du premier étage est
constant, montrer que sa valeur est qm = 1,97 103
kg s-1. En déduire la valeur de la poussée du premier étage.
La durée de combustion est égale à 480 s.
qm =9,45 108 / 480 ~ 1,97 106
g s-1 =1,97 103 kg s-1.
L'impulsion spécifique (Isp) des ergols est égale à 360 s. Cette
impulsion spécifique indique la durée pendant laquelle le moteur
fournit une poussée égale au poids sur terre des gaz éjectés.
Isp = F / (qm g) ; F = Isp qm g = 360 x1,97 103
x 9,81 ~6,96 106 N = 6,96 103 kN.
9. Quelle est
l'accélération initiale du lanceur si les deux boosteurs et le premier
étage s'allument ensemble à l'instant t = 0 ? Commenter la valeur
obtenue.
La poussée de chaque booster est de 16 000 kN. Masse de la fusée au
lancement : 2700 tonnes.
La fusée est soumise à son poids, verticale, vers le bas et et à la pousée
totale, verticale vers la haut.
a = (poussée totale - poids) / masse totale = (3,2 107+6,96
106-2,7 106x9,81) / (2,7 106)~4,62 m s-2.
Cette valeur est voisine de la moitié de l'accélération de peanteur
terrestre au niveau du sol
|
|
|
III. La
phase de vol vertical.
Durant
la première phase de vol ( avant le détachement des boosters), à
l'instant t, la masse du lanceur est m(t) et sa vitesse v(t). Les
propulseurs d'appoint éjectent des gaz à la vitesse ve
supposée constante par rapport au lanceur.
On note dmg la masse de gaz ejectés par le lanceur entre les
instants t et t +dt et on définit le débit massique qm = dmg
/ dt = -dm / dt. On note d
= qm / m0 ( m0 : masse initiale du
lanceur).
Le débit massique est considéré comme constant. Une fois la totalité
des gaz éjectés au bout de la durée T, le lanceur atteint sa vitesse
finale vf et sa masse mf et les boosters sont
détachés.
Hypothèses
: le lanceur a un mouvement rectiligne vertical jusqu'au détachement
des boosters ; les effets de l'air et la variation de l'intensité de la
pesanteur avec l'altitude sont négligeables.
10. Exprimer m(t)
en fonction de m0, d
et t.
m(t) = m0 -dmg = m0-qmdt =m0-m0
d dt=m0(1-d dt).
L'équation de Tsiolkovski corrigée s'écrit : v(t) = v0 + ve
ln(m0 / m(t)) -gt.
11. Commenter l'expression de cette
équation corrigée.
Dans l'équation, Dv = v(t) -v0 = ve
ln( m0 / m(t)),
la fusée n'est soumise qu'à la force de poussée
fournie par son moteur. Elle ne tient compte d'aucune autre action
extérieure. L'équation corrigée prend en compte l'attraction terrestre.
12.
Exprimer vf en fonction de g, T, ve, m0
et mf.
vf = v0 + ve
ln(m0 / mf) -gT.
3.
Sur quels paramètres peut-on agir pour avoir la vitesse de fin de
propulsion la plus élevée possible ?
On peur faire croître ve et diminuer T.
On admet que l'altitude de la fusée peut se mettre sous la forme :
z(t) = -½gt2 +v0t +ve / d [-m(t) / m0 ln
(m0 / m(t)) +dt]
+z0.
14. Déterminer la
vitesse d'éjection des gaz à la sortie d'un booster.
ve = Isp g =270 x9,81 ~2,65 103 m /s.
15. Déterminer les valeurs de vf
et l'altitude hf atteintes juste avant le détachement des
boosters.
vf
= v0 + ve ln(m0 / mf) -gT.
Les boosters consomment en premier leur propergol ( soit 2 x 630
t) durant T =130 s.
m0 = 2700 t ; mf = 2700-2 x 630)=1440 t ; v0
= 0, la fusée est initialement immobile.
vf = 2,65 103 ln(2700 / 1440)-9,81 x130 ~3,91 102
m s-1.
Débit massique des gaz des 2 boosters : poussée / ve = 2
x1,6 107 / (2,65 103)=1,207 104 kg s-1.
d =qm
/ m0 =1,207 104 / (2,7 106) =4,47 10-3
s-1.
zf = -0,5
x9,81 x1302+2,65 103 /(4,47 10-3)
[-1,44 /2,7 ln(2,7 /1,44)+4,47 10-3 x130] = 6,31 104
m ~63 km.
16. Quelles
influence sur les valeurs de vf et zf les
hypothèses formulées ont-elles ?
L'action de l'air diminue la vitesse de la fusée ; g varie peu sur une
altitude inférieure à 60 km, mais diminue ensuite ( ce qui augmente la
vitesse calculée et l'altitude atteinte).
17. D'un point de
vue qualitatif, quel est l'intérêt d'une fusée à plusieurs étages ?
La fusée à étages s'allège en larguant les réservois vides. Chaque
étage démarre avec la vitesse initiale donnée par l'étage précédent.
Une fusée à un seul étage ne pourrait pas atteindre la vitesse minimum
de satellisation.
IV. Mise en orbite du
module d'exploration autour de la terre.
Un module placé en orbite circulaire autour de la terre à une altitude
h = 5800 km pourra accuillir jusqu'à 4 astronautes et effectuer des
rendez-vous avec des modules de plus grande capacité non encore
développés, destinés à faire le trajet vers Mars.
18. Une fois le
deuxième étage détaché, en négligeant tout frottement du milieu
interstéllaire et l'attraction des autres astres que la terre, on peut
supposer que le module de masse m, en orbite circulaire de rayon r
autour de la terre, est soumis à une force unique conservative. A
quelle force est soumis le module. Rappeler son expression et faire un
schéma de la situation.
Le module est soumis à la force de gravitation attractive excercée par
la terre.
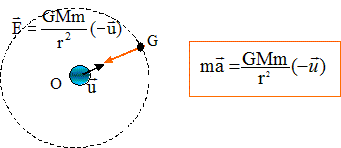
19. Comment peut être qualifiée
l'accélération ? Donner son expression en fonction de G, M R et h puis
calculer sa valeur.
L'accélération est centripète.
a = MG /(R+h)2 =5,98 1024 x 6,67 10-11
/ (6,370 106 +5,8 106)2=2,69 m s-2.
20. En déduire
l'expression de la vitesse v1 du module d'exploration en
fonction de G, M, R et h. Calculer sa valeur.
v1 = [GM / (R+h)]½ =[6,67 10-11 x5,98
1024/
(6,370 106 +5,8 106)]½ =5,72 103
m s-1.
Une fois en orbite, le module d'exploration devra mettre en route
d'autres moteurs pour se libérer de l'attraction terrestre et se
satelliser autour de Mars.
21. Rappeler la
définition de l'énergie mécanique d'un point matériel et en déduire la
valeur de la vitesse de libération v2 que devra atteindre le
module depuis son orbite terrestre à l'altitude h = 5800 km pour
échapper à l'attraction terrestre.
L'énergie mécanique est la somme de l'énergie potentielle et de
l'énergie cinétique.
E = ½mv2 -GMm/(R+h).
La vitesse de libération est la vitesse qui parmet au satellite
d'échapper à l'attraction terrestre et de parvenir en un point
infiniment éloigné du centre de la terre avec une vitesse nulle.
½mv22
-GMm/(R+h) = 0.
v22 =2GM / (R+h) ; v2
= [2GM / (R+h)]½=[2 x6,67 10-11
x5,98 1024/ (6,370 106 +5,8
106)]½ ~8,1 103 m s-1.
|
|
|
|
V. Orbite de trransfert.
La
trajectoire consommant le moins d'énergie est une orbite elliptique
tangente aux deux orbites coplanaires. Le module initialement en orbite
autour de la première planète effectue une trajectoire elliptique,
appelée orbite de transfert de Hohmann, dont le soleil est l'un des
foyers, jusqu'à se positionner sur une orbite coplanaire autour de la
seconde planète.
22. On
ne prend en compte que l'attraction solaire sur le module. Le module
décrit une trajectoire de transfert de Hohmann depuis la terre
jusqu'aux abords de Mars. Déterminer l'angle terre-soleil-mars au
moment de l'allumage des fusées du module lorsqu'il est encore en
orbite autour de la terre et le temps que mettra ce module pour
parcourir la trajectoire de Hohmann.
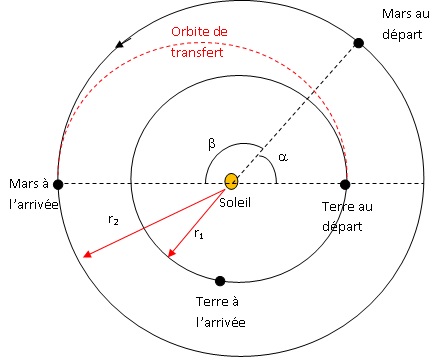
On suppose que les deux planètes décrivent un mouvement circulaire et
uniforme pendant le temps du voyage.
Le satellite parcourt la moitié
de l'ellipse de transfert. La durée du parcours est la moitié de la
période de révolution T sur l'ellipse. La troisiéme loi de Kepler donne
la période T en fonction de r1 et r2.
T2 =4 p2
((½1+½r2)3 / (GMSoleil )=4
x3,142(75 109 +114 109)3 /
(6,67 10-11 x1,99 1030) ~2,0 1015 ; T
~ 4,5 107 s ; ½T =2,24 107 s ou 259 jours
ou environ 0,71 an.
La 3ème loi de Kepler appliquée à Mars conduit à : Mars accomplit
une orbite complète de 360° en 1,88 an.
Durant cette durée Mars décrit l'angle ß =
0,71 *360 / 1,88 = 135°.
a+ß = 180° d'où a = 180-135 ~45°.
|
|
|