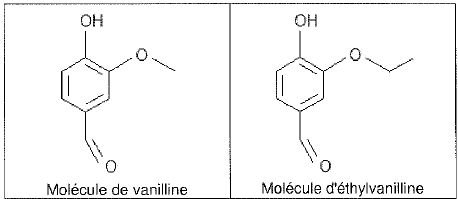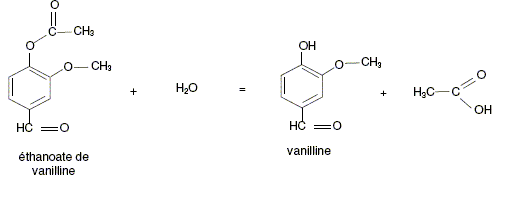
La vanilline, glaçon à la surface de l'eau, concours Geipi Polytech 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . La vanilline.   1. Donneer la formule brute de la vanilline. C8H8O3. La dernière étape de la synthèse est décrite ci-dessous. 2. Donner le nom et la formule de l'autre produit que la vanilline. L'acide éthanoïque CH3-COOH. 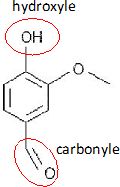3. Entourer les deux fonctions chimiques présentes dans la molécule de  vanilline et les nommer. Fonction alcool : OH ; fonction aldehyde : carbonyle. 4. La vanilline existe sous la forme d'un coupla acide base noté VanOH /VanO- de pKa = 7,4. Représenter les deux formes de ce couple sur un diagramme de prédominance 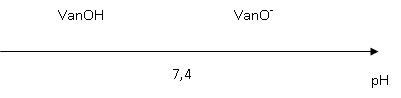. On se propose de doser la vanilline présente dans du sucre vanilllé commercial par spectrophotoùétrie. On prépare dans un premier temps des solutions étalon par dissolution de vanilline dans une solution aqueuse de soude de concentration 0,10 mol/L. 5. Donner le pH de cette solution de soude. La soude est une base forte : pH = 14 + log c = 14 + log 0,10 = 13. On réalise le spectre de chaque étalon. L'absorbance est mesurée au maximum d'absorption en fonction de la concentration en vanilline. La solution S est préparée  en dissolvant la vanille extraite de m = 1,00 g de sucre vanillé dans V = 100,0 mL de la solution de soude précédente. 7. Dans quel domaine du spectre électromagnétique la vanilline absorbe t-elle ?. Le maximum d'absorption appartient au domaine UV. 8. Donner la concentration molaire en vanilline de S.  L'absorbance de cette solution S est A = 1,2. CS = 45 µmmol / L. 9. Déterminer la masse de vanilline contenue dans 1,00 g de sucre vanillé M(vanilline )= 152 g/mol.. 4,5 µmol dans V = 100,0 mL soit 4,5 x152 = 6,84 102 µg = 0,684 mg. Un glaçon flotte à la surface de l'eau liquide dans un verre. Un glaçon a la  forme parallèlépipè rectangle de hauteur h. Sa base horizontale est un rectangle d'aire S. On note V = S h son volume. Le glaçon est immergé dans l'eau sur une hauteur h2 et émerge sur une hauteur h1 : h = h1 +h2. Il est soumis à son poids P=Mg=rsol Vg et à la poussée d'Archimède F = rliq V2g. On note C le centre de gravité du glaçon. m : masse du glaçon ; V1 volume de la partie émergée ; V2 : volume de la partie immergée du glaçon. rliq = 1000 kg m-3 ; rsol = 920 kg m-3 ; 1. Rappeler la loi qui régit l'équilibre du glaçon dans l'eau. 1ère loi de Newton : A l'équilibre, le poids et la poussée d'Archimède se compensent. Le glacon est pseudo-isolé et il est soit immobile ( si sa vitesse initiale est nulle) soit animé d'un mouvement rectiligne uniforme ( si sa vitesse initiale n'est pas nulle ). 2. Quel est le point d'application de la force F ? La poussée d'Archimède s'applique au centre du volume de liquide déplacé. 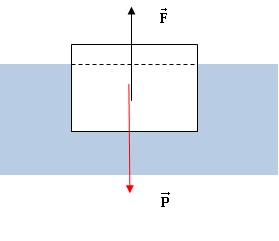1. Ecrire la relation reliant le rapport r = h1 / h2 et le rapport des masses volumiques rliq / rsol. Calculer ce rapport en pourcentage. A l'équilibre : rsol (V1+V2)g = rliq V2g. rsol (h1+h2)S = rliq h2S. rsol (h1+h2) = rliq h2. (h1+h2) / h2 = rliq / rsol . h1 / h2 =rliq / rsol -1 =1000 / 920 -1 ~0,087 (8,7 %). . . Le glaçon est déplacé et maintenu au fond du verre. Il est soumis à son poids P = Mg et à une nouvelle poussée d'Archimède F' = rliq Vg. A l'instant t=0, le glaçon est libéré et remonte vers la surface. On considérera que le glaçon est toujours immergé et on négligera les frottements. On note z l'axe vertical, positif vers le haut, d'origine z = 0 en C au fond du verre. 4. Ecrire la relation liant az, P et F'. La seconde loi de Newton écrite sur l'axe z donne : Maz = F' -P ; az = F' / M -g. 5. En déduire l'expression littérale de az en fonction de g, rliq et rsol. az = rliq Vg / ( rsol V) - g =g( rliq  /  rsol -1). 6. En déduire l'expression littérale de z en fonction du temps. v(t) =azt, la vitesse initiale étant nulle. z(t) = ½azt2, la position initiale étant l'origine de l'axe. 7. Calculer le temps t1 nécesaire au glaçon pour remonter dans le verre d'une hauteur de 10 cm. az = 9,81 ( 1000 / 920 -1) =0,853 m s-2. t1 =(2 x0,10 / 0,853)½ ~0,48 s.

menu