Géométrie,
nombres complexes, concours Geipi Polytech 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Géométrie dans l'espace.
Les affirmations suivantes sont-elles vraies ?
Partie A.
On considère deux plans P1 et P2 donnés par leur équation cartésienne respective :
2x +3y +4z-1 = 0 et x+2y+z=0.
1. Le vecteur n de coordonnées (1 ; 1,5 ; 2 ) est un vecteur normal du plan P1. Vrai.
Coordonnées d'un vecteur normal au plan P1 : (2 ; 3; 4) soit k ; 1,5 k ; 2k) avec k réel.
2. Les deux plans sont parallèles. Faux.
Coordonnées d'un vecteur normal au plan P2 : (1 ; 2 ; 1).
Les deux vecteurs normaux à ces deux plans ne sont pas colinéaires : les plans ne sont pas parallèles.
3. Les deux plans
sont sécants et leur intersection est une droite de vecteur directeur u
dont les coordonnées sont ( -5 ; 2 ; 1). Vrai.
Soit M ( x ; y ; z) appartenant à l'intersection des plans.
2x +3y +4z-1 = 0 et x+2y+z=0.
x = -z-2y.
Par suite : -2z-4y +3y +4z-1 = 0 ; -y +2z-1 = 0 ; y = 2z-1 et x = -5z+2.
Equation paramétrique de la droite intersection des plans : x = -5 t+2 ; y = -1+2t ; z=t.
Partie B
On note R, S, T et U les points de coordonnées respectives : R(2 ; 4 ; 1) ; S (0; 4 ; -3) ; T(3 ; 1 ; -3) ; U (1 ; 0 ; -2).
Soit P le plan d'équation cartésienne : 2x +2y -z -11 = 0.
1. Les points R, S et T appartiennent à un plan de vecteur normal ( 2 ; 2 ; -1). Vrai.

2. La droite (TU) est orhogonale à la droite (RS) et admet la représentation paramétrique :
x = -1+2t ; y = -1+t ; z = 1-t, avec t réel. Faux.
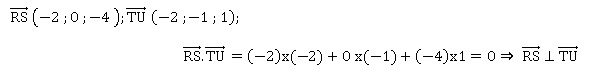
U appartient à la droite (TU) d'où une représentation paramétrique de cette droite :
x = 1-2t ; y = -t ; z = -2+t.
3 Le point V(3 ; 2 ; -1) est le projecté othogonal du point U sur le plan P. Faux.

Partie C.
Soient deux droites D1 et D2 données par un système d'équations paramétriques.
D1 : x = 1+t ; y = t ; z = -5+t ; D2 : x = 8 +k ; y = 4+k ; z = -3; t et k réels.
On note Q le plan d'équation : 2x-3y +2z = 0.
1. Le vecteur u de coordonnées ( 1 ; 1 ; 1) est un vecteur directeur de la droite D1. Vrai.
2. La droite D2 passe par le points de coordonnées (5 ; 1 ; -3). Vrai.
5 = 8 +k soit k = -3 ; par suite y =1 = 4-3 ; z = -3 .
3. Soient M un point qe D1 et N un point de D2 de coordonnées respectives M(1+t ; t ; -5+t) et N(8+k ; 4+k ; -3).
La droite (MN) est parallèle au plan Q si et seulement si t+k=6. Vrai.
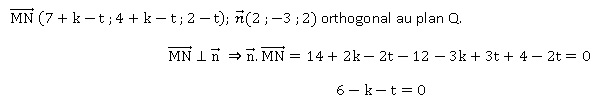
|
|
|
Partie D.
On considère un cube dont les arètes sont de longueur 1. I et J sont les milieux respectifs de [AB] et [CG].
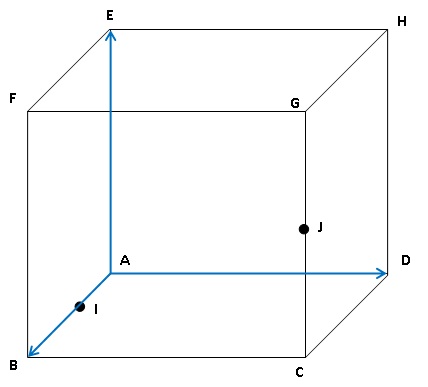
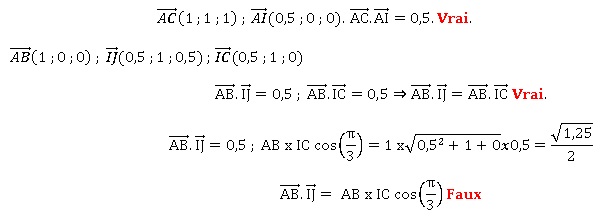
Nombres complexes.
Partie A. a désigne un nombre réel.
On considère les complexes suivants :
z1 = (-4a+i) ( a-i) -(1+2ai)2.
z2 = (2+2ai) / (1-i) ; z3 = 2*3½-2i ; z4 = -exp(ip / 5).
1. Déterminer la forme algébrique de z1.
z1 = -4a2+1+5ai-(1-4a2+4ai)= ai.
2. Déterminer la forme algébrique de z2.
(2+2ai)(1+i) / (1+1)=(2-2a+i(2a+2)) / 2 = 1-a +i(a+1).
3. Déterminer le module et l'argument de z3.
|z3| =(12+4)½ = 4 ; z3 / |z3| = 3½/ 2 -0,5 i = cos(-p/6 )+ i sin (-p/6).
4. Déterminer la forme exponentielle de z4.
exp(ip) x exp(ip / 5) =exp(6ip / 5).
Partie B. Soit x un réel strictement positif. On considère les points A, B et C d'affixes respectives :
zA =1-xi ; zB = 2i et zC = -2.
1. Donner les distances AB et AC en fonction de x.
AB = ((0-1)2 +(2+x)2)½ =(1+4+4x+x2)½ =(5+4x+x2)½ .
AC = ((-2-1)2 +x2)½ =(9+x2)½.
2. Pour quelle valeur de x le triangle ABC est-il usocèle en A ? Justifier.
AB = AC ; 5+4x+x2=9+x2 ; 5+4x = 9 ; x = 1.
3. Le triangle ABC peut-il être équilatéral ? Justifier.
AB = AC, alors x = 1 et AC = 10½.
BC = ((-2)2 +22)½ = 8½, valeur différente de AC. Le triangle ABC ne peut pas être équilatéral.
4. Soit D le point tel que ABCD soit un parallélogramme. Déterminer en fonction de x, l'affixe zD du point D. Justifier.
Les diagonales du parallèlogramme sont égales :
zD-zA = zC-zB avec zD = a +ib, a et b réels.
1-a - i(x+b) =2+2i.
On identifie : 1-a = 2 soit a = -1 et -x-b = 2 soit b = -x-2.
zD = -1 -i(x+2).
.
|
|
|
|
|
Partie C.
1. Déterminer l'ensemble F1 des solutions dans C-{-4} de l'équation (E1) (z+2) / (z+4) = z+3. Justifier.
z+2 = (z+3) (z+4) ; z+2 = z2+12+7z ;
z2 + 6z +10 = 0. D = 62-4x10 = -4 = 4 i2.
Solutions : (-6+2i/ / 2 = -3+i et -3-i.
Partie D.
1. Déterminer l'ensemble F2 des solutions dans C de l'équation (E2) 2iz-1 = conjugué de z+i. Justifier.
z = x + iy ; conjugué de z : x-iy.
2iz-1 =2i(x+iy) -1 = 2ix+2i2y-1 =2ix-2y-1.
Conjugué de z+i = x-iy+i = x+i(1-y).
On identifie partie imaginaire et partie réelle :
2x = 1-y et x= -2y-1 ; -4y-2 = 1-y soit y = -1 et x = 1 ; z = 1-i.
Partie E.
On considère les points E, F et G d'affixes respectives : zE = i ; zF = -2 et zG = 4i.
1. Donner sans justification, l'ensemble F3 des points M d'affixe z tels que |z-i| = 2.
|z-i|=EM = 2.
F3 est le cercle de centre E et de rayon 2.
2. Donner sans justification, l'ensemble F4 des points M d'affixe z tels que |z+2| = |z-4i|.
|z+2| =FM ; |z-4i| =GM.
F4 est la médiatrice du segment [FG]
|
|
|