QCM
mathématiques, école de santé des armées,
concours ESA 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Exercice 1. Une seule affirmation est exacte.
1. La fonction f est définie sur R par f(x) = e-x-x+1. l'image de ln (2) par la fonction f est
A) 0,5 -ln(3).
f(ln2) = e-ln(2) -ln(2) +1 =1 / eln(2) -ln(2) +1 =1 / 2 -ln(2) +1 = 1,5 -ln(2).
B) -1-ln(2)
C) 1,5 -ln(2). Vrai..
D) 3 1-ln(2).
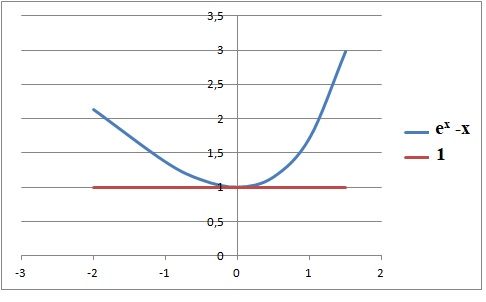
2. Sur R, l'inéquation ex-x < 1 admet pour ensemble de solutions :
A) aucune solution.
B) zéro. Vrai.
C) [0 ; + oo[.
D) L'ensemble des réels.
3. On considère la fonction f définie sur R par f(x) = x e-x. Une primitive F de la fonction f sur R est définie sur R par :
A) F = -0,5 x2 e-x.
On dérive en posant u = -0,5 x2 et v = e-x ; u' = -x ; v' = -e-x.
u'v +v'u = -xe-x+0,5x2e-x.
B) F = -(1+x)e-x. Vrai.
On dérive en posant u = -(1+x) et v = e-x ; u' = -1 ; v' = -e-x.
u'v +v'u = -e-x+(1+x)e-x=x e-x.
C) F =-xe-x.
On dérive en posant u = -x et v = e-x ; u' = -1 ; v' = -e-x.
u'v +v'u = -e-x+xe-x.
D) F = (1-x)e-x.
On dérive en posant u = (1-x) et v = e-x ; u' = -1 ; v' = -e-x.
u'v +v'u = -e-x+(1-x)e-x= -x e-x.
4. Pour Pour tout x, l'expression A(x) = (ex+e-3x) / e2x -(1-e-2x) /ex est égale à :
A(x) = (1+e-4x) / ex -(1-e-2x) /ex =(e-4x+e-2x) / ex= e-5x+e-3x=(1+e2x) / e5x.
A) (e2x+1) / e3x.
B) e3x(e-2x+1).
C) (e2x+1) / e5x. Vrai.
D) e-5x-e-3x.
5. La limite en x= 3 de l'expression C=[ (x+6)½ -3] / (x-3) est égale à :
On pose A=(x+6)½ et B = 3 ; A-B = (A2-B2) / (A+B) ;
[ (x+6)½ -3] = [(x+6) -9] / [ (x+6)½ +3] =(x-3) / [ (x+6)½ +3] ; C = 1 / [ (x+6)½ +3]
Quand x tend vers 3, C tend vers 1 / 6.
A) zéro ; B) plus l'infini ; C) 1 ; D) 1 / 6. Vrai.
6.La fonction f est définie sur ]0 ; + oo{ par f(x) = (x-3) ln(x) est :
A) f(x) est positive sur cet intervalle. Faux.
f(2) = -ln(2) < 0.
B) f(x) est négative sur cet intervalle. Faux.
f(4) = ln(4) >0.
C) négative sur ]0 ; 1 ]. Faux.
(x-3) est négatif et ln(x) est négatif sur ]0 ; 1 ].
D) positive sur [3 ; + oo[. Vrai.
(x-3) est positif ou nul et ln(x) est positif sur [3 ; +oo [.
7. Soit la fonction f définie sur ]0 ; + oo[ par f(x) = (x-3) ln(2x). Sa fonction dérivée est définie sur cet intervalle par :
on pose u = x-3 et v = ln(2x) ; u' = 1 ; v' = 1 / x ; u'v +v'u = ln(2x) + (x-3) / x.
A) ln(2x) -(x-3) / (2x).
B) ln(2x) +(x-3) / x. Vrai.
C) 1 /x.
D) 1 / (2x)
8. Soit la fonction f définie sur ]2,5 ; + oo[ par f(x) = (-2x+5)-4.
Une primitive de f(x) sur cet intervalle est :
A) F(x) =( --2x+5)-5/5. Faux.
L'exposant de ( --2x+5) dans F(x) doit être égal à -3.
B) (-2x+5)-5 / 10. Faux.
C) (-2x+5)-3 / 6. Vrai.
On dérive en posant u = -2x+5 ; u' = -2 ; dérivée de u-3 = -3u' u-4 = 6(-2x+5)-4.
Dérivée de (-2x+5)-3 / 6 = (-2x+5)-4 = f(x).
D) (-2x+5)-3 / (-3).
|
|
|
|
Exercice 2. Une seule des affirmations est exacte.
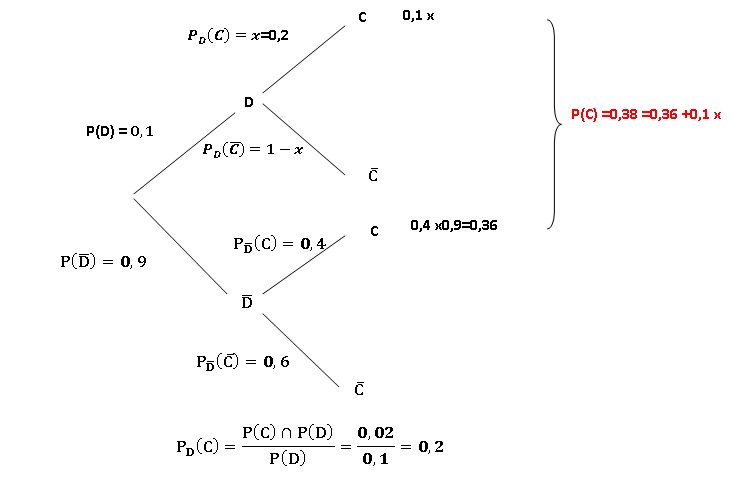
9)
Une documentaliste a reçu une offre pour acheter les romans
de la saga HP. Elle enquète pour savoir si le sujet intéresse les
élèves et relève que :
10 % des élèves ont lu le 7è épisode ;
38 % des élèves ont vu le 7è épisode au cinéma ;
40 % de ceux qui n'ont pas lu, on vu le 7è épisode au cinéma.
La documentaliste prend au hasard une réponse parmi celles des élèves interrogés.
La probabilité que l'élève soit allé voir le 7è épisode au cinéma sachant qu'il la lu est :
A) 0,3 ; B) 0,2 Vrai; C) 0,038 ; D) 0,4.
On note D l'événement " l'élève a lu le 7è épisode" et C l'événement " l'élève a vu le 7 è épisode au cinéma".
10)
Un élève se présente à deux concours C et C' qui sont indépendants. Il
a une chance sur 3 de réussir le concours C et une chance sur 3 de
reussir le concours C'. En pensant augmenter ses chances de réussite,
l'élève décide de passer les deux concours. La probabilité qu'il
réussisse au moins un concours est :
A) 2 / 3 ; B) 1 /9 ; C) 4 / 9 ; D) 5 / 9. Vrai.
Probabilité de n'être pas reçu : 2 /3 x 2 / 3 = 4 / 9.
Probabilité d'être reçu à 1 ou 2 concours 1 - 4 /9 = 5 / 9.
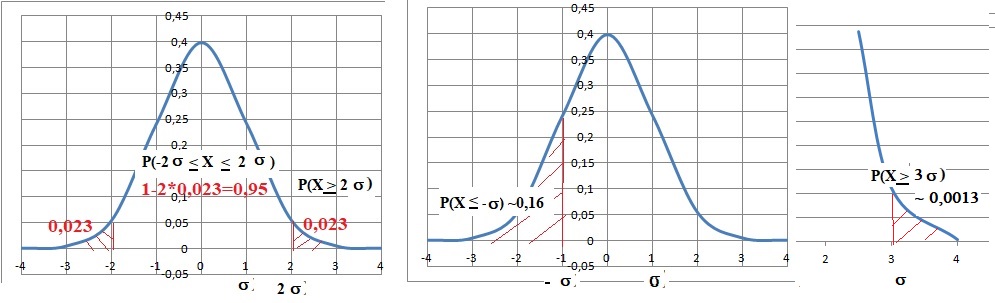
11) Soit X une variable aléatoire qui suit la loi normale N( 0 , s2). Alors on a :
A) P(-2s < X < 2s) ~0,99 ;
B) P( X > 3s) ~0,005 ;
C) P( X < -s) ~0,6 ;
D) P( X > 2s) ~0,0025.
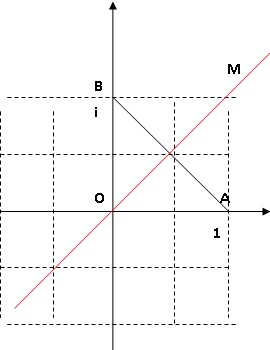
12. Le plan complexe est muni d'un repère orthonormé direct d'origine O. Les points A et B ont pour affixe respective i et -1. L'ensemble des points M d'affixe z vérifiant |z-i| = |z+1| est :
A) la droite AB.
B) Le cercle de diamètre AB.
C) La droite perpendiculaire à AB passant par O. Vrai.
D) Le cercle de diamètre [AB] privé de A et B.
AM = |z-i| ; BM = |z+1 ; AM = BM. M appartient à la médiatrice du segment AB.
13) Sur l'intervalle [0 ; 2p], l'équation 2 sin2 x - sin x -1 = 0 :
A) n'admet pas de solution
On pose X = sin (x) avec -1 < X < 1 ; 2X2-X-1 = 0 ; discriminant D =(-1)2+4x2 =9 ;
solutions X = (1 +3) / 4 = 1 et (1-3) / 4 = -0,5.
sin(x) = 1 soit x = p / 2 ; sin(x) = -0,5 soit x = -p / 6 et 7p/6.
B) admet deux solutions.
C) trois solutions. Vrai.
D) admet une infinité de solutions.
|
|
|
|
|
Exercice 3.
La
durée d'attente exprimée en heures, au services des urgences peut être
modélisée par une variable aléatoire T qui suit une loi exponentielle
de paramètre l positif.
Partie A.
1) Interpréter graphiquement la probabilité P(T < 1).
2) Indiquer où peut être lu graphiquement le paramètre l.
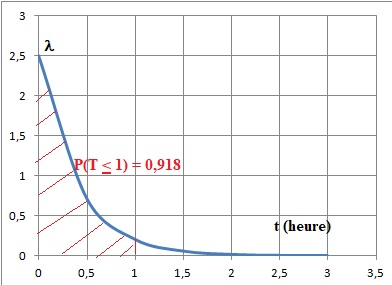
Dans la suite P(T) < 1) = 0,92 et e-2,5 ~0,08.
Partie B.
1. Déterminer la valeur exacte de l. Dans la suite on prendra l = 2,5.
P (T < 1) = 1 -e-l = 0,92 ; e-l =0,08 ; l = -ln(0,08).
2. Calculer P(1 < T < 2 ) à 10-2 près.
P (T < 2) = 1 -e-2l ; P(1 < T < 2 ) = 1 -e-2l -0,92 = 0,08-e-5 ~0,08-0,0067 ~0,07.
3. Calculer P( T > 2 ) à 10-2 près.
P(T >2) = 1-P(T < 2) = 1-(1 -e-2l )= e-5 ~0,0067 ~0,007.
|
|
Partie C.
Un questionnaire est distribué aux patients.
Si la durée est inférieure à 1 heure, ils cochent la case " attente satisfaisante" ;
si la durée est comprise strictement entre 1 heure et 2
heures, 80 % cochent la case "attente satisfaisante" et 20 %
cochent la case " attente non satisfaisante" ;
si la durée d'attente est supérieure ou égale à 2 heures, ils cochent la case " attente non satisfaisante".
On prélève de façon aléatoire un questionnaire.
1.a calculer la probabilité de lire " attente satisfaisante".
|
|
satisfaisant
|
non satisfaisant
|
P (T < 1)
|
0,92
|
0,92
|
0
|
| P(1 < T < 2 ) |
0,0733
|
0,8 x0,0733 = 0,0586
|
0,2 x0,0733 = 0,0147
|
| P( T > 2 ) |
0,0067
|
0
|
0,0067
|
Probabilité de lire " attente satisfaisante" : 0,92 +0,0586 = 0,9786 ~0,98.
1.b.
Sachant que la case cochée est " attente satisfaisante", calculer la
probabilité qu'elle provienne d'un patient ayant attendu entre 1 h et 2
h strictement.
0,0586 / 0,9786 ~0,060.
2.
On prélève deux questionnaire. Calculer la probabilité, qu'au moins un
patient ait coché la case " attente non satisfaisante".
Au moins 1 signifie 1 ou 2.
En tirant deux questionnaires, probabilité que deux patients cochent " satisfaisant" : 0,9786 x 0,9786 = 0,9576.
Probabilité, qu'au moins un
patient ait coché la case " attente non satisfaisante". 1-0,9576 ~0,04.
|
|
|