Physique,
concours ENSM 2018
Formation des ingénieurs de l'école normale supérieure maritime
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Bataille navale ( 7 pts).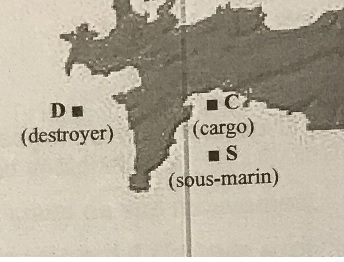
Le capitaine S et le commandant D ont pour mission de couler le cargo C.
Partie 1. Tir du sous-marin.
SC = d = 3,2 km.
Le sous-marin tire une torpille dans l'axe du cargo à une vitesse v0 = 20,0 m /s. Elle se propage horizontalement, avec un mouvement rectiligne uniforme, juste sous la surface de l'eau.
1.1. Justifier que la torpille se déplace sur un axe horizontal par un schéma et par un calcul.
La torpille est soumise à son poids P, verticale vers le bas, à la
poussée d'Archimède F, verticale vers le haut, à la force
propulsive F ' de son moteur électrique et au frottement fluide f.
P = mg = 1,31 103 x9,81 = 1,29 104 N.
F = VT reau g = 1,18 x1,11 103 x9,81 =1,28 104 N.
Le poids et la poussée se neutralisent.
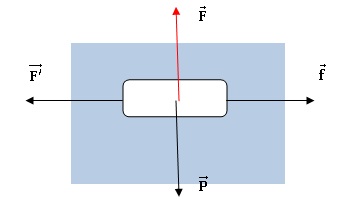
1.2. Justifier sans calcul la nature du mouvement.
Le mouvement est rectiligne uniforme d'après l'énoncé.
1.3. Calculer la durée du tir.
t = d / v0 = 3200 / 20,0 = 1,6 102 s.
Partie 2. Tir du destroyer.
DC = L = 13,5 km.
L'obus par de D avec une vitesse de valeur v0 = 725 m /s, inclinée de l'angle a = 7,30° par rapport à l'horizontale. L'obus touche la mer en C.
Masse de l'obus m = 4,44 kg. On néglige les frottements.

2.1.a. Faire le bilan des forces appliquées à l'obus entre D et C.
L'obus n'est soumis qu'à son poids, verticale, vers le bas, valeur mg. Le mouvement est une chute libre.
2.1.b. Etablir l'expression du vecteur accélération de l'obus.
La seconde loi de Newton conduit à : ax = 0 ; ay = -g.
2.1.c. Montrer que les équations horaires du mouvement de l'obus sont : x(t) = v0 cos a t et y(t) = -½gt2 +v0 sin a t.
La vitesse est une primitive de l'accélération et la vitesse initiale a pour coordonnée ( v0 cos a ; v0 sin a ).
Vecteur vitesse : ( v0 cos a ; -gt+v0 sin a ).
La position est une primitive de la vitesse et la position initiale est l'origine du repère.
x(t) = v0 cos a t et y(t) = -½gt2 +v0 sin a t.
2.1.d. En déduire l'équation de la trajectoire de l'obus. ( expression littérale).
t = x(t) / v0 cos a ; repport dans y(t) :
y(x) = -½gx2 / ( v0 cos a)2+ tan a x.
2.1.e. Montrer que y(x) = -9,48 10-6x2 +0,128x.
y(x) =-0,5 x9,81 x2 / ( 725 cos 7,3)2+ tan 7,3 x.
y(x) = -9,48 10-6x2 +0,128x.
2.2.a. Montrer que le tir atteint le cargo C.
yC=0 = -9,48 10-6x2 +0,128x= x ( -9,48 10-6 x+0,128).
x = 0, position initiale ; x = 0,128 / (9,48 10-6) = 1,35 104 m = 13,5 km ( position de C).
|
|
La montagne.
Le
cargo s'abrite derrière une montagne située à d = 9,20 km du destroyer
et elle culmine à une hauteur H = 480 au dessus de l'eau.
2.2.b. Vérifier par un calcul si l'obus passe au dessus de la montagne.
y(d) = -9,48 10-6d2 +0,128d.
y(d) = -9,48 10-6x 92002 +0,128 x 9200 =375 m, valeur inférieure à H.
L'obus frappe la montagne.
Le destroyer a le temps d'armer un second tir. Il oriente son canon de
manière à passer au dessus de la montagne. Il choisit un angle a' = 82,7°.
2.2.c Montrer que le tir est réussi.
y(x) =-0,5 x9,81 x2 / ( 725 cos 82,7)2+ tan 82,7 x.
y(x) = -5,78 10-4x2 +7,81x.
yC=0 = -5,78 10-4x2 +7,81x= x ( -5,78 10-4 x+7,81).
x = 0, position initiale ; x = 7,81 / (5,78 10-4) = 1,35 104 m = 13,5 km ( position de C).
On considère que les tirs consécutifs se font sans perte de temps.
2.2.d. Calculer la durée qui s'écoule avant que le destroyer touche le cargo.
Premier tir : t = x(t) / v0 cos a =1,35 104 /(725 cos7,3) =18,8 s.
Second tir : t = x(t) / v0 cos a =1,35 104 /(725 cos82,7) =146,5 s.
Durée totale avant de toucher le cargo : ~165 s.
2.2.e. Montrer que son erreur lui coûte la partie.
La torpille atteint le cargo au bout de 160 s.
L'obus atteint le cargo au bout de 165 s.
Exercice 2. Le bateau de croisière.
Partie 1.La piscine chauffée.
Il utilise une pompe à chaleur (PAC) air - eau. La température de l'air extérieur est q1 = 14°C. La piscine étant couverte, on néglige les échanges thermiques avec l'extérieur. La température initiale de l'eau est q2 = 14°C avant chauffage.
1.1. Identifier la source chaude et la source froide.
La source froide est l'air extérieur et la source chaude est l'eau de la piscine.
1.2. Faire
apparaître sur un diagramme énergétique, le sens des transferts
thermiques entre la PAC, les sources et le réseau électrique.
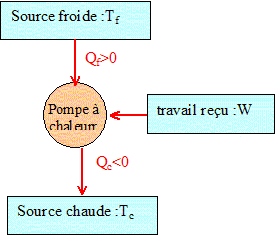
|
|
1.3 On souhaite chauffer l'eau de la piscine de masse m = 54 103 kg à une température de 30°C..
1.3.a. Calculer la variation d'énergie interne de l'eau.
DU = m ceau Dq = 54 103 x 4,18 103 x(30-14)=3,61 109 J.
1.3.b. Déduire le transfert thermique Q2 de la PAC à la source chaude.
Q2 = -3,61 109 J.
1.4 La PAC consomme une puissance életrique Pélec = 25 kW pour une efficacité thermique eth = 3,5.
1.4.a. Calculer l'énergie électrique Welec transférée à la PAC.
eth = énergie utile / énergie fournie = |Q2| / Wélec.
Wélec = 3,61 109 / 3,5 = 1,03 109 J.
La préparation du bateau n"cessite une escale de 12 heures avant la montée des passagers.
1.4.b. Indiquer si la durée de l'escale suffit pour chauffer la piscine.
Wélec / Pélec = 1,03 109 / (2,5 104) =4,13 104 s ou environ 11,5 heures.
La durée de l'escale est suffisante.
1.5. La PAC fonctionnant comme une machine cyclique, son bilan énergétique est nulle sur un cycle.
1.5.a. Montrer que la PAC reçoit de la source froide une énergie E = 2,6 GJ.
3,61 109 -1,03 109 ~2,6 109 J = 2,6 GJ.
1.5.b. Expliquer pourquoi cette énergie peut être qualifiée de gratuite.
L'air extérieur, chauffé par le soleil, est une source d'énergie renouvelable.
Partie II. La patinoire.
Le tapis glacier de la patinoire sera constitué d'une couche d'eau de
largeur l = 8,0 m, de longueur L = 12,0 m et d'épaisseur e = 7,0 cm
environ.
L'eau sera refroidie de 14°C à une température finale de -12°C par un
système de tuyaux dans lesquels circule un fluide réfrigérant.
2.1. Enumérer les différents modes de transferts thermiques, puis expliquer ceux qui sont ici prépondérants.
La conduction et la convection sont prépondérants. Le troisième transfert thermique est le rayonnement.
2.2. Calculer la masse d'eau nécessaire à la fabrication du tapis glacier.
l L e = 8,0 x12,0 x0,070 = 6,72 m3 soit une masse d'eau m= 6,72 tonnes.
2.3 Calculer la variation d'énergie interne de l'eau lors de la fabrication de ce tapis glacier.
Le liquide se refroidit de 14°C à 0°C : mceau Dq = 6,72 103 x4,18 103 (-14)= -3,93 108 J.
Le liquide gèle à 0°C : m Lsolidification = 6,72 103 x(-3,33 105 )= -2,24 109 J.
Le solide se refroidit de 0 à -12 °C : mcglace Dq = 6,72 103 x2,06 103 (-12)= -1,66 108 J.
Variation d'énergie interne de l'eau : -2,8 109 J = -2,8 GJ.
2.4. Indiquer s'il
serait possible de coupler la piscine avec la patinoire sur le plan
énergétique. Expliquer l'intérêt d'un tel couplage.
La PAC pourrait utiliser l'eau du tapis glacier en tant que source
froide à la place de l'air extérieur. La consommation d'énergie
électrique serait minimisée.
La corne de brume ( 7 pts).
La
corne de brume émet un son à proximité des lieux de danger pour se
substituer aux signaux visuels, masqués par le brouillard, afin de
donner l'alerte aux navires. En Bretagne, la chaussée de Sein est une
longue suite d'écueils à fleur d'eau ( environ 7 km).
En 1839 deux phares sont construits, la vieille sur le bec du Raz et
Men Brial sur l'ile de Sein. Par temps clair, leur lumière porte d'un
phare à l'autre, si bien qu'un bateau voyant une lumière par babord et
une lumière par tribord sait qu'il entre dans la zone de danger.
Néanmoins lorsqu'une brume , même légère , obscurçit l'air, la danger
demeure, car la lumière ne porte plus jusqu'à la limite des récifs.
La corne de brume fait partie de la famille des cuivres. C'est la
longueur du tube ( de la corne de brume ) qui détermine la note.
La demi-longueur d'onde de la fréquence du fondamental est égale à la longueur du tube.
La
corne de brume de Daboll avait une longueur proche de 5 m de sorte que
son niveau d'intensité sonore était de 100 dB à 100 m.
Pour une source isotrope de puissance P, l'intensité sonore I en un point M distance de d de la source vaut : I = P / (4pd2).
Objet. Rédiger un rapport apportant une solution technique fiable pour sécuriser la navigation autour de la chaussée de Sein.
Hypothèses de travail :
- L’amortissement de l’onde n’est pas pris en compte : la dissipation d’énergie au cours de la propagation est négligeable.
- Le rayonnement de la source est supposé isotrope.
Installer
sur chaque phare une corne de brume, alimentée par du gaz comprimé, ou
bien installer plusieurs cornes de brume sur des bouées tout le long de
la zone de danger.
Les phares étant distants d'environ 7 km, le son émis par chaque corne
doit posséder un niveau sonore suffisant ( environ 60 dB) à 3,5 km.
Intensité sonore à cette distance : I = I0 x 106 = 10-12 x 106 = 10-6 W m-2.
Puissance de la source : P =4pd2I =4 x3,14 x35002 x10-6 ~ 150 W.
En installant des cornes de brume sur des bouées tous les 500 m, la
puissance de la source serait de ( pour un même niveau
d'intensité sonore ):
P =4pd2I =4 x3,14 x5002 x10-6 ~ 3 W.
La sensibilité de l'oreille est maximale pour une fréquence de 1000 Hz.
A 100 Hz, un son est audible si le niveau d'intensité sonore dépasse 25 dB.
A 30 Hz, un son est audible si le niveau d'intensité sonore dépasse 50 dB.
Dans la région de Brest, pour une température moyenne de 15°C, la célérité du son est d'environ 340 m /s.
Longueur d'onde correspondante a un son de fréquence 100 Hz : l = 340 / 100 = 3,4 m.
Longueur de la corne de brume : 3,4 / 2 = 1,7 m.
|
|