Mathématiques,
concours ENSM 2018
Formation des ingénieurs de l'école normale supérieure maritime
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
3ème question.
On se place dans le plan complexe muni d'un repère orthogonal direct.
On note A le point d'affixe a = 3i, B le point d'affixe b = 2i et C le point d'affixe c = 3 *2½exp(ip/4).
On considère l'application f qui, a tout point M du plan d'affixe z
différent de B, associe le point M' du plan d'affixe z' = 3iz /(z-2i).
1.
Déterminer les affixes des points A' et C', images respectives des
points A et C par f. On donnera ces affixes sous forme algébrique.
a' = (3i)2 /(3i-2i)= -9 /i =9i.
c= 3 *2½(cos p/4) + i sin (p/4))=3 + 3 i=3(1+i).
c'=9i(1+i) / (3+i)= 9i(1+i)(3-i) / 10 =18 /10 (2i-1).
2.. Déterminer, s'il existe, le point D ( d'affixe d) dont l'image par l'application f est le point d'affixe i.
i = 3id /(d-2i) ; (d-2i) i = 3id ; id +2 = 3id ; 2id = 2 ; d = 1/i = -i.
3. Déterminer les affixes des points invariants par f.
zM' = zM ; z =3iz / (z-2i) ; z(z-2i) = 3iz ; z(z-5i) =0 ; z = 0 et z = 5 i.
4. Montrer que, pour tout point M du plan, distinct de B, l'affixe z' de M' vérifie l'égalité :
z'-3i = -6 /(z-2i). (*).
z' -3i= 3iz /(z-2i) -3i =3i ( z / (z-2i) -1) = 3i(2i /(z-2i) = -6 /(z-2i).
5. En déduire que si M appartient au cercle G de centre B et de rayon 3, alors M' appartient à un cercle G' dont vous préciserez le centre et le rayon.
Le point M, d'affixe z = x +iy, appartient au cercle de centre B(0, 2) et de rayon 3.
Equation de ce cercle : x2 +(y-2)2 = 9.
z' -3i= -6 /(x+i(y-2)) =[-6(x-i(y-2)]/ [ x2 +(y-2)2] +3i = -2 / 3 (x+i(2-y)= x' +i(y'-3)
On identifie : x' = -2 / 3 x soit x = -1,5 x ;
y'-3=1 / 3 (2y -4) soit y = 1,5 y' -2,5.
(-1,5x)2 +(1,5 y -2,5-2)2 = 9 ; 1,52 [x2 +(y-3)2 ]= 9 ; x2 +(y-3)2 = 9 / 1,52 = 4.
M' appartient au cercle de centre (0 ; 3) et de rayon 2.
6.
Déduire de l'égalité (*) une mesure de l'angle formé entre l'axe des
abscisses et AM' et une mesure de l'angle formé entre l'axe des
abscisse et BM.
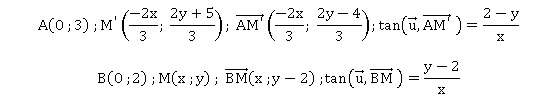
7. Montrer que le point N d'affixe 3 / 2½ +(2 +3 /2½)i est un point de G puis déterminer la mesure de l'angle (u ; BN).
Equation du cercle G : x2 +(y-2)2 =9.
Si N appartient à ce cercle, ces coordonnées vérifient cette équation :
(3 / 2½)2+(3 /2½)2 = 9 / 2 + 9 /2 =9; cette égalité étant vérifiée, N appartient au cercle G.
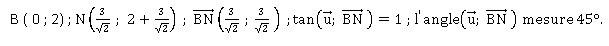
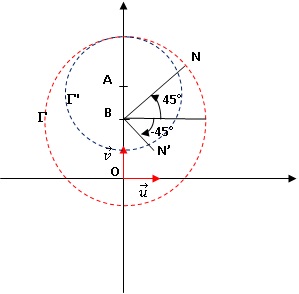
8. En déduire une méthode de construction de N', image de N par l'application f.
|
|
4ème question.
Dans l'espace muni d'un repère orthonormé on considère les points :
A(-4 ; 0 ; 1) , B(3 ; 3 ; -1), C(1 ; 5 ; 1) et D (0 ; 2 ; 6).
1. Justifier que les points A, B et C ne sont pas alignés.
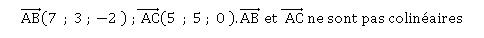
2. Démontrer que le triangle ABC est rectangle en C puis calculer son aire.
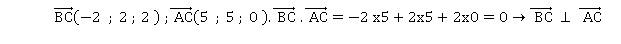
AC= [52+52+02]½=50½ ; BC= [(-2)2+22+22]½=12½ ; AC* BC / 2 = (50 x12)½ /2 =150½ =5*6½.
3. Soit n un vecteur de l'espace de coordonnées (1, b, c) où b et c désignent deux réels.
3.1. Déterminer les valeurs de b et c pour que ce vecteur soit normal au plan (ABC).
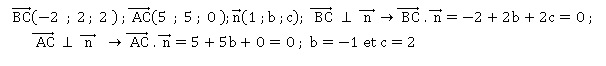
3.2. En déduire une équation cartésienne de ce plan.
x -y+2z +d = 0.
A appartient à ce plan; les coordonnées de A vérifient l'équation du plan.
-4-0+2+d=0 soit d = 2.
x -y+2z +2 = 0.
3.3. Le point D appartient-il au plan (ABC) ?
Si D(0 ; 2 ; 6) appartient à ce plan; ces coordonnées doivent vérifier l'équation du plan.
0-2+2x6+2 = 12, différent de zéro.
D n'appartient pas au plan (ABC).
4.Soit (d) la droite orthogonale à (ABC) passant par D.
4.1. Donner une représentation paramétrique de (d).
Le vecteur n(1 ; -1 ; 2) est un vecteur directeur de cette droite.
x = t+a ; y = -t +e ; z = 2t+f.
Cette droite passe par D :
x = t ; y = -t+2 ; z=2t +6 avec t réel.
4.2 Déterminer les coordonnées du point d'intersection H de d avec (ABC).
Les coordonnées de H vérifient à la fois les équations paramétriques de d et l'équation du plan.
t-(-t+2)+2(2t+6)+2=0.
6t +12 = 0 ; t = -2.
H( -2 ; 4 ; 2 ).
|
|
5.1 Calculer la distance DH. Donner la valeur exacte.
DH =[(-2-0)2 +(4-2)2+(2-6)2]½ =24½ = 2*6½.
5.2. En déduire le volume du tétraèdre ABCD. Donner la valeur exacte.
aire de la base ABC fois hauteur DH / 3 =5*6½*2*6½ / 3 = 20.
6. Calculer une mesure de l'angle ADB arrondie au degré près.
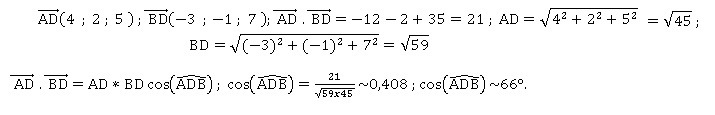
|
|