Mathématiques,
concours ENSM 2018
Formation des ingénieurs de l'école normale supérieure maritime
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
2ème question.
1. Etude d'une fonction.
On considère la fonction f définie sur [0 ; +oo[ par f(x) = 5-4 / (x+1).
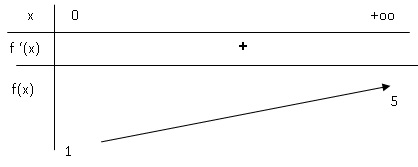
1.1. Dresser le tableau de variation complet sur son ensemble de définition.
Limites : quand x tend vers l'infini, f(x) tend vers 5.
Quand x tend vers zéro, f(x) tend vers 1.
Dérivée : f '(x) = 4 /(x+1)2. f '(x) est positive et f(x) est strictement croissante sur [0 ; +oo[
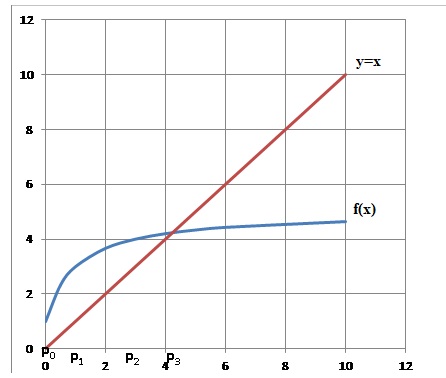
1.2. Résoudre l'équation f(x) = x et montrer qu'elle admet une solution unique a dont on donnera la valeur exacte et un arrondi à 10-2 près.
5-4 /(x+1) = x ; 5(x+1) -4-x(x+1) =0 ; -x2 +4x+1 = 0.
Discriminant D = 42 +4 = 20 ; on retient la solution positive : a = (-4 -2*5½) /(-2) = 2+5½~4,23.
1.3. Démontrer que pour tout x appartenant à [0 ; a], f(x) appartient à [0 ; a].
f(0) = 1 ; f(a) = (5a-1) / (1+a) ~3,85, inférieur à a.
f(x) est strictement croissante sur [0 ; a]. D'après le théorème des valeurs intermédiaires, pour tout x appartenant à [0 ; a], f(x) appartient à [0 ; a].
2. Etude d'une suite.
On considère la suite (un) définie par u0 = 0 et pour tout entier naturel n par un+1 = f(un).
2.1. Calculer u1.
u1=f(u0) = 1 ; u2 = f(1) =3 ; u3 =4 ; u4=4,2.
2.2. Construire graphiquement sur l'axe des abscisses les points P0, P1, P2, P3 d'abscisses respectives u0, u1, u2 et u3.
|
|
2.3 Quelles conjectures peut-on faire sur le sens de variation et la convergence de (un) ?
La suite est croissante et bornée. Donc elle converge.
2.4. Démontrer par récurrence que pour tout entier naturel n, 0 < un < un+1 < a.
Initialisation : 0 < u0 < u1 < a. La propriété est vraie au rang zéro.
Hérédité : on suppose que 0 < up < up+1 < a est vraie.
f(x) étant strictement croissante sur [0 ; a] et f(x) appartenant à [0 ; a].
0 < f(up) < f(up+1) < a , donc 0 < up+1 < up+2 < a est vraie.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel.
2.5. En déduire que (un) est convergente et calculer sa limite.
f(x) étant strictement croissante sur [0 ; a] et f(x) appartenant à [0 ; a] :
la suite est strictement croissante et bornée par a, donc elle converge.
2.6. Ecrire en langage naturel un algorithme qui demande la valeur de e et affiche en sortie le premier entier n tel que |un-a| < e.
Variables : n entier ; un, e , a réels.
un = u0=0.
n=0.
Affecter à a la valeur de a.
Demander la valeur de e et affecter cette valeur à e.
Tant que |un-a| < e faire :
Affecter à un la valeur 5-4 / (un+1).
n = n+1.
Fin Tant que
Afficher n.
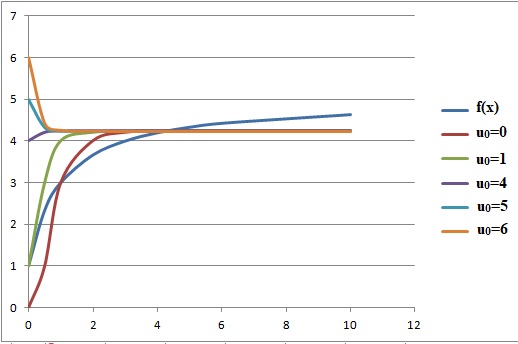
3. On donne à u0 une valeur positive quelconque.
Emettre une conjecture sur le sens de variation et la limite de la suite (un) en fonction des valeurs de u0.
un+1 = f(un) et la fonction f est strictement croissante sur [0 ; +oo[.
De plus 1 < f(x) < 5.
0 < u0 < a, la suite est strictement croissante et bornée par a.
u0 = a, la suite est constante.
a < u0 , la suite est strictement décroissante et bornée par a.
|
|