Mathématiques,
Brevet Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
.
.
|
|
Exercice
1.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1. Scratch souhaite
rejoindre un ami, mais il a oublié la fin du trajet. Il décide de finir
son trajet en prenant, aux intersections, à droite ou à gauche au
hasard.
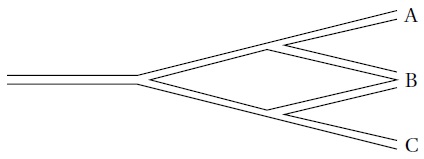
Affirmation 1 : La probabilité qu’il arrive en A, en B ou en C est la même. Faux.
La probabilité d'arriver en B est deux fois plus grande que celle d'arriver en A ou en C.
2.
On suppose qu’une éolienne produit 5 GWh d’électricité par an et qu’une
personne a besoin de 7 000 kWh d’électricité par an. (Wh :Watt-heure)
Affirmation 2 : Une éolienne ne couvre pas les besoins en électricité de 1 000 personnes pour un an. Vrai.
7000 kWh = 7 MWh ; 7 x1000 = 7000 MWh = 7 GWh, valeur supérieure à 5.
3. Voici quatre nombres : 45% ; 305 / 612 ; 0,5 ; 730×10−3.
Affirmation 3 : Ces quatre nombres sont rangés dans l’ordre croissant. Vrai.
45 % = 0,45 ; 305 / 602 ~0,507 ; 730×10−3 = 0,73.
4. L’histogramme ci-dessous représente la répartition des salaires dans une entreprise :
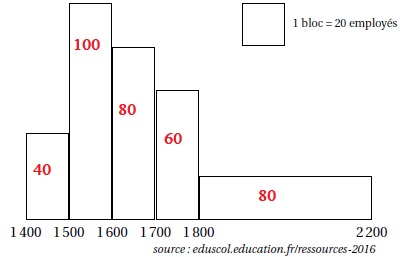
Affirmation 4 : Plus de 40% des employés ont un salaire au moins égal à 1 700 €. Faux.
Nombre d'employés gagnant plus de 1700 € : 140.
Nombre total d'employés : 360.
140 / 360 ~0,39 ( 39 %).
Exercice 2 .
Les
baleines émettent des sons, de fréquences comprises entre 10 Hz et 10
kHz, qui se propagent dans l’eau à une vitesse d’environ 1 500 m/s.
L’étude des chants des baleines a pour but d’élucider leur possible
signification; sélection du partenaire sexuel et communication sociale
sont des hypothèses envisagées.
1. Convertir la vitesse de propagation de ces sons en km/h.
1500 x3,6 = 5400 km /h.
2. Deux groupes de baleines situées au large de l’Alaska communiquent entre eux.
a. Calculer la distance séparant les deux groupes de baleines. Vous donnerez le résultat arrondi à 50 km près.
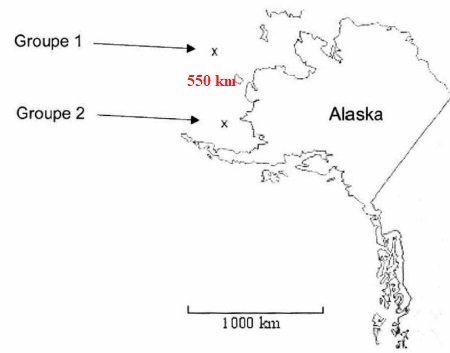
b. Combien de temps met une onde sonore émise par une baleine du groupe 1 pour parvenir aux baleines du groupe 2 ?
Vous donnerez le résultat arrondi à la minute.
550 / 5400 ~0,102 heure ou environ 6 minutes.
3. Le dessin ci-dessous donne une idée de la taille d’une baleine bleue par rapport à celle d’un homme.
En considérant que le plongeur sur l’image a une taille égale à 1,75 m,
calculer la taille approximative de la baleine représentée ci-dessous.
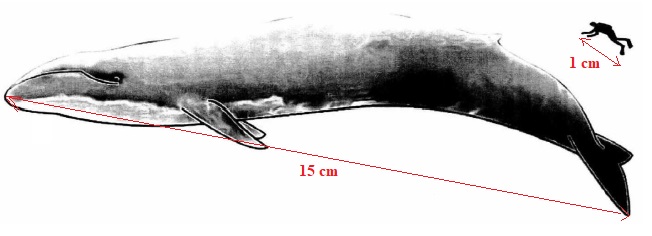
1,75 x15 ~ 26 m.
Exercice 3.
On
demande à quinze élèves d’une classe A et à dix élèves d’une classe B
de compter le nombre de SMS qu’ils envoient pendant un week-end.
Le lundi on récupère les résultats dans un tableur.

1. Calculer le nombre moyen et le nombre médian de SMS envoyés pendant le week-end par ces élèves de la classe A.
Moyenne :(5 +7 +12 +15 +15 +16 +18 +21 +34 +67) / 15 = 14.
Médiane : il y a 15 données rangées par ordre croissant : la médiane correspond à un nombre compris entre 7 et 12.
2. Quelles formules ont pu être écrites dans les cellules Q3 et R3 du tableur ?
=MOYENNE(B2:P2) ou = SOMME(B2:P2)/15
=(F3+G3)/2
3. Calculer le nombre moyen de SMS envoyés pendant le week-end par ces 25 élèves des classes A et B.
(12 x10 + 14 x15) / 25 = 13,2.
4. Calculer le nombremédian de SMS envoyés pendant le week-end par ces 25 élèves des classes A et B.
Ranger les nombres par ordre croissant et prendre la valeur du 13è nombre soit 12.
|
|
Exercice
4.
1.
Le responsable du plus grand club omnisport de la région a constaté
qu’entre le 1er janvier 2010 et le 31 décembre 2012 le nombre total de
ses adhérents a augmenté de 10% puis celui-ci a de nouveau augmenté de
5% entre le 1er janvier 2013 et le 31 décembre 2015.
Le nombre total d’adhérents en 2010 était de 1 000.
a. Calculer, en justifiant, le nombre total d’adhérents au 31 décembre 2012.
1000 x1,1 = 1100.
b. Calculer, en justifiant, le nombre total d’adhérents au 31 décembre 2015.
1100 x1,05 = 1155.
c. Martine pense qu’au 31 décembre 2015, il devrait y avoir 1 150 adhérents car elle affirme :
« une augmentation de 10% puis une autre de 5%, cela fait une augmentation de 15%».
Qu’en pensez-vous ? Expliquez votre réponse.
1,1 x1,05 = 1,155 soit une augmentation de 15,5 %.
2. Au 1er janvier 2017, les effectifs étaient de 1 260 adhérents.
Voici le tableau de répartition des adhérents en 2017 en fonction de leur sport de prédilection.
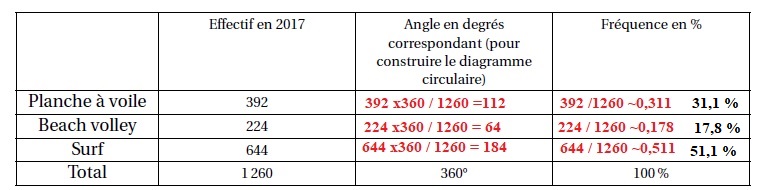
a. Compléter, la colonne intitulée « Angle en degrés correspondant ».
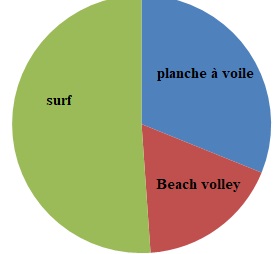
b. Pour représenter la situation, construire un diagramme circulaire de rayon 4 cm.
c. Compléter la colonne « Fréquence en % ».
Exercice 5.
Les deux parties de cet exercice sont indépendantes.
Mario, qui dirige un centre de plongée sous-marine en pleine expansion,
décide de construire un bâtiment pour accueillir ses clients lors de la
pause déjeuner. Celui-ci sera constitué d’un rez-dechaussée climatisé
servant de réfectoire et d’un étage non climatisé qui pourra être
utilisé pour le
stockage du matériel de plongée.
Pour finir d’établir son budget, il ne lui reste plus qu’à choisir un
modèle de climatisation adapté et à calculer la quantité nécessaire de
tuiles pour couvrir le toit de sa construction qu’il a schématisé
ci-dessous.
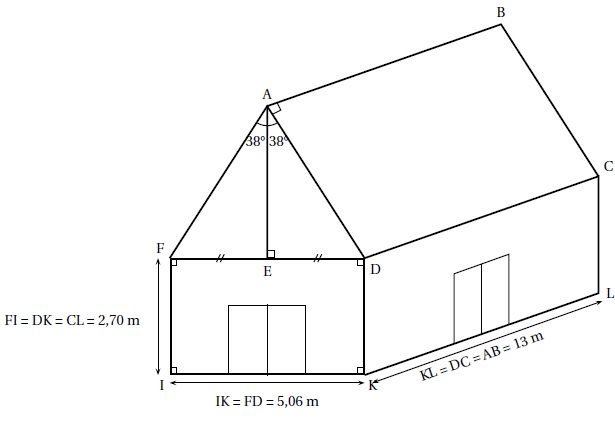
1. PARTIE 1 : Calcul du budget correspondant aux tuiles.
a. Calculer AD. Vous donnerez le résultat arrondi au centimètre près.
Dans le triangle rectangle ADE : sin 38 = ED/ AD = 2,53 / AD.
AD = 2,53 / sin 38 ~4,11 m.
b. Calculer AE. Vous donnerez le résultat arrondi au centimètre près.
Dans le triangle rectangle ADE : tan 38 = ED/ AE = 2,53 / AE.
AE = 2,53 / tan 38 ~3,24 m.
c. En déduire le prix des tuiles nécessaires à la couverture des deux pentes du toit.
Prévoir 26 tuiles par m2
Prix : 0,65 euro l’unité.
Surface des deux pans : 2 x13 x4,11=106,86 m2.
Prix des tuiles : 106,86 x26 x0,65 ~1806 €.
2. PARTIE 2 : Choix d’un climatiseur adapté.
À l’aide des documents, faire un choix de climatiseur raisonné, adapté et le moins cher possible
pour climatiser le rez-de-chaussée du bâtiment, c’est dire à dire le réfectoire.
Volume de la pièce à refroidir : 13 x2,7 x5,06 =177,6 m3.
La puissance frigorifique sera comprise entre 18 000 BTU et 25 000 BTU.
On peut choisir le Freez 8000 à 1050 € ou le Air 10 pingouin à 990 €.
|
|
Exercice 6.
Voici un script saisi par Alice dans un logiciel d’algorithmique.
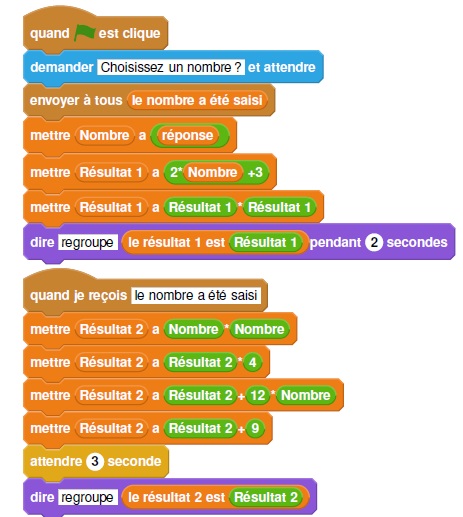
1. Alice a choisi 3 comme nombre, calculer les valeurs de Résultat 1 et de Résultat 2 ?
Justifier en faisant apparaître les calculs réalisés.
Résultat 1 = (2 x3 +3)2=(6+3)2 = 81.
Résultat 2 = 32 x4 +12 x3 +9 = 81.
2. Généralisation
a. En appelant x le
nombre choisi dans l’algorithme, donner une expression littérale
traduisant la première partie de l’algorithme correspondant à Résultat
1.
Résultat 1 = (2 x +3)2.
b.
En appelant x le nombre choisi dans l’algorithme, donner une expression
littérale traduisant la deuxième partie de l’algorithme correspondant à
Résultat 2.
Résultat 2 = 4x2 +12 x +9.
c. Trouver le ou les nombres choisis par Alice qui correspondent à Résultat 2 = 9.
4x2 +12 x +9= 9.
4x2 +12 x =0 ;
4x(x+3) =0.
x = 0 et x = -3.
|
|