Mathématiques, Brevet Métropole 2018

Mathématiques, Brevet Métropole 2018 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
	. .
	. .
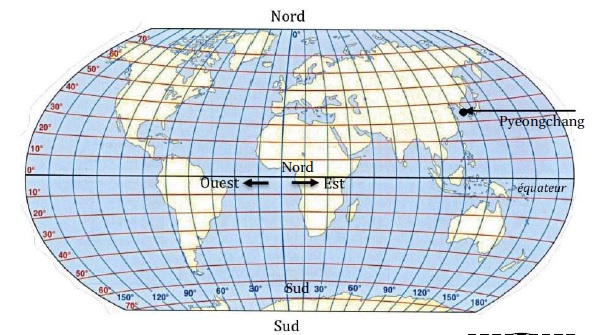
	Exercice 1. Le gros globe de cristal est un trophée attribué au vainqueur de la coupe du monde de ski. Ce trophée pèse 9 kg et mesure 46 cm de hauteur. 1. Le biathlète français Martin Fourcade a remporté le sixième gros globe de cristal de sa carrière en 2017 à Pyeongchang en Corée du Sud. Donner approximativement la latitude et la longitude de ce lieu repéré sur la carte ci-dessous. Longitude : 130° Est ; latitude :35° Nord. 2. On considère que ce globe est composé d’un cylindre en cristal de diamètre 6 cm, surmonté d’une boule de cristal. Montrer qu’une valeur approchée du volume de la boule de ce trophée est de 6 371 cm³. 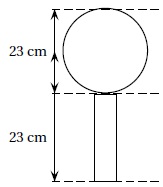V = 4 / 3 p R³ avec R = 11,5 cm. V = 4 / 3 x3,14 x11,5³ ~ 6 371 cm³. 3. Marie affirme que le volume de la boule de cristal représente environ 90% du volume total du trophée. A-t-elle raison ? Volume du cylindre : pr²h avec r = 3 cm. 3,14 x 3² x23 ~ 650 cm³. Volume total : 6371 +650 = 7021 cm³. La boule représennte 6371 / 7021 ~0,907 ( 90,7 %) du volume total. Elle a raison. Exercice 2 . Parmi les nombreux polluants de l’air, les particules fines sont régulièrement surveillées. Les PM10 sont des particules fines dont le diamètre est inférieur à 0,01 mm. En janvier 2017, les villes de Lyon et Grenoble ont connu un épisode de pollution aux particules fines. 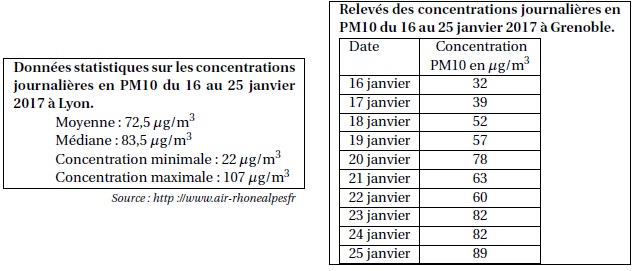Voici des données concernant la période du 16 au 25 janvier 2017 : 1. Laquelle de ces deux villes a eu la plus forte concentration moyenne en PM10 entre le 16 et le 25 janvier ? A Grenoble, la moyenne est égale à : (32 +39 +52 +57 +78 +63 +60 +82 +82 +89) / 10 = 63,4 µg m^-3. La ville de Lyon a eu la plus forte concentration en particules PM10. 2. Calculer l’étendue des séries des relevés en PM10 à Lyon et à Grenoble. Laquelle de ces deux villes a eu l’étendue la plus importante ? Interpréter ce dernier résultat. Lyon : 107-22 = 85 µg m^-3. Grenoble : 89-32 = 57 µg m^-3. La ville de Lyon a eu l’étendue la plus importante. 3. L’affirmation suivante est-elle exacte? Justifier votre réponse. « Du 16 au 25 janvier, le seuil d’alerte de 80 μg/m³ par jour a été dépassé au moins 5 fois à Lyon ». La médiane est égale à 83,5 μg/m³. La série possède 10 valeurs ; 5 valeurs sont supérieures à 83,5 μg/m³. l'affirmation est exacte. Exercice 3. Dans son lecteur audio, Théo a téléchargé 375 morceaux de musique. Parmi eux, il y a 125 morceaux de rap. Il appuie sur la touche « lecture aléatoire » qui lui permet d’écouter un morceau choisi au hasard parmi tous les morceaux disponibles. 1. Quelle est la probabilité qu’il écoute du ? 125 / 375 = 1 / 3 ~0,33. _2.La probabilité qu’il écoute du rock est égale à 7 / 15 . Combien Théo a-t-il de morceaux de rock dans son lecteur audio ? 7 / 15 x375 = 175. 3. Alice possède 40% de morceaux de rock dans son lecteur audio. Si Théo et Alice appuient tous les deux sur la touche « lecture aléatoire » de leur lecteur audio, lequel a le plus de chances d’écouter un morceau de rock ? Théo : 7 / 15 ~0,467 ( 46,7 %), valeur supérieure à 40 %. Théo a le plus de chances d’écouter un morceau de rock.
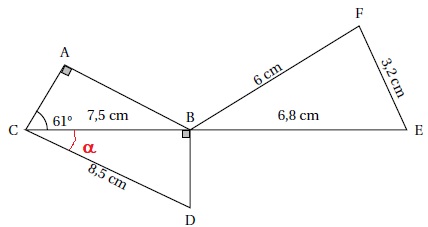
	Exercice 4. La figure ci-dessous n’est pas représentée en vraie grandeur. Les points C, B et E sont alignés. Le triangle ABC est rectangle en A. Le triangle BDC est rectangle en B. 1. Montrer que la longueur BD est égale à 4 cm. Dans le triangle rectangle BDC : CD² = BC²+BD² ; BD² =8,5² -7,5² = 16 ; BD = 4 cm. 2. Montrer que les triangles CBD et BFE sont semblables. Les mesures des cotés de deux triangles semblables sont proportionnelles. BD / FE = 4 / 3,2 = 1,25. BC / BF = 7,5 / 6=1,25. CD / BE = 8,5 / 6,8 = 1,25. Les triangles CBD et BFE sont semblables. 3. Sophie affirme que l’angle BFE est un angle droit. A-t-elle raison ? Les triangles CBD et BFE sont semblables et le triangle CBD est rectangle en B. Donc le triangle BFE est rectangle en F. Elle a raison. 4. Max affirme que l’angle �ACD est un angle droit. A-t-il raison? tan a = BD / BC = 4 / 7,5 ~0,533 ; a ~28 °. 61 + 28 = 89°, valeur différente de 90°. L’angle �ACD n'est pas un angle droit. Exercice 5. Voici un programme de calcul • Choisir un nombre • Multiplier ce nombre par 4 • Ajouter 8 • Multiplier le résultat par 2 1. Vérifier que si on choisit le nombre −1, ce programme donne 8 comme résultat final. (-1 x4 +8) x2= (-4+8)x2 = 4 x2 = 8. 2. Le programme donne 30 comme résultat final, quel est le nombre choisi au départ ? Soit x le nombre choisi : (4x+8)*2=30. 4x+8 = 15 ; 4x = 15-8 = 7 ; x = 7 /4 = 1,75 Dans la suite de l’exercice, on nomme x le nombre choisi au départ. 3. L’expression A = 2(4x+8) donne le résultat du programme de calcul précédent pour un nombre x donné. On pose B = (4+x)² −x². Prouver que les expressions A et B sont égales pour toutes les valeurs de x. B = (4+x-x)(4+x+x) = 4(4+2x) = 2(8+4x)= A. 4. Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées. • Affirmation 1 : Ce programme donne un résultat positif pour toutes les valeurs de x. Faux. Le résultat a le signe de 8 +4x. 8 +4x >0 si x > - 2 ; 8 +4x < 0 si x < -2. • Affirmation 2 : Si le nombre x choisi est un nombre entier, le résultat obtenu est un multiple de 8. Vrai. A = 8(2+x). si x est entier, A est un multiple de 8.
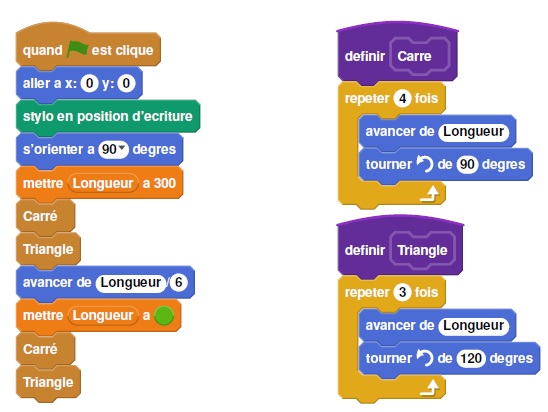
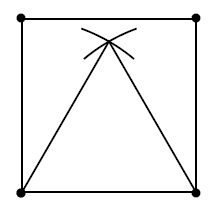
	Exercice 6. Les longueurs sont en pixels. L’expression « s’orienter à 90 » signifie que l’on s’oriente vers la droite. On donne le programme suivant : 1. On prend comme échelle 1 cm pour 50 pixels. a. Représenter sur votre copie la figure obtenue si le programme est exécuté jusqu’à la ligne 7 comprise. b. Quelles sont les coordonnées du stylo après l’exécution de la ligne 8 ? x = 300 / 6 = 50 ; y = 0. 2. On exécute le programme complet et on obtient la figure ci-dessous qui possède un axe de symétrie vertical. 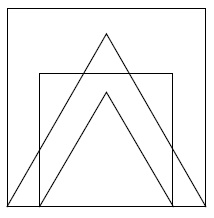Recopier et compléter la ligne 9 du programme pour obtenir cette figure. Mettre longueur à 200. 3. a. Parmi les transformations suivantes, translation, homothétie, rotation, symétrie axiale, quelle est la transformation géométrique qui permet d’obtenir le petit carré à partir du grand carré? Préciser le rapport de réduction. Homothétie de rapport 2 /3. b. Quel est le rapport des aires entre les deux carrés dessinés ? (2 /3)² = 4 / 9. Exercice 7. Le « hand-spinner » est une sorte de toupie plate qui tourne sur elle-même. On donne au « hand-spinner » une vitesse de rotation initiale au temps t = 0, puis, au cours du temps, sa vitesse de rotation diminue jusqu’à l’arrêt complet du « hand-spinner ». Sa vitesse de rotation est alors égale à 0. Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde. 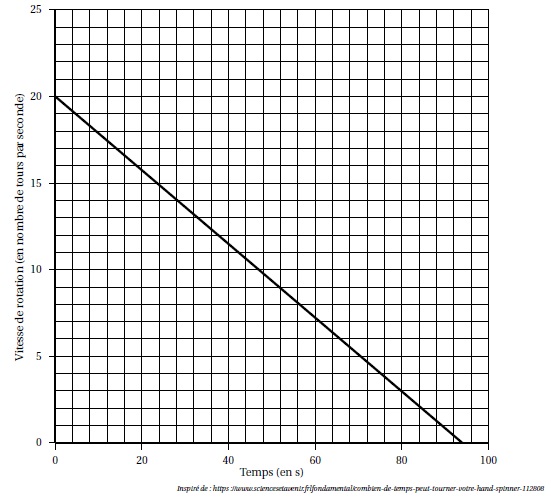Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde : 1. Le temps et la vitesse de rotation du « hand-spinner » sont-ils proportionnels ? Justifier. Non, la droite ne passe pas par l'origine. 2. Par lecture graphique, répondre aux questions suivantes : a. Quelle est la vitesse de rotation initiale du « hand-spinner » (en nombre de tours par seconde) ? 20 tours / seconde. b. Quelle est la vitesse de rotation du « hand-spinner » (en nombre de tours par seconde) au bout d’une minute et vingt secondes ? 3 tours / seconde. c. Au bout de combien de temps, le « hand-spinner » va-t-il s’arrêter ? 93 secondes. 3. Pour calculer la vitesse de rotation du « hand-spinner » en fonction du temps t , notée V (t ), on utilise la fonction suivante : V (t ) = −0,214×t +V_initiale. • t est le temps (exprimé en s) qui s’est écoulé depuis le début de rotation du « hand-spinner » ; • Vinitiale est la vitesse de rotation à laquelle on a lancé le « hand-spinner » au départ. a. On lance le « hand-spinner » à une vitesse initiale de 20 tours par seconde. Sa vitesse de rotation est donc donnée par la formule : V (t ) = −0,214×t +20. Calculer sa vitesse de rotation au bout de 30 s. V(30) = -0,214 x30 +20 = 13,58 tours / seconde. b. Au bout de combien de temps le hand-spinner va-t-il s’arrêter ? Justifier par un calcul. 0 = -0,214 y +20 ; 0,214 t = 20 ; t = 20 / 0,214 ~93,5 s. c. Est-il vrai que, d’une manière générale, si l’on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps ? Justifier. t = V_initiale/ 0,214. Si la vitesse initiale double, la durée de la rotation double. C'est donc vrai.