Physique
chimie, l'avion Solar impulse 2 a traversé l'Atlantique,
Bac STI2D STL Métropole 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Partie 1 - Les panneaux solaires de Solar Impulse 2 sont-ils performants ?
Solar Impulse 2 est presque entièrement recouvert de panneaux solaires photovoltaïques.
Les matériaux semi-conducteurs utilisés pour constituer les cellules photovoltaïques sont le résultat de nombreuses recherches.
1.1 Déterminer la longueur d’onde des photons pour lesquels la réponse spectrale du semi-conducteur est maximale.
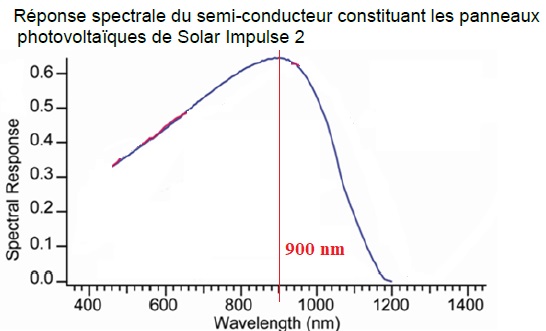
1.2 À quel domaine des ondes lumineuses ces photons appartiennent-ils ? Justifier.
900 nm étant supérieur à 800 nm ( limite du visible et de l'IR ), ces photons appartiennent au proche infrarouge.
1.3 Indiquer si ces photons sont ionisants.
Energie de ces photons : E = h c / l = 6,62 10-34 x3,00 108 / (900 10-9) =2,2 10-19 J ou 2,2 10-19 /(1,6 10-19) ~ 1,4 eV
Les photons du proche IR ne sont pas ionisants.
1.4 Expliquer pourquoi ce type de matériau présente un intérêt dans le fonctionnement des cellules photovoltaïques ?
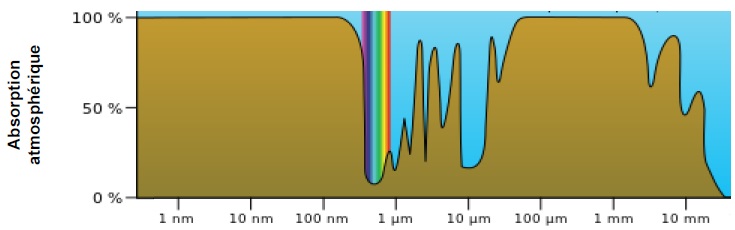
L'atmosphère absorbe très peu les photons de longueur d'onde 0,9 µm.
1.5 Pendant les 14
heures de vol de jour, la puissance surfacique moyenne du rayonnement
solaire réellement disponible est de 450 W·m−2. Calculer dans ces conditions l’énergie solaire en kWh reçue par l’ensemble des panneaux pendant cette durée.
Surface des panneaux :S = 270 m2.
Puissance reçue : 270 x450 = 1,215 105 W.
Energie solaire reçue : 1,215 105 x 14 =1,7 106 Wh = 1,7 103 kWh..
1.6 Les mesures
effectuées ont permis de montrer que l’énergie électrique disponible à
la sortie des panneaux solaires était de l’ordre de 370 kWh par jour.
En déduire le rendement des panneaux solaires utilisés pour Solar
Impulse 2.
Rendement = énergie électrique disponible / énergie solaire reçue = 370 / 1700 ~0,22 ( 22 %).
1.7 Les propos
annoncés par la firme américaine Sun Power dans le document 1.6
sont-ils justifiés ? Argumenter votre réponse en vous appuyant sur les
documents à votre disposition et les résultats obtenus.
Le rendement maximum des panneaux en silicium monocristallin est de 25 % en laboratoire. Les propos sont donc justifiés.
|
|
|
|
|
Partie 2 - Comment justifier le choix de batteries lithium-ion-polymère ?
Pour assurer le vol de nuit, Solar impulse 2 est équipé de batteries au lithium-ion-polymère.
Le fonctionnement de l’avion est étudié pour un vol en palier stabilisé à 8500 m d’altitude à une vitesse constante.
2.1 Exprimer et calculer en kWh l’énergie EBatt nécessaire
pour effectuer un vol de nuit de 10 heures en supposant que la
puissance électrique nécessaire à la traction de l’avion est de 6,0 kW.
60, x 10 = 60 kWh.
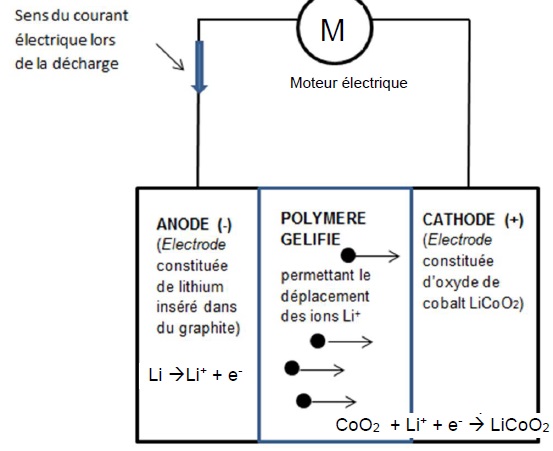
2.2 Quel est l’oxydant du couple oxydant-réducteur mis en jeu à l’anode ? S’agit-il d’une oxydation ou d’une réduction ? Justifier.
A l'anode le réducteur Li cède des électrons. Il s'agit d'une oxydation.
2.3 Montrer que la quantité d’électricité fournie par les batteries vaut Q = 7,2·105 C.
On suppose que la tension aux bornes des batteries vaut U = 300 V.
60 kWh = 60 x3600 kJ = .2,16 105 kJ = 2,16 108 J.
Q = énergie (J) / tension (V)=2,16 108 / 300 = 7,2·105 C.
2.4 Calculer, en mol, la quantité d’électrons échangés dans ces conditions ?
Donnée : la charge électrique d’1 mole d’électrons est de 96 500 C.
Q / 96500 = 7,2 105 / 96500 = 7,46 mol.
2.5 Montrer que la masse de lithium consommée pendant une nuit de 10 heures est proche de mNuit(Li) = 52 g.
Donnée : la masse molaire du lithium est M(Li) = 6,9 g·mol-1.
6,9 x7,46 = 51,5 ~52 g.
2.6 La masse
maximale de lithium oxydable disponible lors de la décharge totale des
batteries de Solar impulse 2 est m(Li) = 142 g. Retrouver, par le
calcul, la valeur de l’énergie totale disponible avec les batteries
décrites dans le document 2.2.( 164 kWh).
52 g de lithium correspond à 60 kWh ; 142 g correspond à : 60 / 52 x 142 ~164 kWh.
2.7 En déduire la densité énergétique massique des batteries au lithium-ion-polymère en kWh·kg-1.
Masse totale des batterie : 660 kg.
164 / 660 ~0,248 kWh kg-1=248 Wh / kg.
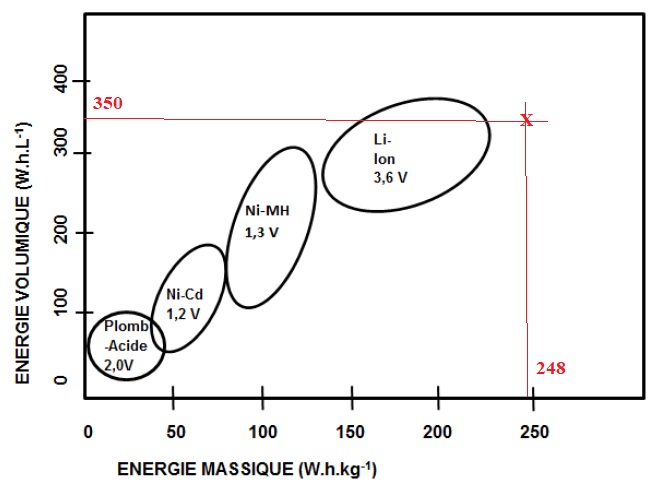
2.8 Indiquer à
l’aide d’une croix la position des batteries d'accumulateurs
lithium-ion-polymère utilisées pour Solar Impulse. Quels sont les
avantages de ces batteries ? Energie volumique des batteries Li ion :
350 Wh / L.
|
|
Partie 3 - Analyse du plan de vol de Solar Impulse.
Un avion motorisé est soumis à trois types d’actions mécaniques lors d’un vol en palier stabilisé :
- la poussée du réacteur ou la traction T de l'hélice entraînée par le moteur ;
- le poids P , effet de la gravité terrestre sur la masse de l'appareil ;
- la résultante des forces aérodynamiques décomposée en portance et en traînée :
* la portance L créée par le déplacement dans l'air d'une aile profilée, est opposée au poids.
* la traînée D, somme des résistances aérodynamiques, est opposée au mouvement.
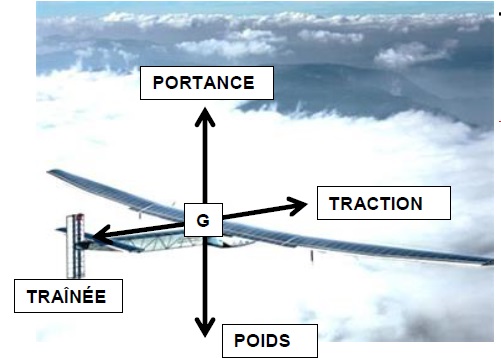
3.1 En vol
horizontal stabilisé, l’avion a un mouvement rectiligne et uniforme.
Justifier le fait que les intensités de la force de traction T et de la
force de trainée D sont égales.
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces
appliquées à l'avion est nulle ( principe d'inertie ou première loi de
Newton ).
3.2 En effectuant une analyse dimensionnelle, montrer que le coefficient de traînée Cx intervenant dans l’expression littérale de l’intensité de la traînée n’a pas d’unité.
T = ½ S Cx r V2.
T : N soit kg m s-2.
S m2 ; r : kg m-3 ; V m s-1.
S r V2 s'exprime en m2 kg m-3 m2 s-2 soit : kg m s-2.
3.3 Compte tenu de l’expression de l’intensité de la trainée, montrer que la puissance PM développée en vol stabilisé à vitesse constante par les moteurs peut s’écrire sous la forme : PM =½ S Cx r V3.
Le mouvement étant rectiligne uniforme : Traction = trainée = ½ S Cx r V2.
La puissance PM est égale à l'intensité de le force fois la norme de la vitesse.
3.4 En supposant que la vitesse de l’avion est maintenue constante, comment varie cette puissance en fonction de l’altitude ?
La masse volumique de l'air diminue avec l'altitude. PM est proportionnelle à la masse volumique de l'air. PM diminue avec l'altitude.
3.5 Calculer la valeur de la puissance développée par les moteurs à 2000 mètres d’altitude pour une vitesse de 45 km·h-1 et un coefficient Cx = 0,012. On admettra que la surface S de l’avion soumise à la force de traînée est de 197 m2.
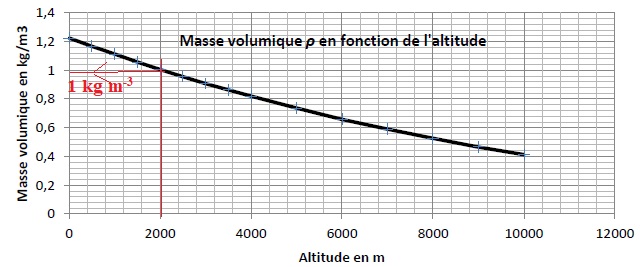
V = 45 / 3,6 = 12,5 m /s.
PM =0,5 x197 x0,012 x1 x 12,53=2,3 103 W
3.6 Quels arguments énergétiques peut-on évoquer pour expliquer les différentes étapes du plan de vol de l’avion sur 24 heures ?
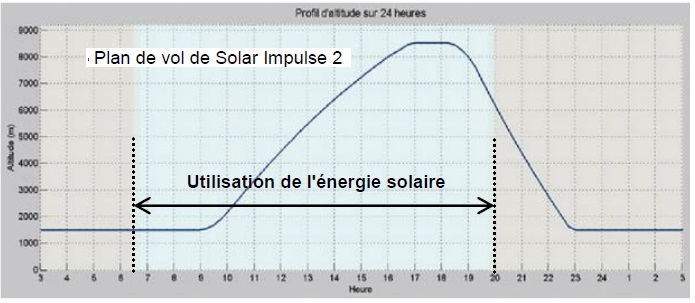
Entre 23 h et 6 h 30, les batteries sont utilisées afin que les moteurs permettent de maintenir une altitude constante.
Entre 6 h 30 et 18 h 30, l'énergie solaire permet de recharger la
batteries et de faire fonctionner les moteurs. L'avion prende de
l'altitude et stocke de l'énergie potentielle de pesanteur et de
l'énergie chimique dans les batteries..
De 18 h 30 à 23 h, moteurs éteints, l'avion plane et restitue
l'énergie potentielle de pesanteu lors de sa descente.
|
|