Physique
chimie, la formule 1 à la pointe de la technologie,
Bac STI2D STL Nlle Calédonie 03 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Partie A. La formule 1 hybride.
A1. Le moteur à combustion.
On suppose que le carburant utilisé est constitué d'iso-octane.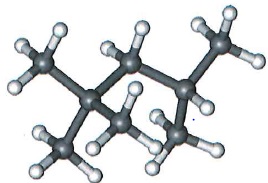 A.1.1. Donner la formule brute de l'iso-octane.
A.1.1. Donner la formule brute de l'iso-octane.
C8H18.
A.1.2. Ecriire l'équation de la réaction de combustion de l'iso-octane.
C8H18 + 12,5 O2 ---> 8 CO2 + 9H2O.
A.1.3. Calculer la
masse molaire de l'iso-octane et montrer que la quantité de matière
d'iso-octane maximale consommée dans le réservoir d"une formule 1
pendant une course vaut n = 877 mol.
Les moteurs ne peuvent pas consommer plus de 100 kg de carburant par voiture et par course, le ravitaillement étant interdit.
M = 8 x 12 +18 = 114 g / mol.
n = 100 103 / 114 ~ 877 mol.
A.1.4. Calculer la quantité de matière de dioxyde de carbone maximale libérée pendanr une course.
8 x 877 =7016 ~7,02 103 mol.
A.1.5. Calculer la masse correspondante de dioxyde de carbone. M(CO2) = 44 g / mol.
m = 44 x 7016 = 3,09 105 g = 309 kg.
A.1.6. La course doit faire au
minimum 305 km. Montrer que la classe énergétique d'un formule 1
correspond au niveau G si on retient la distance minimale.
3,09 105 / 305 ~1,01 103 g de CO2 par km.
Cette valeur étant supérieure à 250, le niveau est G.
A.1.7. Calculer, en litres, le volume maximal, VR, d'iso-octane consommé par une Formule 1 lors d'une course.
Masse volumique du carburant r = 714 kg m-3.
100 / 714 = 0,140 m3 = 140 L.
A.1.8. Lors d'une
course de Formule 1, la consommation moyenne en essence est de 56 L aux
100 km. Montrer qu'une Formule 1 n'a pas assez d'énergie chimique pour
finir une course.
56 x305 / 100 ~171 L, valeur supérieure à 140 L.
A.2. Récupération de l'énergie
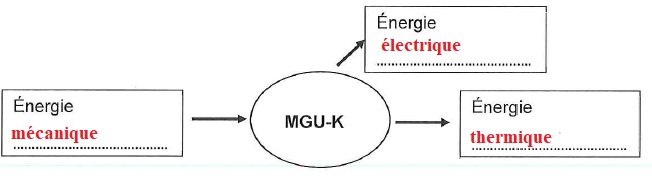
A.2.1 Compléter le
document réponse DR1 de la page 18, en précisant la nature des énergies
mises en jeu par le MGU-K lors d'une phase de freinage.
L'ènergie
mécanique est en partie dissipée par les freins sous forme de chaleur
et en partie convertie en énergie électrique stockée dans
la batterie.
A.2.2 La puissance
maximale du MGU-K est de 120 kW et la quantité d'énergie maximale
autorisée à être stockée est de 2,00 MJ à chaque tour de circuit.
Calculer la durée minimale, en secondes (s), de freinage, Δtf, par tour dont a besoin la Formule 1 pour atteindre cette charge maximale.
2000 MJ = 2,00 103 kJ.
Puissance ( kW) = énergie ( kJ) / durée ( s).
Durée = 2,00 103 / 120 ~ 16,7 s.
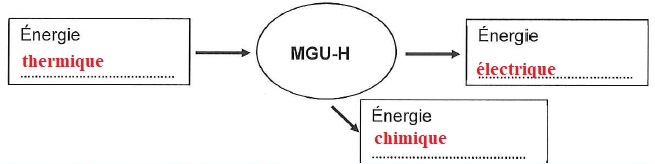
A.2.3 Compléter le document réponse DR1 de la page 18, en précisant les natures des énergies mises en jeu par le MGU-H.
|
|
|
|
|
A.3. Performances mécaniques du véhicule
A.3.1 La longueur de ce circuit est de 4,655 km. En 2008, le
finlandais Kimi Räikkönen a réalisé un tour avec une vitesse moyenne
égale à 205,2 km.h–1. En 2014, le record du tour en course a
été réalisé, par l'allemand Sebastian Vettel, en 1 min 28,92 s. Qui a
été le plus rapide entre Räikkönen et Vettel ?
1 min 28,92 s = 88,92 s ; 4655 / 88,92 = 52,35 m / s soit 52,35 x3,6 = 188,5 km / h.
Le finlandais a été le plus rapide.
A.3.2
L’aérodynamique est la branche de la physique qui étudie l'influence de
l'air sur la vitesse des véhicules. En effet, bien qu'incolore, inodore
et d'une densité relativement faible, l'atmosphère terrestre se
comporte comme un milieu visqueux qui freine le mouvement des véhicules
en circulation. Plus précisément, l'atmosphère terrestre génère une
force physique qu'on appelle force de frottements de l'air ou traînée.
A.3.2.a À l'aide du document D5 de la page 14, calculer le coefficient de traînée, CX, d'une Formule 1 sachant que la traînée valait T = 430 daN à la vitesse v = 313 km.h–1 à Barcelone en 2014.
T = 0,5 rair S Cx v2.
v = 313 / 3,6 = 86,94 m /s ; rair =1,18 kg m-3. S = 1,60 m2.
Cx = 4300 x 2 / (1,18 x1,6 x86,942) =0,603.
A.3.2.b
Le coefficient de traînée d'une Renault Clio Il vaut 0,32. À l'aide de
la question A.3.2.a et du document D5 de la page 14, dire quel véhicule
possède le meilleur aérodynamisme.
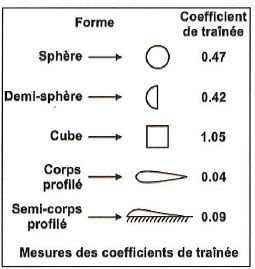
Plus le coefficient de traînée est faible, plus la traînée est faible et meilleur est l'aérodynamisme.
La clio possède le meilleur aérodynamisme.
A.3.3 La Formule 1 est à vitesse constante, v = 313 km.h–1, à la fin de la longue ligne droite.
Le poids de la Formule 1 vaut P = 690 daN.
Tracer, à l'échelle indiquée, sur le document DR2 de la page 18, les
vecteurs qui représentent respectivement le poids du véhicule, la
réaction normale du sol, la force motrice et la traînée. On les
appliquera conventionnellement au centre de gravité, G.
La vitesse étant constante et le mouvement rectiligne, ces 4 forces se compensent.
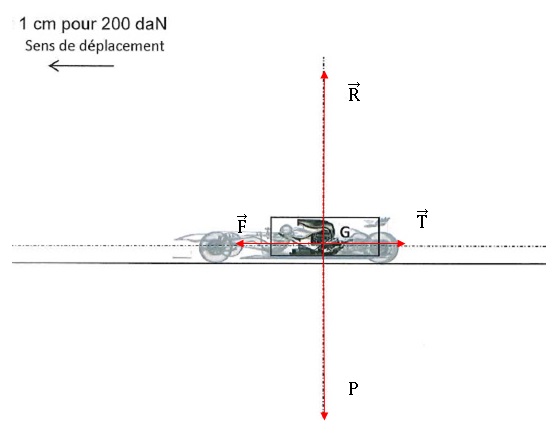
Poids : 690 daN soit 690 / 200 = 3,45 cm ; traînée : 430 / 200 = 2,15 cm.
A.3.4 Le constructeur annonce une puissance motrice maximale de 560 kW. Calculer la puissance mécanique, pméca, de la force motrice, F = 4,30 kN, en fin de la ligne droite du circuit de Barcelone sachant que pméca = F × v. Donner le résultat en kilowatts (kW). Le moteur était-il en régime maximal ?
pméca = F v = 430 x 86,94 = 3,74 105 W = 374 kW, valeur inférieure à 560 kW.
Le moteur n'est pas en régime maximal.
A.3.5 Les drapeaux
sont utilisés en Formule 1 pour transmettre des informations aux
pilotes. Ce sont les commissaires de course qui agitent ces
drapeaux sur le bord des pistes. Le drapeau rouge signifie
l'interruption de la course. Le pilote aperçoit un commissaire de
course agiter un drapeau rouge
sur le bord de la piste à la fin de la ligne droite. Le travail mécanique des forces de freinage, Wfrein, sera-t-il un travail moteur ou résistant ? Quelle est
l'unité d'un travail mécanique ?
La force de freinage est de sens contraire au déplacement. Le
travail de la force de freinage est résistant. Le travail s'exprime en
joule.
A.3.6 En appliquant
le théorème de l'énergie cinétique,calculer le travail mécanique, W,
des forces mises en jeu pour un arrêt complet du véhicule ayant une
masse m = 702 kg. Donner le résultat en mégajoule (MJ).
Le poids et l'action normale du plan étant perpendiculaires au
déplacement, elles ne travaillent pas. Seule la force de freinage
travaille. Son travail est égal à la variation de l'énergie cinétique.
W =0-½mv2= -0,5 x702 x86,942 = -2,65 106 J = -2,65 MJ.
Si le système de récupération MGU-K absorbe 2,00 MJ, calculer l'énergie
qu'il faut encore dissiper par frottement dans les freins.
2,65 -2,00 = 0,65 MJ..
|
|
PARTIE B – LA FORMULE E, DE LA F1 MAIS 100 % ÉLECTRIQUE !
B.1. Performances électriques de la batterie
B.1.1 Calculer la capacité (appelée aussi charge électrique), C1, de la batterie principale en ampère-heure (A.h).
La batterie est chargée en 90 minutes ( 1 ,5 heures) et l'intensité est égale à 128 A.
C1 = 128 x1,5 = 192 Ah.
B.1.2 La batterie
ne peut alimenter directement le moteur à courant alternatif de la
Formule 1. L'emploi d'un onduleur est donc nécessaire.
B.1.2.a Quelle est
la fonction de l'onduleur dans la chaîne énergétique allant de la
batterie au moteur ? Choisir parmi les propositions ci-dessous et
écrire la bonne réponse sur votre copie :
• il convertit un courant alternatif en courant alternatif ;
• il convertit un courant continu en courant alternatif ;
• il convertit un courant alternatif en courant continu.
B.1.2.b Après un réglage technique à l'atelier, l'allure du courant, i, débité par l'onduleur a été représentée ci-dessous.
Calculer la fréquence, f, de ce courant.
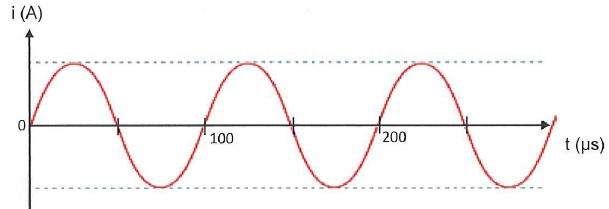
La période T est égale à 100 µs = 1,00 10-4 s.
La fréquence f vaut : f = 1 /T = 1,00 104 Hz.
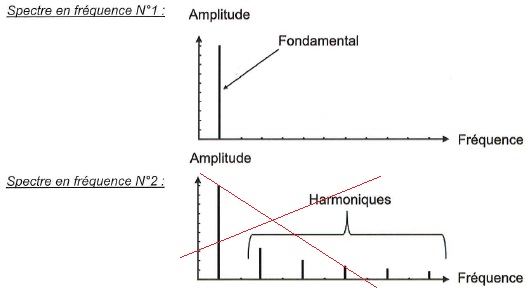
B.1.2.c Quel spectre en fréquence du document suivant correspond au courant, i, débité par l'onduleur ? Justifier la réponse.
Un courant sinusoïdal n'a pas d'harmoniques.
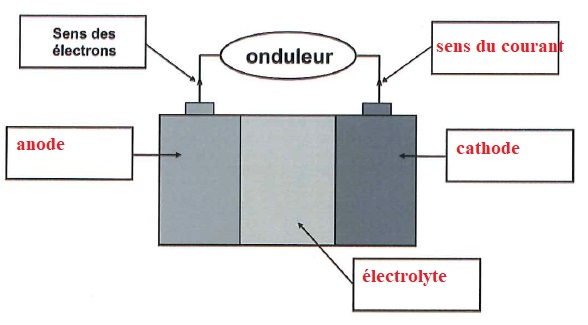
B.1.3
Quelles que soient les technologies utilisées, toutes les batteries ont
des parties communes appelées cathode, anode et électrolyte. Pour une
cellule lithium-ion, l'atome de lithium, Li, initialement à l'électrode
négative migre sous forme ionique, Li+, vers l'électrode positive à travers l'électrolyte lors d'une décharge. Compléter le schéma avec les quatre termes ci-dessous :
Cathode Anode Électrolyte Sens du courant.
B.1.4 Une nouvelle
génération de batteries rechargeables, jouissant d'une autonomie
largement supérieure à celles en vigueur actuellement, devrait
apparaître dans les prochaines années.
B.1.4.a Écrire la demi-équation d'oxydation du lithium, Li, qui a lieu à l'anode.
À l’anode, on observe une oxydation : Li = Li+ + e–.
B.1.4.b Recopier et compléter sur votre copie la demi-équation de réduction ci-dessous qui a lieu à la cathode :
O2 + 2 Li+ + 2 e– = Li2O2.
B.1.4.c Écrire l'équation globale équilibrée d'oxydoréduction.
2Li =2 Li+ + 2e–.
O2 + 2 Li+ + 2 e– = Li2O2.
Ajouter et simplifier. O2 + 2 Li = Li2O2.
B.1.5 Le métal commun aux batteries actuelles et futures est le lithium. Expliquer pourquoi le lithium est un produit dangereux.
Le liyhium est corrosif et inflammable.
B.2. Performances mécaniques du moteur.
B.2.1 Préciser sur votre copie quelle unité, parmi les propositions ci-dessous, caractérise l'intensité d'un champ magnétique B.
Tesla (T) ; Électronvolt (eV) ; Sievert (Sv) ; Gray (Gy).
B.2.2 Sachant qu'un tour du rotor correspond à une rotation d'un angle de 2p rad,
B.2.2.a Calculer tout d'abord la vitesse angulaire, W (en rad.s–1), du rotor. Le rotor peut tourner à n= 4000 tr / min et fournir un couple T = 140 N m.
N = 4000 tr.min–1 = 4000 / 60 = 66,67 tr / s.
W = 2 x 3,14 x 66,67 = 419 rad / s.
B.2.2.b Calculer ensuite la puissance mécanique, Pmoteur = T × W, fournie par le moteur en kilowatts (kW).
Pmoteur = 140 × 419 = 5,86.104 W = 58,6 kW.
B.2.3 Les
rendements des moteurs électriques sont des facteurs très importants.
Un très bon rendement permet une meilleure gestion de l'énergie lors
d'une course. Calculer les puissances électriques absorbées, Pa1 et Pa2, pour différents moteurs ayant respectivement des rendements h1 = 90,0 % et h2 = 95,0 % si la puissance mécanique fournie par chaque moteur électrique vaut Pmoteur = 60,0 kW.
Pa1 = Pmoteur / rendement = 60,0 / 0,900 = 66,7 kW.
Pa2 = Pmoteur / rendement = 60,0 / 0,950 = 63,2 kW.
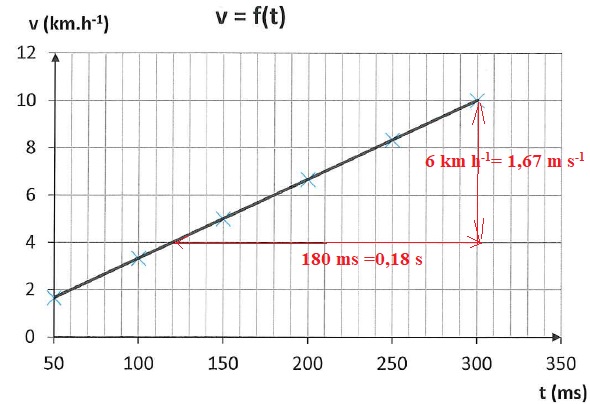
B.2.4 Les vitesses au cours du temps, mesurées après le départ d'une Formule E, sont reportées sur le graphique suivant.
B.2.4.a Démontrer que l'accélération, aFE, de la Formule E, est constante et vaut aFE = 9,1 m.s–2.
La
vitesse est une fonction affine du temps. L'accélération est la dérivée
de la vitesse par rapport au temps. L'accélération est donc constante
et vaut :
1,67 / 0,18 = 9,26 m s-2.
 . .
B.2.4.b Dans les mêmes conditions, une Formule 1 aurait eu une accélération aF1 = 13,9 m.s–2. Calculer et comparer les durées nécessaires pour passer de 0 à 100 km.h–1 pour une Formule 1 et une Formule E en admettant que les accélérations restent constantes.
100 km / h = 100 / 3,6 =27,78 m /s.
27,78 / 13,9 =2,00 s ; 27,78 / 9,26 =3,00 s.
B.3. Performances acoustiques
B.3.1 Quel est le nom de l'unité qui a pour symbole « dB » ?
Décibel.
Préciser sur la copie quel appareil, parmi les propositions ci-dessous, mesure un niveau sonore :
dynamomètre ; sonomètre ; microphone ; anémomètre.
B.3.2 Le seuil de douleur est atteint lorsque l'intensité sonore dépasse Iseuil = 10 W.m–2
à nos oreilles. Montrer qu'une personne présente au bord de la piste,
lors du départ d'une course de Formule 1, doit s'équiper de protections
auditives. Le niveu sonore LF1 est égal à 140 dB.
I = I0 1014 = 10-12 x 10140 / 10 = 100 W m-2, valeur supérieure 10 W.m–2
Il faut donc s’équiper de protections auditives.
B.3.3 Dans les mêmes conditions, l'intensité sonore reçue lors des qualifications d'une Formule E vaut IFE = 1,0 × 10–4 W.m–2.
B.3.3.a Donner la
durée d'exposition maximale, Δt., conseillée pour quelqu'un travaillant
sur le bord d'une piste lors d'une course de Formule E.

L = 10 log (1,0 10-4 / (1,0 10-12) = 10 log( 108) = 80 dB.
D’après le tableau, la durée maximale d’exposition est de 8h.
B.3.3.b Quelle est la différence de niveau sonore, ΔL, entre une Formule 1 et une Formule E ?
140-80 = 60 dB.
PARTIE C – UN SPORT SOUS HAUTE SURVEILLANCE
C.1. Les radiocommunications
C.1.1 Supposons que l'onde radiophonique ait une fréquence de 1,00 × 1010 Hz. Préciser à quel domaine, allant des BF aux EHF, elle appartient.

f = 1,00.1010 Hz = 10,0.109 Hz = 10,0 GHz.
Cette fréquence est située dans le domaine SHF.
C.1.2 Les
radioamateurs fans de Formule 1 peuvent utiliser comme récepteur une
antenne « quart d'onde » pour intercepter les communications entre les
coureurs et les stands. Montrer que la dimension de l'antenne, ℓ, est alors de 7,5 mm.
Longueur d’onde : c / f = 3,0 108 / 1010 = 3,0 10-2 m = 30 mm..
La longueur de l’antenne doit être égale au quart de la longueur d’onde : ℓ =30 / 4 = 7,5 mm.
C.2. Avant la course.
C.2.1 En 2016, à
Barcelone, la masse du monocoque de Renault Sport F1 était égale à m =
702 kg (avec pilote). Sachant que l'intensité de la pesanteur terrestre
est g = 9,81 N.kg–1, calculer l'intensité de la force, F, exercée par chacun des quatre pneus sur le sol. Exprimer le résultat en kilonewtons (kN).
Le poids du monocoque et P = m × g = 702 × 9,81 = 6 886,62 N ≈ 6,89.103 N.
Cette force est répartie sur les quatre pneus, donc F = P /4 = 1,72 kN.
C.2.2 La mesure
d'un manomètre numérique, effectuée par un juge pour vérifier la
pression des pneus d'une Formule 1 avant les qualifications, indique Pmesure = 1,348 bar. Indiquer au juge de piste si la voiture peut démarrer. Justifier votre réponse.
L’incertitude vaut (0,25 % x1600 ± 1 digit : 1,348 x 0,25 / 100 ~0,004 bar.
0,004 bar avec le digit, on arrive à 0,005 bar.
Donc Pmesure = 1,348 ± 0,005 bar soit [1,343 : 1,353 bar ].
La pression minimale des pneus arrière autorisée est de 1,35 bar.
La valeur 1,350 bar étant incluse dans la zone d’incertitude, la voiture peut être autorisée à démarrer.
C.2.3 La pression atmosphérique vaut Patm
= 1,00 bar. Or, il peut arriver qu'un pneu crève en course. Quelle est
alors la pression absolue du pneu une fois la voiture revenue aux
stands.
Si le pneu est crevé, la pression est égale à la pression atmosphérique.
C.3. En course
C.3.1 Compléter les phrases suivantes par une des trois propositions : augmente, reste la même, diminue.
• Lors de la course, la température des pneus augmente.
• Lors de la course, l'énergie interne du gaz de gonflage augmente.
• Lors de la course, la pression des pneus augmente.
• En supposant que la masse du véhicule reste identique lors de la course, la surface de contact du pneu avec la route diminue.
• Lors de la course, l'adhérence du pneu diminue.
C.3.2 À l'aide des relevés télémétriques du débitmètre ,expliquer si l'écurie sous surveillance doit être sanctionnée ou pas.
Le débit ne doit pas dépasser 100 kg.h-1, soit 100 x1000 / 3600 = 100 / 3,6 = 27,8 g / s.
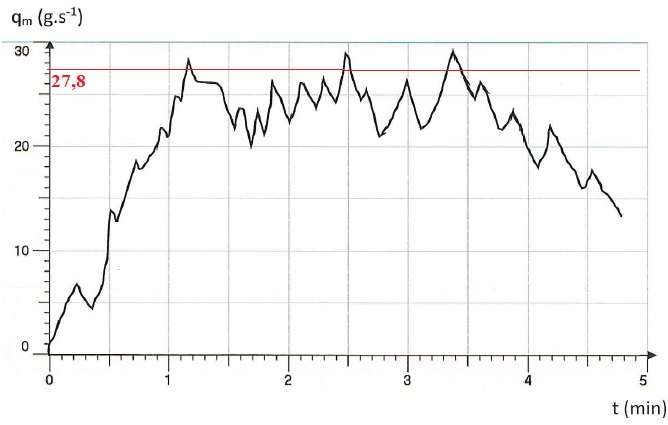
L'écurie doit être sanctionnée, le débit à dépassé plusieurs fois 27,8 g / s..
|
|