Physique chimie, radiographie, cure thermale Bac STI2D biotechnologie Métropole 09 / 2018

Physique chimie, radiographie, cure thermale, Bac STI2D STL biotechnologie Métropole 09 / 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Partie A - La radiographie.
A.1. Ondes électromagnétiques et radiographie.
A.1.1. Rappeler la structure d’une onde électromagnétique.
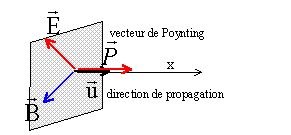
Une onde électromagnétique comporte un champ électrique et un champ magnétique oscillant à la même fréquence. Ces champs, perpendiculaires l'un par rapport à l'autre, se propage selon une direction orthogonale. Cette onde se propage avec une vitesse qui dépend du milieu.

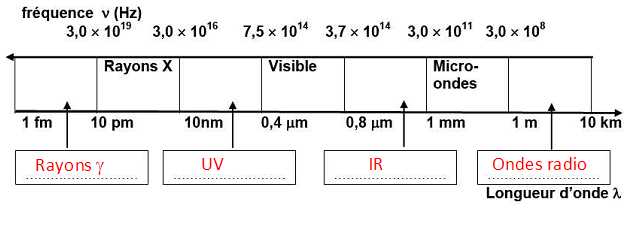
A.1.2. Compléter le spectre des ondes électromagnétiques en associant à chaque numéro le domaine des ondes électromagnétiques correspondant et choisi parmi les suivants : micro-ondes, lumière visible, ondes hertziennes, ultraviolets, rayons gamma, infrarouges.

A.1.4. Expliquer les variations de contraste observées sur l’image obtenue.
La radiographie enregistre l'image d'un corps traversé par un faisceau de rayons X. Suivant la constitution du corps, les rayons X sont plus ou moins absorbés et le film photographique, placé derrière le corps radiographié, est ainsi plus ou moins impressionné.
Les os absorbent fortemment les rayons X et apparaissent en blanc.
Les tissus absorbent peu les rayons X et apparaissent en gris.
A.1.5. L’appareil radiographique produit des rayons X d’énergie E = 120 keV.
A.1.5.1. Calculer la fréquence n des photons émis lors de l’examen radiographique.
E = 1,2 10⁵ x1,6 10^-19 =1,92 10^-14 J.
Fréquence n = E / h = 1,92 10^-14 / (6,62 10^-34) = 2,90 10¹⁹ Hz.
A.1.5.2. Déterminer la longueur d’onde dans le vide l des photons émis et vérifier qu’ils appartiennent au domaine des rayons X.
l = c / n = 3,00 10⁸ / (2,90 10¹⁹) =1,03 10^-11 m.
Cette valeur est comprise entre 10^-8 m et 10^-12 m ; ces photons appartiennent au domaine des rayons X.
A.2. Dose de rayonnement X reçue par madame K
L’appareil radiographique émet par seconde 8,0 × 10⁹ photons d’énergie E = 120 keV chacun.
A.2.1. Montrer que la patiente reçoit une dose D d’environ 90 μGy lors de cette radiographie qui dure Δt = 10 s sachant que la masse m de la partie du corps
irradiée est d’environ 17 kg.
Energie totale reçue : E = 1,20 10⁵ x1,6 10^-19 x8,0 10⁹ x10 = 1,536 10^-3 J.
Dose reçue = E / m = 1,536 10^-3 / 17 = 9,04 10^-5 Gy ~90 µGy..
A.2.2. Vérifier par le calcul que la dose équivalente reçue ED respecte la limite autorisée.
ED = 9,04 10^-5 x0,12 = 1,08 10^-5 Sv.
Cette valeur est très inférieure à 1 mSv, dose anuelle maximale.
A.3. Radioprotection du personnel médical
Pour se protéger, la manipulatrice radio porte un tablier contenant du plomb. L’absorption d’un rayonnement électromagnétique par un écran dépend de l’énergie des photons émis, du matériau utilisé et de l’épaisseur de l’écran.
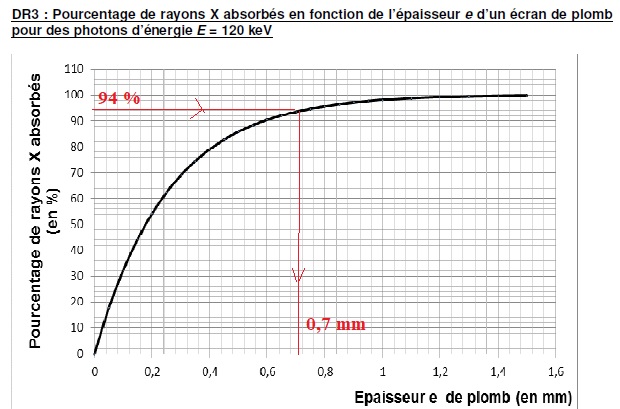
Le document suivant donne le pourcentage de rayonnement X absorbé en fonction de l’épaisseur e d’un écran de plomb pour des photons d’énergie E = 120 keV. Déterminer l’épaisseur e de plomb du tablier utilisé pour obtenir un pourcentage d’absorption de 94 %.

PARTIE B : Le trajet jusqu’au centre thermal.
Madame K vient d’acheter récemment une voiture diesel. Elle a remarqué que sa consommation moyenne est de 3,30 L de gazole pour 100 kilomètres parcourus et souhaite vérifier si cette dernière satisfait à l’objectif fixé par l’Union européenne pour 2020 concernant la pollution au CO₂, à savoir une émission de 95 g de CO₂ produit par kilomètre parcouru.
Le gazole est un carburant fossile constitué d’un mélange de différents composés miscibles. Pour simplifier, on l’assimilera à un alcane de formule brute C₂₁H₄₄.
Donnée : masse volumique du gazole : r = 845 g · L^-1 ;
B.1.1. Déterminer le volume V_g de gazole consommé par kilomètre parcouru.
3,3 / 100 = 0,033 L.
B.1.2. En déduire que la quantité de matière n de gazole consommé par kilomètre parcouru est de 9,42 × 10^-2 mol.
masse de 0,033 L de gazole : m = 0,033 x 845 = 27,885 g.
Masse molaire de C₂₁H₄₄. M = 21 x12 +44 = 296g / mol.
Quantité de matière de gazol n = m / M = 27,885 / 296 ~9,42 × 10^-2 mol.
B.1.3. Recopier sur la copie l’équation de combustion du gazole dans le dioxygène de l’air et l’équilibrer.
C₂₁H₄₄ + 32. O₂ ---> 21 CO₂ + 22. H₂O
B.1.4. Déterminer la quantité de matière n(CO₂) de dioxyde de carbone rejeté pour un parcours d’un kilomètre.
n(CO₂)= 21 x 4,92 10^-2 =1,98 mol.
B.1.5. La voiture de madame K satisfait-elle l’objectif fixé
n(CO₂) x M(CO₂)=1,98 x 44 ~87 g, valeur inférieure à 95. l'objectif est respecté.

PARTIE C : Siège élévateur pour personne à mobilité réduite
L’accès à la piscine du centre thermal a été aménagé pour permettre aux personnes à mobilité réduite d’accéder au bassin. Un moteur alimenté par une
batterie permet de déplacer verticalement une plateforme élévatrice.
Données constructeur :
- La plateforme de masse à vide m = 53,0 kg peut supporter une charge de masse maximale de 150 kg et permet de descendre d’une hauteur h = 1,44 m.
- La durée totale de montée ou de descente est de Δt = 18 s.
- La batterie délivre une puissance moyenne P = 80 W pour un fonctionnement à vide (sans charge).
Un watt·heure vaut 3 600 joules : 1 W h = 3 600 J
On donne l’intensité de pesanteur terrestre : g = 9,81 N · kg^-1.
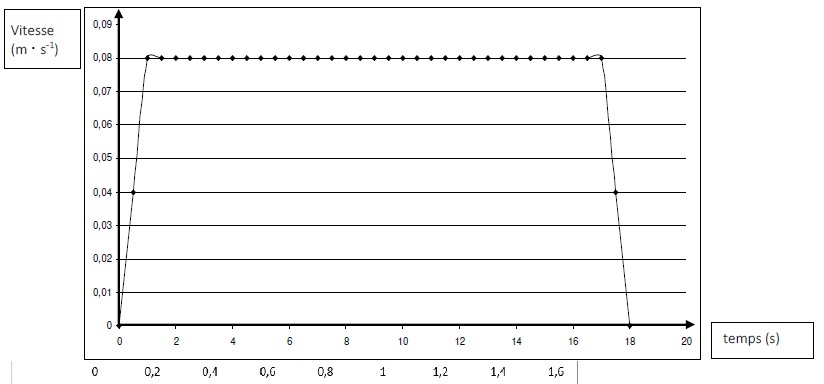
Le document ci-dessous décrit l’évolution de la vitesse de la plateforme en fonction du temps :

Dans toute cette partie, on étudie le mouvement de la plateforme à vide.
C.1.1. Vérifier que la vitesse maximale v_max du siège, lue sur le graphe, est compatible avec les données du constructeur sur la durée de montée.
h / Dt = 1,44 / 18 =0,08 m /s =v_max.
C.1.2. Sur le graphe, identifier les phases de démarrage et d’arrêt. Comment peut-on qualifier le mouvement entre ces deux phases ?
Phase de démarrage : entre 0 et 1 s ; phase d'arrêt : entre 17 et 18 s.
Entre ces deux phases le mouvement est uniforme ( la valeur de la vitesse est constante).
C.1.3. Citer les forces appliquées sur la plateforme pendant une montée.
Poids, poussée d'Archimède due à l'eau et force motrice exercée par le moteur.
C.1.4. Que peut-on dire de la résultante de ces forces entre t₁ = 1,0 s et t₂ = 17 s ?
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces appliquées sur la plate-forme est nulle.
C.1.5. Déterminer la variation de l’énergie mécanique ΔE_m de la plateforme lors d’une seule montée du siège.
L'énergie cinétique est nulle ( vitesse nulle au départ et à la fin).
L'origine de l'énergie potentielle étant prise au point le plus bas, la variation d'énergie potentielle vaut :
ΔE_m = 0-mgh = -53x9,81 x1,44 ~749 ~-7,5 10² J.
C.1.6. En raisonnant sur les unités, indiquer parmi les 3 expressions proposées ci-dessous la relation correcte entre l’énergie et la puissance :
E = P · Δt ; E = P / Dt ; E = P² · Δt
C.1.7. Déterminer l’énergie E fournie par la batterie lors d’une seule montée du siège.
P Dt = 80 x 18 =1,44 10³ J.
C.1.8. Expliquer pourquoi l’énergie E fournie par la batterie est supérieure à l’énergie mécanique reçue par la plateforme.
Une partie de l'énergie est dissipée sous forme thermique ( frottement ).

PARTIE D : Eau thermale et soins
D.1. À propos de l’eau thermale
L’eau thermale est une eau de type sulfurée sodique. Elle se caractérise principalement par :
- une faible minéralisation (0,18 g · L^-1),
- la présence de sulfures sous les formes de sulfure d’hydrogène H₂S, d’ions hydrogénosulfure HS^- ou d’ions sulfure S^2-,
- la dominance de la teneur en sodium (ions Na⁺).
Données :
masse volumique de l’eau : r_eau
liquide = 1,0 × 10³ g · L^-1 ;
pH de l’eau thermale : pH = 9,3 ;
température de l’eau thermale : environ 25°C.
- Le sulfure d'hydrogène est un composé chimique de formule H₂S. C'est un gaz acide, incolore, à l'odeur nauséabonde d'oeuf pourri et très toxique par inhalation à partir d’un seuil de 14 mg · m⁻³.
Il réagit avec les solutions aqueuses basiques et les métaux tels que l'argent.
- Couples acide / base : H₂S / HS^- ; HS^- / S^2-.
D.1.1. Citer deux méthodes permettant de mesurer le pH d’une solution.
L'Indicateur de papier pH donne un valeur approximative.
Le pHmètre donne une valeur précise.
D.1.2. L’eau thermale est-elle acide, basique ou neutre ? Justifier la réponse.
A 25°C, l'eau est basique, son pH ( 9,3) est supérieur à 7.
D.1.3. Déterminer la concentration en ions oxonium H₃O⁺ dans cette eau thermale et en déduire la concentration en ions hydroxyde HO^-.
[ H₃O⁺] = 10^-pH = 10^-9,3 = 5,0 10^-10 mol/ L.
[HO] = 10^-14 / [ H₃O⁺] =10^-14 / ( 5,0 10^-10)=2,0 10^-5 mol /L.
D.1.4. Les produits ménagers anticalcaires contiennent des espèces chimiques acides.
D.1.4.1 Donner la définition d’un acide selon la théorie de Brönsted.
Un acide est une espèce, ion ou molécule, susceptible de céder un proton H⁺.
D.1.4.2. Écrire l’équation chimique de la réaction entre l’ion hydrogénosulfure HS^- et l’ion oxonium H₃O⁺, espèce acide du couple H₃O⁺/H₂O.
HS^- + H₃O⁺ =H₂O + H₂S..
D.1.4.3. À quel désagrément s’expose-t-on en ajoutant un produit ménager anticalcaire avec de l’eau thermale ? Justifier.
Dégagement de H₂S, gaz acide, incolore, à l'odeur nauséabonde d'oeuf pourri et très toxique par inhalation.

D.2. Un exemple de soin ORL : douche nasale

- Le dispositif est composé :
- d’une cuve en verre de volume V = 3,0 L, munie à sa base d’un tuyau souple dont l’autre extrémité est raccordée à
un tube en inox permettant de brancher le tube nasal du patient.
- d’un robinet R en inox qui permet de régler le débit de l’eau thermale isotonique*.
*Eau thermale isotonique : eau thermale dans laquelle on a ajouté m = 10,0 g de sel par litre d’eau thermale.
- La prescription du médecin : Douche nasale d’eau thermale isotonique de deux litres :
- un litre par narine pendant quatre minutes.
Éviter tout mouchage violent pendant la douche nasale et ainsi que dans la demi-heure qui suit.
- Données : masse volumique eau thermale isotonique : r = 1,01 × 10³ kg · m^-3 ;
pression atmosphérique : P_A = P_atm = 1,02 × 10⁵ Pa ;

D.2.1. En appliquant le principe fondamental de l’hydrostatique entre les points A et B, déterminer la pression P_B au point B lorsque le robinet du dispositif est fermé.
P_B -P_A = r g AB =1,01 10³ x9,81 x0,25 = 2477 Pa ;
P_B = 1,02 10⁵ + 2477 = 1,045 10⁵ ~1,04 10⁵ Pa.
D.2.2. Madame K ouvre le robinet R pour effectuer son soin ORL.
D.2.2.1 D’après la prescription, montrer que le débit volumique de l’eau thermale isotonique pour ce soin est D_v = 4,2 × 10^-6 m³ · s^-1.
1 L = 10^-3 m³ ; 4 min = 4 x60 = 240 s.
10^-3 / 240 = 4,2 × 10^-6 m³ · s^-1.
D.2.2.2. Sachant que la vitesse d’écoulement v_A au point A est de 5,3 × 10^-4 m · s^-1, déterminer le diamètre de la cuve d_A au point A.
Section du tube ; S = D_v / v_A = 4,2 × 10^-6 / (5,3 × 10^-4 ) =7,924 10^-3 m² ;
d_A = (4 x7,924 10^-3 / 3,14)^½ ~0,10 m.

D.3. Un autre soin thermal : l’aérobain
Ce soin consiste à immerger le corps de la patiente dans une baignoire à bulles remplie d’eau thermale à une température q₁ = 36°C durant Δt = 10 min. Le volume d’eau thermale dans la baignoire est V_b = 240 L.
Avant que madame K s’immerge, on vérifie la température du bain : le thermomètre affiche q₂ = 38°C, il est donc nécessaire d’ajouter une masse m_f d’eau froide que l’on se propose de déterminer.
Données : capacité thermique massique de l’eau c_eau = 4,2 × 10³ J · kg⁻¹ · °C⁻¹ ;
masse volumique de l’eau : r = 1 000 kg · m^-3.
On rappelle que l’énergie échangée sous forme de chaleur Q lors d’une variation de température Dq pour un corps de masse m et de capacité thermique massique c s’écrit : Q = m · c · Dq.
D.3.1. Calculer l’énergie Q_P perdue par l’eau présente au départ dans le bain pour passer de la température 38°C à la température 36°C.
Q_P = 240 x4,2 10³ x(-2) = -2,016 10⁶ ~ -2,0 10⁶ J.
D.3.2. En négligeant les pertes thermiques, montrer que la masse m_f d’eau froide à rajouter au bain de madame K pour le refroidir est de 25 kg.
Energie gagnée par l'eau froide à 17°C : m_f x4,2 10³ (36-17) = 7,98 10⁴ m_f J.
m_f = 2,016 10⁶ / (7,98 10⁴) ~25 kg.
D.3.3. Le débit du robinet d’eau de la baignoire étant D_vrob= 20 L · min^-1, pendant quelle durée Δt le robinet d’eau froide doit-il rester ouvert pour refroidir à 36°C l’eau du bain de madame K ?
25 / 20 = 1,25 min = 1 min 15 s.