Le kiiking,
sport extrème, Bac S Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Il
s'agit pour le sportif de faire un tour complet sur des structures
métalliques. Debout, ses pieds sont attachés à une planche reliée à des
cables en acier, le tout formant un ensemble rigide. Le reccord
correspond à une longueur de tige de 7,15 m.
L'étude est faite dans le référentiel terrestre considéré comme galiléen. Les forces de frottement sont négligeables.
1. Modélisation du mouvement de la structure.
Le sportif est assimilé à un point matériel de masse m = 80 kg relié à
une tige de longueur L = 7,15 m. Le système, modélisé comme un pendule
simple est écarté de sa position d'équilibre d'un angle qi et abandonné sans vitesse initiale.
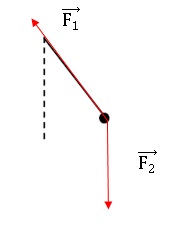
1.1.
Le schéma ci-dessous représente le système à deux instants distincts :
position au repos et passage par sa position d'équilibre. Nommer les
forces qui s'exercent sur le système. Attribuer une légende aux cas 1
et 2. Justifier à l'aide d'une loi de Newton que l'on énoncera.

Cas n° 2 :Première loi de Newton.
Dans
un référentiel galiléen, si la somme vectorielle des forces extérieures
appliquées à un solide est nulle ( solide pseudo-isolé ) alors le
centre d’inertie G de ce solide est soit au repos, soit animé d'un
mouvement rectiligne uniforme et réciproquement.
Cas n°1 : deuxième loi de Newton.
Dans
un référentiel galiléen, la somme vectorielle des forces extérieures
appliquées à un solide est égale au produit de la masse M du solide par
l'accélération de son centre d'inertie.
1.2
Représenter les forces qui s'exercent sur le système dans une position
quelconque. Que peut-on dire du vecteur vitesse de celui-ci ?
Le vecteur vitesse est tangent à la trajectoire circulaire et a le sens du mouvement.
On définit un repère (O, x, y ) où O est la position d'équilibre du système.
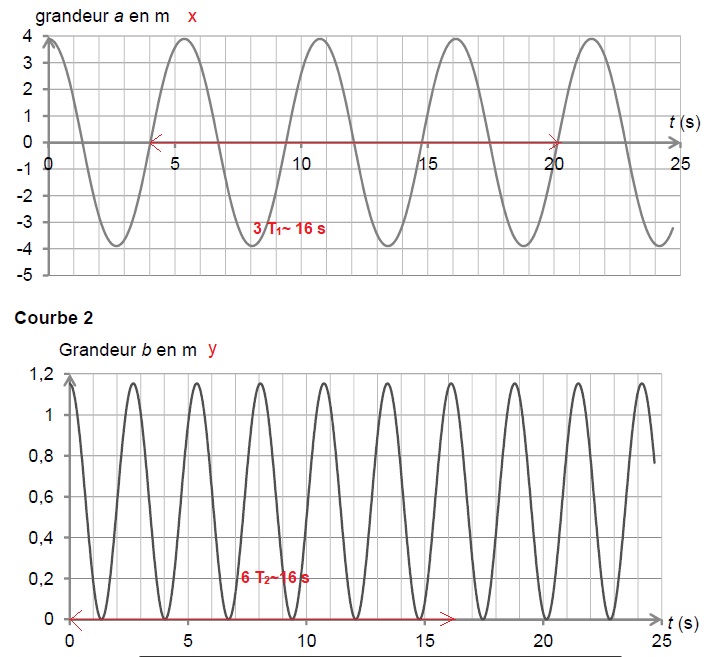
1.3. Les
enregistrements indiquant les variations des coordonnées x et y
en fonction du temps t sont donnés. Identifier, en justifiant la
coordonnées x ou y correspondant à la grandeur a, puis déterminer la
période T1 de ses variations. Déterminer la période T2 des variations de l'autre coordonnée.
Calculer la période propre T du pendule simple.
Justifier qualitativement la relation simple liant T1 et T2.
La grandeur y est toujours positive ; la grandeur x est positive ou négative.
T1 ~16 / 3 ~5,3 s ; T2 ~ 16 / 6 ~2,7 s ; T1 = 2 T2.
T = 2 p (L /g)½ = 2 x3,14 (7,15 / 9,81)½ =5,36 s.
|
|
2. Etude énergétiique du mouvement.
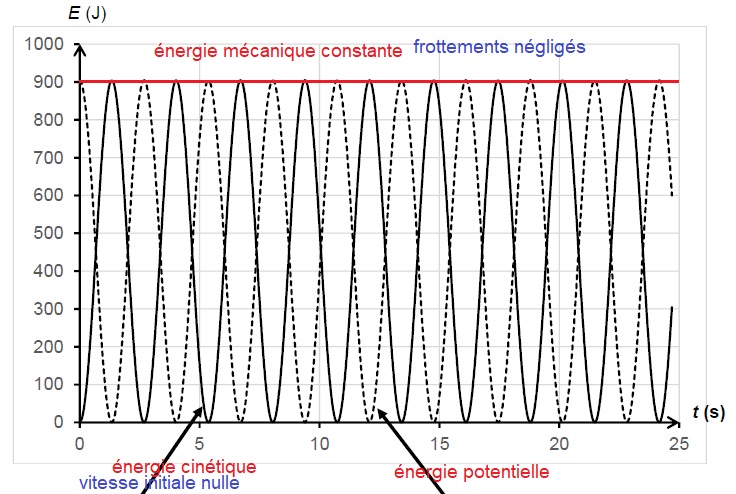
Variations des énergies en fonction du temps.
2.1. Les enregistrements débutent au moment du lâcher du système. Identifier les courbes en justifiant.
Rappeler l'expression de l'énergie mécanique du système et tracer la courbe Em = f(t). Justifier son allure.
L'énergie mécanique est la somme des énergie cinétique et potentielle.
Em = ½mv2 + mg y.
|
|
2. 3. Montrer que l'expression de l'énergie potentielle de pesanteur du système est Epp = mgL ( 1 - cos a).
L'origine de l'énergie potentielle est nulle à la position d'équilibre stable.
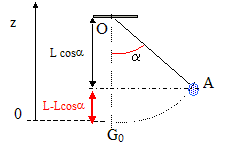
Epp = mgz = m g
L(1-cos a)
avec L =OA en mètre
2.4. Déterminer l'angle a au moment du lâcher.
L'énergie potentielle initiale vaut 900 J.
900 = mgL ( 1 - cos a) ; cos a = 1-900 / (mgL).
cos a = 1-900 /(80 x9,81 x7,15) = 0,84 ; a ~33°.
3. Vitesse nécessaire pour effectuer un tour complet.
3.1. Quelle vitesse minimale ( en km / h) au point O est-il nécessaire pour effectuer un tour complet ?
Au point le plus haut a = p.
Epp = mgL ( 1 - cos 180) = 2 mgL
Energie mécanique en O : ½mv2.
Conservation de l'énergie mécanique.
½mv2 = 2mgL ; v = (4gL)½ =2 (9,81 x7,15)½ = 16,75 m /s.
Soit 16,75 x3,6 ~60,3 km /h.
3.2 . Lors d'une chute libre de hauteur h, la vitesse atteinte au sol est v = (2gh)½.
Vérifier
que la vitesse précédente correspond à celle atteinte lors d'une chute
libre de hauteur maximale atteinte par le sportif.
Hauteur maximale atteinte : h = 2 L = 14,3 m.
(2gh)½ = (2 x9,81 x14,3)½ =16,75 m /s.
|
|