Nuisances
sonores sous-marines, Bac S Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
1. Paramètres influençant la vitesse du son dans l'eau de mer.
1.1. Etude de la salinité.
La salinité S d'une eau de mer est proportionnelle à la chlorinité notée Cl.
S = 1,80655 Cl.
La chlorinité est la masse de chlore ( exprimée en g ) présente dans 1 kg d'eau de mer.
On prépare 50,0 mL d'eau de mer diluée au dixième. On appelle Smer
cette solution. On réalise un titrage conductimétrique de 10,0 mL de
cette solution par une solution titrante de nitrate d'argent de
concentration c1 = 5,0 10-2 mol/L.
Equation de la réaction modélisant la précipitation des ions chlorure :
Ag+aq + Cl-aq --> AgCl(s).
1.1.1 Proposer un protocole de préparation de 50 mL de solution Smer.
Prélever 5,0 mL d'eau de mer à l'aide d'une pipette jaugée.
Verser dans une fiole jaugée de 50,0 mL.
Compléter avec de l'eau distillée jusqu'au trait de jauge.
Boucher et agiter pour rendre homogène.
1.1.2. Interpréter le changement de pente observé sur le graphe suivant.
1.1.3. Vérifier que la salinité de l'échantillon est voisine de 35 g / kg.
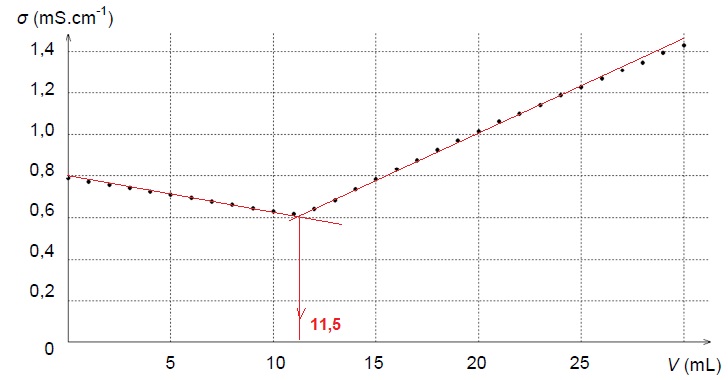
Avant l'équivalence, l'ion argent est en défaut : du point de vue
de la conductivité, tout se passe comme si on remplaçait l'ion chlorure
par l'ion nitrate de conductivité moindre. La conductivité de la
solution décroît.
Après l'équivalence, l'ion argent est en excès. On ajoute des
ions argent et des ions nitrate, la conductivité de la solution croît
rapidement.
A
l'équivalence : quantité de matière d'ion chlorure = quantité de
matière d'ion argent = 11,5 x 0,050 = 0,575 mmol dans 10 mL de Smer.
Soit 0,575 / 10 = 0,0575 mol /L.
Tenir compte de la dilution : 10 x0,0575 = 0,575 mol d'ion chlorure par litre d'eau de mer.
ou 0,575 x35,5 = 20,4 g d'ion chlorure par litre d'eau de mer.
Densité de l'eau de mer d = 1,023.
20,4 / 1,023 = 19,95 g d'ion chlorure par kg d'eau de mer.
S = 19,95 x1,80655 ~36 g / kg.
|
|
.
.
|
|
|
|
|
1.2. Mesure de la vitesse du son à une profondeur donnée.
v ~ 1410 +4,21 q-0,037q2 +1,10 S +0,018 P.
q : température en degré Celsius ; P profondeur en mètre ; Salinité g / kg.
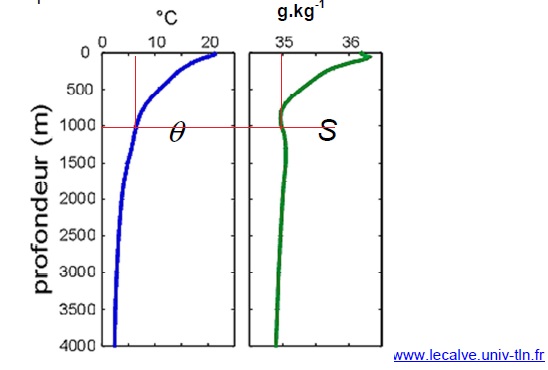
Montrer que l'approximation " les sons se propagent environ 5 fois plus
vite dans l'eau que dans l'air " est justifiée lorsqu'on se trouve dans
l'eau à une profondeur de 1000 m.
v ~ 1410 +4,21 x 7-0,037 x 72 +1,10 x35 +0,018 x1000 ~1,49 103 m/s soit environ 5 x3 102, vitesse du son dans l"air
|
|
2. Risques auditifs pour les dauphins.
Pour communiquer les dauphins produisent des sifflements dont la
fréquence peut varier entre 1,1 kHz et 24 kHz et qui peuvent posséder
jusqu'à 11 harmoniques. Le seuil de risque auditif pour les cétacés est
de 220 dB à 3 kHz.
2.1.1. Les ondes émises par les dauphins sont des ondes progressives mécaniques. Que signifie ces deux derniers termes ?
Propagation d'une perturbation dans un milieu matériel sans transport de matière, avec transport d'énergie.
2.1.2. Les sifflements des dauphins sont-ils audibles par l'homme ? Justifier.
L'oreille humaine perçoit les sons de fréquences comprises enntre 20 Hz
et 20 kHz. Seuls les sifflements des dauphins dont les fréquences sont
comprises entre 1,1 kHz et 20 kHz sont audibles pour l'oreille humaine.
2.1.3. Déterminer la longueur d'onde de l'onde ultrasonore correspondant à un sifflement de fréquence 24,9 kHz émis par un dauphin.
l = v / f = 1500 / (24,9 103) ~6,0 10-2 m.
2.1.4. Calculer la valeur de la fréquence des trois premières harmoniques de ce sifflement.
f2 = 24,9 x2 = 49,8 kHz ; f2 = 24,9 x3 = 74,7 kHz ; f2 = 24,9 x4 = 99,6 kHz.
2.2. Impact du son émis par un sonar.
Certains sonars émettent des sons d'intensité sonore 3,2 1011 W m-2 pour une fréquence de 3 kHz.
2.2.1. Montrer que le signal du sonar correspond à un niveau d'intensité sonore de 235 dB.
L = 10 log ( I / I0) = 10 log( 3,2 1011 / (1,0 10-12)) = 235 dB.
2.2.2. Le son est atténué de 0,16 dB km-1
dans l'eau de mer. Estimer la distance minimale à laquelle un dauphin
peut se trouver sans subir de risque auditifs. Que penser de ce
résultat ?
(235-220) / 0,16 ~94 km.
Il est probable que des dauphons se trouvent à une distance inférieure
à 94 km du sonar et subissent des risques auditifs.
2.2.3. Le sous- marin se rapproche du dauphin à une vitesse de 22,0 km /h et envoie une onde acoustique de 3 kHz.
Le son perçu par le dauphin est-il plus grave ou plus aigu ? Justifier.
Le sous marin et le dauphin se trouvent à la même profondeur. Calculer la valeur du décalage Doppler et commenter.
fR -fE = vE / v fE est positif.
fR > fE , le son reçu est plus aigu lors de l'approche.
22,0 / 3,6 = 6,1 m /s.
fR -fE = vE / v fE = 6,1 / 1500 x 3 103 =12,2 Hz.
|
|