La caféine
dans le thé, Bac S métropole 09/2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Dans cet exercice, on s’intéressera
à la caféine présente dans le thé et au nombre de tasses de thé qu’un
adulte peut boire par jour sans risque pour la santé.
Données : masse molaire moléculaire de la caféine : MCAF
= 194 g.mol-1 ;
pour une personne en bonne santé, le risque d’intoxication à la
caféine existe pour une consommation de plus de 400 mg de caféine par
jour pendant une durée prolongée.
1. Caractéristiques
de la caféine
La formule topologique de la molécule de caféine est donnée ci-contre :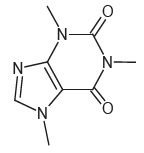
1.1. Représenter la
formule semi-développée de la caféine.
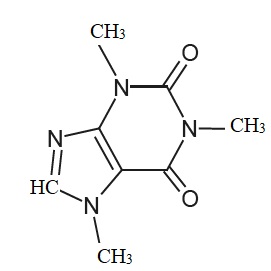
1.2. Justifier que
le spectre RMN de la caféine présente quatre singulets.
La molécule possède quatre groupes de protons, donc 4 signaux. Les
carbones voisins des atomes de carbones porteurs de ces protons ne
portent aucun proton, donc 4 singulets..
2.
Nombre de tasses de thé qu’un adulte peut boire par jour
L’objectif de cette partie est d’évaluer le nombre de tasses de thé du
commerce qu’un adulte peut boire par jour sans risque pour la santé.
Pour cela, on souhaite réaliser un dosage spectrophotométrique de la
caféine présente dans une infusion de thé. Le spectre UV de la caféine
obtenu
après son extraction d’une infusion de thé par du dichlorométhane est
donné.
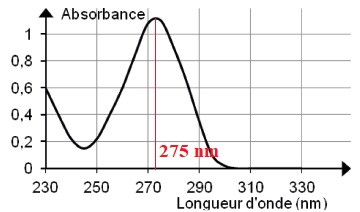
2.1. Estimer la
valeur de la longueur d’onde optimale à laquelle le spectrophotomètre
pourrait être réglé pour réaliser les mesures d’absorbance lors du
dosage. Justifier.
Pour un maximum de précision, on travaille à la longueur d'onde
correspondant au maximum d'absorption.
2.2. Sachant que le
dichlorométhane est incolore et que l’absorbance de la caféine est
quasiment nulle pour des longueurs d’onde supérieures à 330 nm,
indiquer si la caféine est une espèce colorée dans le dichlorométhane.
L'absorbance de la caféine étant nulle dans le domaine visible ( 400 ;
800 nm), le solvant étant incolore, la solution est incolore.
|
|
On dissout de la caféine en poudre dans du
dichlorométhane afin de préparer 100 mL d’une solution S0 de
caféine de concentration molaire C0 = 5,7 × 10-4
mol.L-1.
2.3. Déterminer la
valeur de la masse de caféine qui a été dissoute dans le
dichlorométhane afin d’obtenir 100 mL de solution S0.
Quantité de matière de caféine : n = 5,7 10-4 x 0,100 = 5,7
10-5 mol.
Masse de caféine m = MCAF n = 5,7 10-5 x 194 =
0,011 g = 11 mg.
On prépare par dilution de la solution S0 quatre autres
solutions S1, S2, S3, S4
dont on mesure l’absorbance à la longueur d’onde retenue. Les mesures
sont reportées sur le graphe ci-dessous.
2.4. Choisir, en
justifiant la réponse, parmi les 4 lots de verrerie suivants, celui qui
permet de préparer avec précision la solution S3 de
concentration molaire en caféine égale à C3 = 5,7×10-5
mol.L-1.
Facteur de dilution F = C0 / C3 = 10.
Le volume de la fiole jaugée doit être 10 fois plus grand que celui de
la pipette jaugée. Donc lot n° 1.
Lot
|
1
|
2
|
3
|
4
|
Verrerie
|
Pipette
jaugée de 2,0 mL
Fiole jaugée de 20,0 mL.
|
Pipette
jaugée de 5,0 mL
Fiole jaugée de 20,0 mL. |
Pipette
graduée de 10 mL
Fiole jaugée de 20,0 mL. |
Eprouvette
graduée de 5 mL
Fiole jaugée de 50,0 mL. |
.
|
|
2.5. Une infusion de thé est
préparée en introduisant un sachet de thé du commerce dans une tasse
contenant de l’eau chaude. L’emballage conseille une durée d’infusion
de deux minutes. Au bout de ces deux minutes, on retire le sachet et on
laisse l’infusion de thé refroidir. La caféine de l’infusion est
extraite à
l’aide de 100 mL de dichlorométhane. On considère que la totalité de la
caféine a été extraite par le dichlorométhane et qu’elle est contenue
dans
ce volume V = 100 mL.
Trop concentrée pour une mesure d’absorbance, la solution de caféine
dans le dichlorométhane obtenue est tout d’abord diluée 10 fois.
L’absorbance de cette solution diluée est mesurée à la longueur d’onde
retenue et on obtient A = 0,43.
En se limitant au critère lié à la quantité de caféine, évaluer le
nombre maximal de tasses de ce thé qu’un adulte pourrait boire par
jour. Commenter.
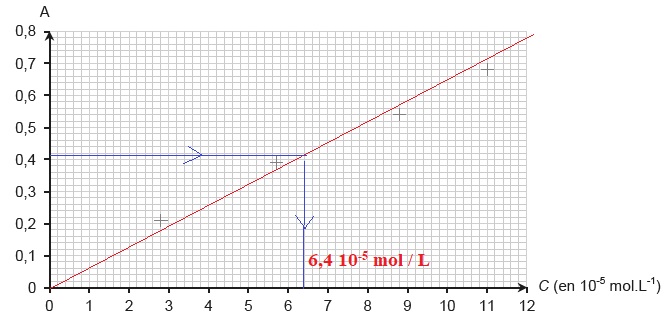
Compte tenu de la dilution, la concentration de caféine dans la tasse
est 6,4 10-4 mol/L.
Quantité de matière correspondante n = 6,4 10-4 x0,100 = 6,4
10-5 mol.
Masse de caféine dans une tasse : n MCAF = 6,4 10-5
x194 = 0,012 g ou 12 mg.
Nombre de tasses de thé : 400 / 12 ~33 soit un volume de 3,3 L.
Il est improbable qu'une personne boive 3,3 L de thé chaque jour.
|
|