Détecteurs
de fumée, bac S Nlle Calédonie 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
......
.....
|
Afin de
prévenir des risques d’incendies, l'installation de détecteurs de
fumées est obligatoire dans tous les logements depuis janvier 2016. Il
existe différents types de détecteurs comme les détecteurs optiques ou
les détecteurs ioniques.
Dans cet exercice, on étudiera ces deux types de détecteurs de fumées,
puis on s’intéressera au choix de l’emplacement du détecteur dans le
cadre de la protection des personnes.
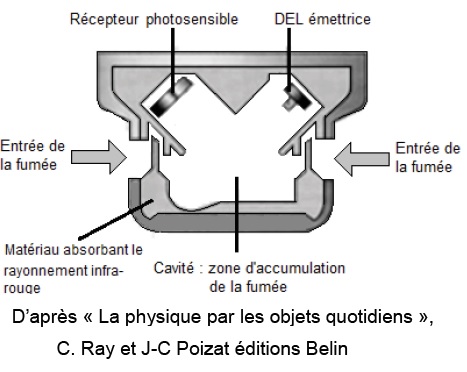
1. Détecteur optique de fumées
Le principe de fonctionnement de ce détecteur de fumées repose sur le
fait qu’une diode électroluminescente (ou DEL) produit en continu un
rayonnement. Lorsqu’il rencontre des particules de fumées, le
rayonnement est dévié dans toutes les directions. Un récepteur
photosensible détecte alors le rayonnement et génère un courant
électrique qui déclenche une alarme sonore avertissant les usagers de
la présence de fumées.
La longueur d’onde du rayonnement émis par la DEL dépend du matériau utilisé pour sa fabrication. Pour produire un rayonnement
infrarouge, on peut utiliser de l'arséniure de gallium (GaAs). Dans ce cas, l’énergie des photons émis est de l’ordre de 1,4 eV.
1.1. Le récepteur photosensible ne détecte que les rayonnements appartenant au domaine de l’infrarouge.
Vérifier que le rayonnement lumineux émis par la DEL utilisée dans le détecteur optique de fumées appartient bien à ce domaine.
E =1,4 eV = 1,4 x1,6 10-19 =2,24 10-19 J.
Longueur d'onde l = h c / E =6,63 10-34 x3,0 108 /(2,24 10-19) ~8,9 10-7 m ~0,89 µm.
Cette valeur est supérieure à 0,80 µm, elle appartient au proche infrarouge.
1.2. On admet que les particules solides présentes dans la fumée ont une taille comprise 0,1 μm et 100 μm.
Quel phénomène physique peut contribuer à la déviation du faisceau lumineux si des fumées sont présentes ? Justifier.
Certaines particules
contenues dans les fumées ont des dimensions du même ordre de grandeur
que la longueur d'onde du rayonnement de la diode. Ces particules
peuvent diffracter le rayonnement de la diode.
1.3.
En présence de fumées, le rayonnement émis par la DEL est dévié dans
toutes les directions. Expliquer brièvement pourquoi l’alarme ne se
déclenche qu’en présence de fumées.
Le détecteur
photosensible ne détecte pas le rayonnement de la diode en absence de
fumées. Par contre il détecte une partie du rayonnement de la diode en
présence de fumées ; il convertit ce rayonnement en courant électrique.
|
...
|
|
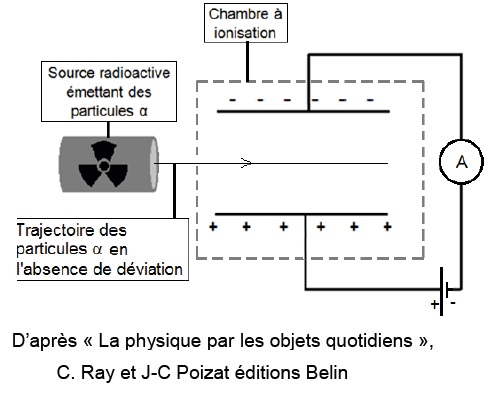
2. Détecteur ionique de fumées
Le principe de ce détecteur de fumées repose sur l’ionisation de l’air par des particules α. En l’absence de fumées, ces particules arrachent des électrons
aux molécules de dioxygène et de diazote présentes dans la chambre à ionisation. Pour le dioxygène, l’ionisation nécessite un apport d’énergie de 12 eV
par molécule. Les ions et les électrons formés par l’ionisation de l’air sont soumis à un champ électrique uniforme entre deux plaques. Un courant électrique de faible
intensité apparaît alors dans le circuit électrique
Lorsque la fumée pénètre dans la chambre à ionisation, une partie des électrons et des ions issus de l’ionisation se fixe aux poussières de fumées. La baisse de l’intensité du courant électrique qui en résulte déclenche un avertisseur sonore.
Données :
1 électronvolt (eV) = 1,6 x 10-19 J ;
charge élémentaire : e = 1,6 x 10-19 C ;
pour un condensateur plan, le champ électrostatique E est reliée à la tension U et à la distance d quisépare les plaques par la relation : E = U /d ;
charge de la particule α : qα = + 2 e ;
masse d’une particule α : mα = 6,64 x 10-27 kg ;
intensité du champ de pesanteur terrestre : g = 9,81 m.s-2.
On s’intéresse au mouvement d’une particule α arrivant dans la chambre à ionisation en l’absence de fumée. Cette particule arrive en un point O avec un
vecteur vitesse initiale v0 parallèle aux plaques C et D du condensateur plan.
Une tension constante U = 9,0 V est appliquée entre les deux plaques C et D ( d = 3,0 cm). La valeur de la vitesse initiale v0 est égale à 1,6 × 107 m.s-1.
On étudie le mouvement de la particule α dans le référentiel terrestre supposé galiléen. À l’instant t = 0, la particule α est au point O.
Lors de cette étude, on négligera les éventuelles collisions avec les molécules de l’air ainsi que la valeur du poids de la particule α devant la valeur de la force électrostatique Fe F subie par cette particule.
2.1. Vérifier quantitativement que l’hypothèse concernant le poids de la particule α est justifiée.
Poids : P = ma g = 6,64 10-27 x9,81 ~6,51 10-26 N.
Force électrique : F = 2e E = 2e U / d = 2 x1,6 10-19 x9 / 0,03 =9,6 10-17 N, valeur très supérieure au poids.
2.2. Reproduire sur la copie le schéma de la figure puis y représenter le champ électrostatique E et la force électrostatique F que subit la particule α au point O. Justifier.
Le champ électrique pointe vers le plus petit potentiel, celui de la plaque C chargée négativement.
Les vecteurs force électrique et champ sont colinéaires et de même sens, la charge étant positive.
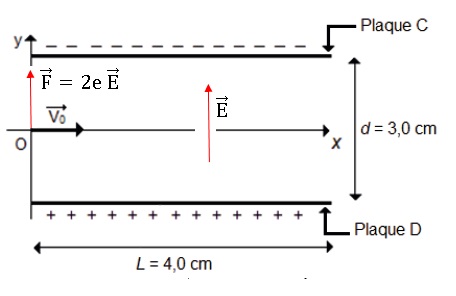
2.3. Établir les équations horaires du mouvement de la particule α .
Vecteur accélération : ( 0 ; 2eE / ma )
Vecteur vitesse, primitive du vecteur accélération : ( v0 ; 2eE / ma t )
Vecteur position, primitive du vecteur vitesse : x = v0 t ; y = eE / ma t2 = eU / (ma d) t2 .
2.4. Déterminer la valeur de la coordonnée yL de la particule lorsqu’elle a parcouru une distance suivant l’axe Ox égale à L = 4,0 cm. Expliquer pourquoi le mouvement de cette particule peut être considéré comme rectiligne dans la chambre d’ionisation.
t = L / v0 = 0,040 / (1,6 107) ~2,5 10-9 s.
yL = 1,6 10-19 x9 /(6,64 10-27 x 0,03) x(2,5 10-9)2 ~2,8 10-8 m.
yL étant très inférieur à d, le mouvement de cette particule est quasiment rectiligne dans la chambre d'ionisation.
2.5. Montrer que l’énergie cinétique initiale des particules α est suffisante pour ioniser des molécules de dioxygène.
E = ½mav02 =0,5 x6,64 10-27 x(1,6 107)2 = 8,5 10-13 J soit 8,5 10-13 /(1,6 10-19) = 5,3 106 eV, valeur supérieure à 12 eV.
|
....
|
3. Niveau d’intensité sonore du détecteur de fumées
Une personne endormie est réveillée par un bruit dont le niveau d’intensité sonore est supérieur à 75 dB.
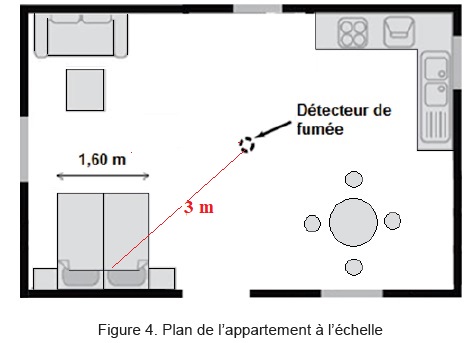
Un particulier souhaite installer un détecteur de fumées au plafond de
son appartement. Le niveau d’intensité sonore du détecteur de fumées
est de 85 dB à 3 m. Le particulier se demande si l’emplacement prévu
est judicieusement choisi.
Donnée :
Au cours de la propagation d’une onde sonore et en l’absence
d’atténuation, le niveau d’intensité sonore L diminue avec la distance
d à
la source S suivant la formule : L2 = L1 + 20 log (d1 / d2).
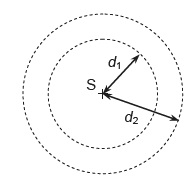
où L2 est le niveau d’intensité sonore mesuré à la distance d2 de la source et L1 le niveau d’intensité sonore
mesuré à la distance d1 de la source.
À l’aide du plan ci-dessus, schématisant la pièce, déterminer si
l’emplacement du détecteur est satisfaisant pour réveiller une personne.
On précise que la hauteur sous plafond est de 2,5 m dans l’appartement du particulier.
Remarque : pour cette étude, on négligera les phénomènes de réflexion du son sur les parois de la pièce.
d2 ~(32 +2,52)½~ 3,9 m.
L2 = L1 + 20 log (d1 / d2) = 85 +20 log(3 / 3,9) =82,7 dB, valeur supérieur à 75 dB.
L'emplacement du détecteur est satisfaisant.
|
|




