Tuyau d'orgue,
Bac S Antilles 09 / 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Les
orgues les plus imposantes peuvent comporter de 2000 à 4000 tuyaux
sonores. Certains tuyaux, comme ceux appartenant au jeu de « montre »,
sont ouverts à leurs deux extrémités. L’air est insufflé par une
soufflerie au niveau de leur base.
Un tuyau d’orgue de longueur L émet un son de hauteur déterminée qui dépend de la température ambiante.
Un musicien affirme que :
« Une augmentation de température de 10 °C modifie la hauteur de la note d’un quart de ton ! »
Dans ce problème, on souhaite valider cette affirmation. On étudie pour
cela la note jouée par un tuyau métallique à embouchure de flûte
appartenant à un jeu de « montre ».
Données :
Modèle théorique du tuyau ouvert/ouvert (ouvert aux deux extrémités)
lorsqu’une colonne d’air est excitée, un son est alors émis ;
la longueur d’onde du son émis est égale au double de la longueur du tuyau : l = 2.L
Relation entre célérité v du son et la température T de l’air : v = (11,64 T / M)½, T la température de l’air en Kelvin et M = 0,0289 kg.mol-1 la masse molaire de l’air.
Longueur du tuyau d’orgue étudié à 20 °C. L = 52,0 cm.
Questions préliminaires
1. Déterminer la
note jouée par le tuyau étudié. Le candidat cherchera à obtenir la
meilleure précision possible et s’assurera que les deux graphiques
(documents 1 et 2) sont cohérents.
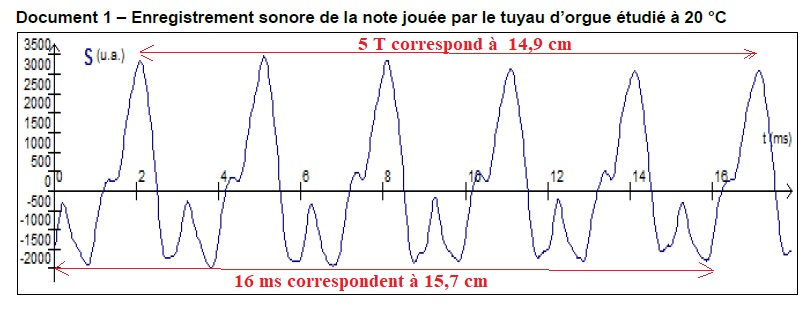
T = 14,9 x16 / (5 x15,7) = 3,04 ms ; fréquence 1 / t = 1000 / 3,04 = 329 Hz.

Fréquence du fondamental : f = 11,2 x1,4 / (3 x16) = 0,327 kHz = 327 Hz.
Les deux documents sont cohérents. La note jouée est le Mi3.
2. Discuter qualitativement l’influence d’une variation de température sur la hauteur du son produit.
La vitesse du son augmente si la température croït.
La longueur d'onde est constante égale à 2 L.
f = v / (2L) ; la fréquence va donc augmenter.
.
|
|
|
|
|
Problème.
3. Déterminer
quantitativement si l’affirmation du musicien sur l’évolution de la
hauteur du son est correcte. Un calcul numérique est attendu..
« Une augmentation de température de 10 °C modifie la hauteur de la note d’un quart de ton ! »
Variation correspondante de la vitese : v293= (11,64 T / M)½= (11,64 x293 / 0,0289)½ =343,53 m /s.
v303= (11,64 T / M)½= (11,64 x303 / 0,0289)½ =349,34 m /s.
349,34 -343,53 =5,8 m /s.
Variation correspondante de la fréquence : 5,8 / (2 x0,52) ~5,6 Hz.
Fréquence du Mi3 : 330 Hz ;
Fréquence du Fa : 349 Hz.
Un demi-ton sépare ces deux notes soit 19 Hz..
Un quart de ton au dessus du Mi3 correspond à la fréquence : 330 x 21/24~340 Hz
L'affirmation est fausse.
|
|
.
|
|