Autour du
papillon, Bac S Antilles 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
1. Etude du sonar de la chauve-souris.
La fréquence sonore émise par la chauve-souris est fe = 50 kHz.
1.1.1. A quel domaine de fréquence appartient l'onde émise par la chauve-souris ?
Domaine des ultra-sons.
1.1.2 Est-ce une onde mécanique ou électromagnétique ? Justifier.
La propagation des ultra-sons nécessite un milieu matériel. Les ultra-sons sont des ondes mécaniques.
1.2.1. Cette onde est-elle transversale ou longitudinale ? Justifier.
La direction de propagation de l'onde et la direction de déformation du milieu sont identiques. Il s'agit d'onde longitudinale.
1.2. En utilisant l'effet Doppler, il est possible d'évaluer la vitesse vCS de la chauve-souris. Pour une chauve-souris se rapprochant d'un récepteur d'ultra-sons, le dispositif mesure une fréquence fr =50,8 kHz, différente de la fréquence émise par la chauve-souris.
Montrer que la vitesse de la chauve-souris est proche de 19 km / h.
fr = fe Vonde / (Vonde-VCS) ; fr (Vonde-VCS) = fe Vonde ; VCS =(1- fe / fr )Vonde.
VCS = (1-50,0 / 50,8) x 340 = 5,35 m /s ou 5,35 x3,6 ~19 km / h.
1.2.2. Comparer Vonde à VCS. Expliquer en quoi ce résultat est important pour le déplacement ou la chasse de la chauve-souris.
Vonde est très supérieur à VCS.
La durée écoulée entre l'émission de l'onde et la perception de l'écho
reste donc très inférieure à la durée correspondante du déplacement de
la chauve-souris. La chauve-souris détecte ainsi l'obstacle et ne
risque pas de le heurter. La chauve-souris apprécie la distance la
séparant de la proie.
1.3. Le signal émis par la chauve-souris lui revient après une durée t = 16,7 ms. Estimer la distance qui sépare la chauve-souris du papillon.
2d = Vonde t = 340 x16,7 10-3 = 5,68 m ; d = 2,84 m.
2. La tactique défensive du papillon.
Le papillon se laisse tomber de la branche sur laquelle il se trouve
dès qu'il entend les émissions sonores des chauves-souris. Le papillon
peut-il se protéger par cette méthode d'une chauve-souris distante de d
= 2,8 m ?
On considère que le papillon est immobile au point C avant de se
laisser tomber de la feuille. On prend l'origine des temps, l'instant
ou le paipllon commence à se laisser tomber. Les frottements et la
poussée d'Archimède dans l'air sont négligés.
2.1.1. Etablir l'expression vectorielle du vecteur accélération du papillon.
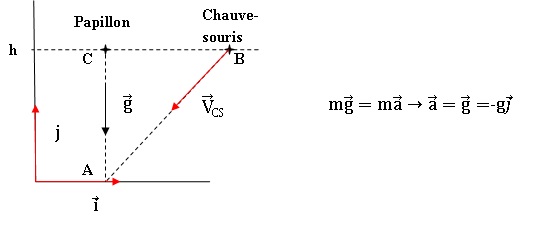
2.1.2. Etablir l'équation horaire z(t) du mouvement du centre d'inertie G du papillon.
La vitesse est une primitve de l'accélération et la vitesse initiale est nulle.
v = -g t.
La position est une primitive de la vitesse et l'altitude initiale est h.
z(t) = -½gt2 + h.
2.1.3. En déduire que l'expression de la durée de la chute est Dt = (2h/g)½.
Au sol z(t) = 0 ; .-½gDt2 + h = 0 ; Dt = (2h /g)½
2.1.4. Vérifier que cette expression est homogène à un temps.
h est un distance ( m) ; g une accélération ( m s-2) ; h / g s'exprime en s2 et (2h /g)½ s'exprime en seconde.
2.1.5. Calculer la durée nécessaire pour arriver au sol et être ainsi protégé. h = 1,2 m.
Dt = (2x1,2 / 9,8)½ = 0,4949 ~0,49 s.
2.2. On considère la vitesse de la chauve souris constante. Conclure quand à la tactique du papillon pour se protéger.
Distance parcourue par la chauve souris : (h2 + d2)½ =(1,22 +2,82)½ =3,046 m.
Durée de ce parcours : 3,046 / 5,35 ~ 0,57 s.
La chauve-souris arrive trop tard en A. Le papillon est protégé, sa tactique est efficace..
|
|
...
|
|
3. Le camouflage optique du papillon.
L'iridescence
est la propriété de certaines substances qui semblent changer de
couleur selon l'angle de vue ou d'éclairage. Elle est bien
visible sur les ailes de certains papillons. Dans le modèle élémentaire
suivant, on considère que :
- les écailles de l'aile du papillon sont assimilables à des couches minces à faces parallèles d'épaisseur constant e :
- les ondes issues des chemins 1 et 2 interfèrent au niveau de la rétine de l'observateur ;
- l'aile du papillon est éclairée par de la lumière.
e = 100 nm ; indice de la couche mince n = 1,5, indépendant de la longueur d'onde.
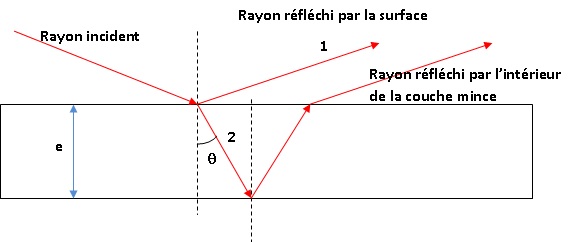
On note t le retard de l'onde qui a suivi le trajet 2 par rapport à celle qui a suivi le trajet 1.
|
|
3.1. Pour une onde lumineuse de période temporelle T, justifier qu'il y a interférences constructives pour t = k T et interférences destructives pour t = (k+0,5) T où k est un entier.
Les interférences sont constructives si la différence de marche entre les rayons 1 et 2 est égale à k' l = k' c T.
Les interférences sont destructives si la différence de marche entre les rayons 1 et 2 est égale à (k'+0,5) l = (k'+0,5) c T.
La différence de marche est proportionnelle à t.
3. Lorque la lumière blanche arrive perpendiculairement à la surface de l'aile, t peut s'écrire :
t = 2 n e / c +½T.
Quelles ondes
monochromatiques peuvent conduire à des interférences constructives ?
En déduire la couleur qui sera principalement perçue par l'observateur.
2 n e / c +½T = kT ; 2ne / c =( k-0,5)T ; 2ne = (k-0,5) cT = (k-0,5) l.
l =2ne /(k-0,5) =2 x1,5 x100 /(k-0,5) = 300 / (k-0,5) nm.
k = 1 ; l = 300 / 0,5 = 600 nm ( jaune orangé).
k = 2 ; l = 300 / 1,5 = 200 nm (domaine UV).
3.3. Lorsque la lumière blanche n'arrive pas perpendiculairement à la surface de l'aile, le retard a pour expression :
t = 2 n e cos q / c +½T.
Expliquer pourquoi la couleur de l'aile du papillon perçue par
l'observateur sera différente s'il le ragarde sous un autre angle.
2 n e cos q / c +½T = kT ; 2ne cos q / c =( k-0,5)T ; 2ne cos q = (k-0,5) cT = (k-0,5) l.
l =2ne cos q /(k-0,5) =2 x1,5 x100 cos q /(k-0,5) = 300cos q / (k-0,5) nm.
k = 1 ; q = 20° : l = 300 cos 20 / 0,5 = 563 nm ( vert jaune).
k = 1 ; q =45° : l = 300 cos 45 / 0,5 = 424 nm ( violet).
|
|