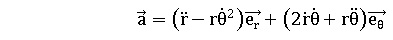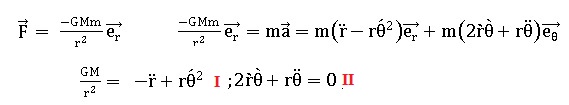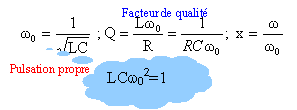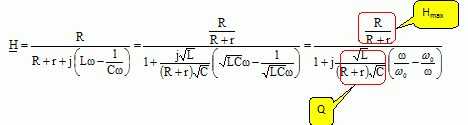Forces centrales, satellite, filtres, lunette de Galilée  Concours ITPE 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Orbites satellitaires. Le référentiel R (T, xyz) est supposé galiléen, son origine T coïncide avec le centre de masse de la terre. Tous les mouvements orbitaux de ce problème appartiennent au plan Txy. Dans ce plan les mobiles ponctuels considérés sont repérés par les coordonnées polaires r et q. 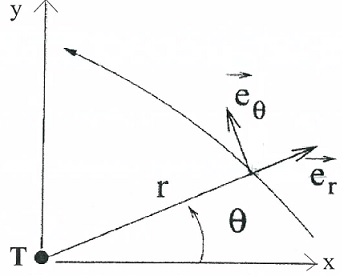1. Rappeler les expressions polaires de la vitesse et de l'accélération en fonction des coordonnées r et q, de leurs dérivées et des vecteurs unitaires. 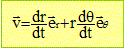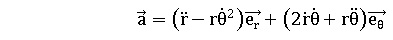2. Exprimer la force de gravitation exercée par la terre sur un corps ponctuel de masse m situé à la distance r du centre de l'astre. 3. Appliquer le principe fondamental de la dynamique à un corps ponctuel soumis à la seule force de gravitation. Montrer que l'on obtient les équations suivantes. 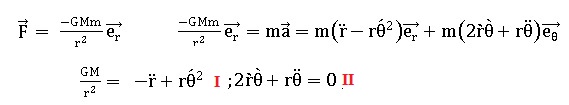4. En déduire de l'équation II que la quantité r2q' reste constante au cours du mouvement. Par la suite on posera C = r2q' . Multiplier par puis intégrer : 2r r' q' + r2q"=0 ; cette expression est la dérivée de  r2q' ; par suite, en intégrant r2q' = constante. 5. On considère tout d'abord un corps ponctuel dont le mouvement géocentrique est circulaire de rayon r1. 5.1. Justifier simplement que le mouvement est uniforme. Le corps n'est soumis qu'à la force de gravitation, orthogonale à chaque instant à la vitesse. Cette force ne travaille pas et l'énergie cinétique du corps reste constante. La valeur ( norme ) de la vitesse est donc constante et le mouvement est uniforme. 5.2. Etablir une expression entre la vitesse angulaire q', le rayon r1, G et la masse de la terre. I conduit à, r étant constant : GM / r12 = r1q'2 ; GM / r13 = q'2 . 5.3. Exprimer le rayon de l'orbite du corps autour de la terre en fonction de G, M et de la période T de révolution. Le corps décrit la circonférence 2pr1 en T seconde à la vitesse v = r1q' : 2pr1 = r1q' T = (GM /r1)½ T ; 4p2r12 = GM / r1 T2 ; r1 =[GM T2 / (4p2)]1/3. 5.4. On modèlise ainsi l'orbite d'un satellite géostationnaire. Donner la période de révolution d'un tel satellite. T = 24 h = 86400 s. 5.5. Calculer le rayon rG de l'orbite d'un satellite géostationnaire. rG  =[6,67 10-11 x6 1024 x864002  / (4x3,142)]1/3=4,2 107 m = 4,2 104 km. .... ..... 6. On revient au cas général. 6.1. Déduire des résultats établis aux questions 3 et 4 que le mouvement radial du corps, d'écrit par la distance r(t), est solution de l'équation différenteille  : m d2r /dt2 = m r" = F(r), ( 2) où F(r) est une force qui dérive de l'énergie potentielle "effective" Ep ef (r) = mC2 / (2r2) -GMm/r. I s'écrit : GM / r2= -r"+(r2q')2/ r3 ; r"= C2 / r3-GM / r2 ; mr"= mC2 / r3-GMm / r2 . F(r)= -Ep ef (r)  / dr soit F(r) = mC2 /r3 -GMm / r2. Par suite r" =F(r). 6.2. Montrer que l'équation (2) est associée à l'intégrale première : ½mr'2 +Ep ef (r) = Cste = Em. Par intégration de (2) il vient :  ½m r'2 = -Ep ef(r) + Cste. 7. 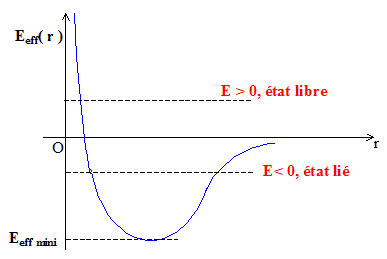L'allure de Ep ef(r) est représentée ci-dessous : 7.1. Déterminer les valeurs des distances r0 et r1 correspondants respectivement à l'annulation de Ep ef (r) et de d(Ep ef(r) / dr, les reporter sur la figure. Ep ef (r) = mC2 / (2r02) -GMm/r0 =0 ; C2 / (2r0) -GM =0 ; r0 =C2 / (2GM). d(Ep ef(r) / dr =0 ; F(r) = mC2 /r13 -GMm / r12=0 ; r1 = C2 / (GM). r1 corrpond au minimum de la courbe. 7.2. Décrire qualitativement le mouvement radial du corps dont l'énergie mécanique E serait égale à Eeff mini, E <0 et E >0. E>0 et e >1 : hyperbole ; E=0 et e=1 : parabole ; -Eeff mini < E <0 et 0<e<1 : ellipse ; E= -Eeff mini : cercle. 7.3. Retrouver le résultat établit en 5.2. r1 = C2 / (GM) et C = r12q'  ;  r1 = r14 q'2/ (GM) ; GM =  r13 q'2 . 8. La technique de lancement en orbite géostationnaire est la suivante : le satellite est placé en orbite circulaire basse puis le dernier étage est allumé pour placer le satellite sur une orbite elliptique (2) dont l'apogée se situe à environ 36 000 km appelée orbite de transfert géostationnaire. Enfin un moteur d'apogée à propergol solide solidaire du satellite circularise l'orbite (3). D'après Wikipédia. 8.1. Dans quel plan se trouve l'orbite géostationnaire ? Dans le plan équatorial. 8.2. Relier la valeur 36000 km à un résultat obtenu précédemment. 36 000 + Rterre = 4,2 104 km. 8.3. Représenter sur un schéma légendé les différentes orbites. 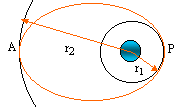géostationnaire : trajectoire circulaire dans le plan équatorial. en conséquence les deux autres orbites sont situées dans le plan équatorial. 8.3. A quels moments l'énergie mécanique varie ? Dans quel sens se fait cette variation ? l'énergie mécanique sur la trajectoire elliptique se conserve aux points A et P : E = - GMm / (r1 +r2). énergie mécanique sur l'orbite circulaire basse : au point P : E1 = -½ mGM / r1 variation d'énergie mécanique en P : DE = E -E1 = - GMm / (r1 +r2) + ½ mGM / r1 DE =GMm (r2 - r1) / [2(r1 +r2)r1]. DE est positive, la vitesse du satellite augmente. énergie mécanique sur l'orbite circulaire haute : au point A : E2 = -½ mGM / r2 variation d'énergie mécanique en A : DE = E2 -E = - ½ mGM / r2 +GMm / (r1 +r2) DE =GMm (r2 - r1) / [2(r1 +r2)r2]. 8.4 Aux différentes orbites, l'énergie mécanique est-elle du type -Eeff mini, E>0, E <0 ? Orbites circulaires : E = Eeff mini. Ellipse : -Eeff mini < E <0. Emissions satellitaires. Eutelsat2 West A est un satellite géostationnaire qui offre un service ITV et transmet une centaine de chaînes de télévision en clair dans plusieurs pays. Il émet à destination de petites antennes de réception situées chez les particuliers. les fréquences utilisées sont celles de la bande Ku (autour de 12 GHz). 1.  Quel est l'intérêt d'un satellite géostationnaire pour ce type de transmission ?. Ce satellite paraît fixe pour un observateur terrestre. 2. Calculer le temps de propagation de l'émetteur à un récepteur à la verticale du satellite. 36 000 / (3 105) = 0,12 s. 3. Dans quel domaine du spectre électromagnétique se trouve la bande Ku ? Ondes radioélectriques. 4. Donner les différents domaines du spectre électromagnétique. Indiquer pour chacun un ordre de grandeur de la fréquence et de la longueur d'onde. 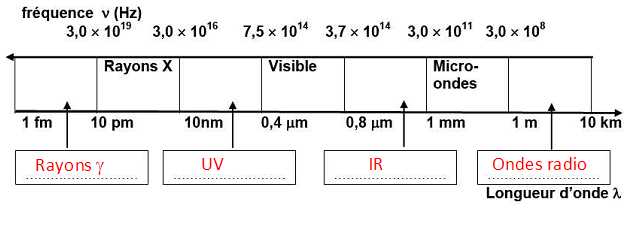5. Calculer la longueur d'onde d'une émission dans la bande Ku. l = c / f = 3 108 / (12 109)=.0,025 m.. 6. La taille minimale de l'antenne de réception est de l'ordre de grandeur de celle de la longueur d'onde du signal. Est-il possible d'utiliser une antenne plus petite ? La puissance reçue d'un satellite au niveau de la terre est très faible. Il faut concentrer cette énergie au moyen d'une antenne parabolique. En dessous de 60 cm de diamètre, de gros nuages qui passent  peuvent couper l'image et le son. 7. Approche quantique. 7.1. Calculer l'énergie E' d'un photon dans la bande Ku. E' = h n =6,63 10-34 x12 109 ~8 10-24 J ou 8 10-24 / (1,6 10-19) =5 10-5 eV. 7.2. Comparer cette énergie à celle d'un rayonnement ionisant ( 1 eV). E' est 20 000 fois plus faible que l'énergie d'un rayonnement ionisant. 7.3. Déterminer la quantité de mouvement p d'un photon de cette bande. p = E / c = 8 10-24 /(3 108) =2,7 10-32 kg m s-1. 7.4. Una antenne parabolique reçoit un signal de puissance P = 0,5 pW. Combien recoit-elle de photons par seconde ? Est-il possible de négliger l'aspect quantique pour se placer dans l'hypothèse d'un signal continu ? Energie reçue en une seconde : 5 10-13 J ; nombre de photons : 5 10-13 /(8 10-24) ~6 1010. Le signal peut être considéré comme continu. Traitement des signaux du satellite. 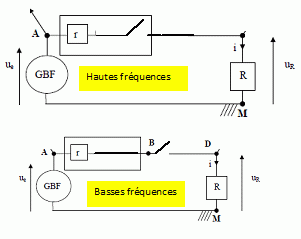Le signal reçu subit deux filtrages électroniques. 1. Le premier filtre peut être modélisé par une bobine d'inductance L, de résistance r, un condensateur de capacité C et une résistance R en série.La tension d'entrée ue est celle aux bornes du dipôle global RLC, la tension de sortie us est prise aux bornes de la résistance. 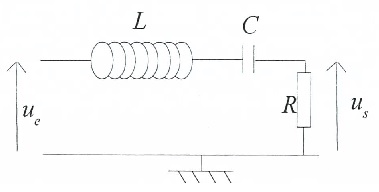1.1.1.Rappeler à quoi est équivalent un condensateur en basse fréquence, puis en haute fréquence. Même question pour la bobine. En basse fréquence un condensateur se comporte comme un interrupteur ouvert et en haute fréquence comme un interrupteur fermé. En basse fréquence une bobine se comporte comme un interrupteur fermé et en haute fréquence comme un interrupteur ouvert. 1.1.2. Déterminer la nature du filtre 1. Filtre passe bande. On notera w la pulsation de la tension sinusoïdale. 2.1. Quelle est la relation entre la fréquence et la pulsation d'une tension sinusoïdale ? w = 2pf. 2.2. Donner l'impédance complexe de chaque composant du filtre puis du dipôle équivalent au filtre. ZR = R  ; ZL = jLw ; ZC =1/ (jCw) ; Z = R + j(jLw -1/(Cw)). 2.3 Rappeler la définition de la fonction de transfert H du filtre. H = us / ue. 2.4 et 5 et 6 Exprimer H en fonction de L, C, R et w. 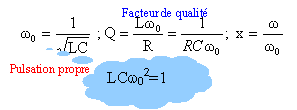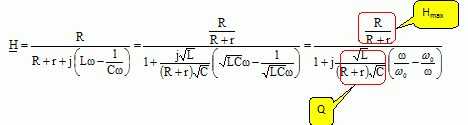2.7.1. On désire un filtre avec une fréquence propre f0 = 10 GHz. On dispose d'une capacité de 0,2 fF. Déterminer la valeur de l'inductance nécessaire. w0 = 2 x3,14 x1010 =6,28 1010 rad /s. LCw02 = 1 ; L = 1/(0,2 10-15 x(6,28 1010)2) =1,27 10-6 H= 1,27 µH. 2.7.2. On dispose de plusieurs inductances de 2 µH. Proposer un montage pour obtenir une inductance équivalente à 1 µH. Mettre deux inductances de 2 µH en dérivation. 2.7.3. On désire un facteur de qualité de 10000. déterminer la valeur de la résistance nécessaire. R = Lw0 / Q = 1,27 10-6 x6,28 1010 / 10000~8 ohms. 2.7.4. Quel pourrait être l'intérêt d'un haut facteur de qualité pour ce filtre ? Le filtre serait très sélectif. Le second filtre peut être modélisé par un condensateur de capacité C = 2,2 pF et une résistance R =470 ohms en série. 3.1. Proposer en justifiant par des arguments qualitatifs, un montage pour obtenir un filtre passe bas avec ces deux composants. 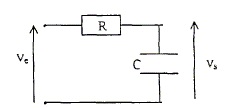A très basse fréquence le condensateur se comporte comme un interrupteur ouvert ( impédance infinie). Vs diffère de zéro. A haute fréquence, le condensateur se comporte comme un interrupteur fermé ( impédance nulle). Vs est nulle. Donc filtre passe bas. 3.2. Aux bornes de ce flitre, nous plaçons une source pure de tension E. Le condensateur est initialement déchargé. A t =0, E passe instantanément de la valeur 0 à la valeur 2 V. 3.2.1. Déterminer l'équation différentielle linéaire reliant ue, us à t >0. ue = Ri +us avec i =Cdus / dt. ue = RC dus / dt +us. 3.2.2. Montrer que l'on peut écrire cette équation sous la forme dus /dt +us / t = ue / t. ue /(RC)=  dus / dt +us/(RC). On pose t = RC. 3.2.3. Exprimer us en fonction de E. us= E(1-exp(-t / t)). 3.2.4. Exprimer en fonction de t le temps nécessaire t1 pour lequel us = 1,8 V. Calculer t1. 1,8 = 2(1-exp(t1 / t)) ; 0,9-1 = -exp(-t1 / t)) ; -ln 0,1 =t1 / t ; t1 = t ln 10. RC = 470 x 2,2 10-12 = 1,034 10-9 s ; t1 ~2,4 10-9 s. Observation des satellites. 4.1. Un oeil distingue deux points distants d'au moins 1 mm  à 3 m. Donner en degrés l'angle minimum de résolution de l'oeil. Est-il possible de distinguer deux satellites à 0,01 ° d'écart à l'oeil nu ? 1 10-3 / 3 = 3,33 10-4 rad ou 3,33 10-4 x180 / 3,14 =0, 2 °. On ne peut pas distinguer deux satellites à 0,01° d'écart. 4.2. Pour mieux les distinguer on utilise une lunette de Galilée  ( oculaire L1, f '1 = -4 cm ; objectif L2, f '2 = +10 cm).O1O2 = + 6 cm. 4.2.1. Donner le type et la vergence de chaque lentille. L1 divergente, 1 /(-0,04) = -25 dioptries ; L2 convergente, 1 / 0,10 = 10 dioptries. 4.2.2 et 3 et 4 et 5  Tracer le trajet optique de rayons lumineux provenant de l'infini parallèles à l'ace optique passant par L2. 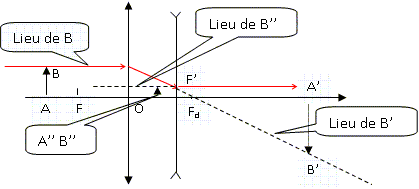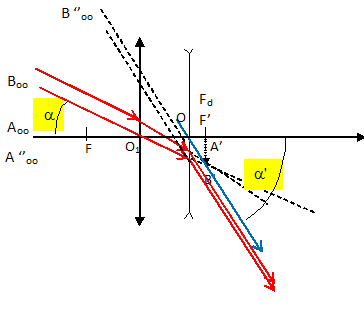2.6. Montrer que le grossissement G = a' / a = 2,5 si les rayons sont peu éloignés de l'axe optique. Les angles étant petits on assimile la tangente à l'angle exprimé en radian. G = a' / a avec a' = A'B' / OF' et a = A'B' / F'O1. G = F'O1 /OF' =10 / 4 = 2,5. 2.7. Sous quel angle a' pourra-t-on voir l'écart entre les satellites à 0,01 d'écart à travers la lunette ? 0,01 x2,5 = 0,025 °. L'oeil pourra les distinguer en regardant à travers la lunette.

menu