Physique,
Préparation au concours ingénieur territorial 2019.
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Calculs.
1. Conversions d'unités
Convertir dans l'unité demandée.
11,5 km = 11 500 m =11,5 103 m ; 120 g = 0,12 kg ; 1,67 10-6 cm = 1,67 10-5 mm ;
0,36 MW =3,6 105 W =3,6 1011 µW ; 1,35 m3 =1,35 103 dm3 =1,35 103 L ;
3,8 cm3 =3,8 10-3 L = 0,38 cL ; 4,7 mm2 = 4,7 10-6 m2 ;
7,2 km /h = 7,2 /3,6 m /s = 2 m /s ; 150 W m-2 =150 x1000 / 104 mW cm-2=15 mW cm-2.
2. La boite coule t-elle ?
Une boite tétraèdrique, vide à l'intérieur, est faite de 4 plaques
triangulaires identiques en cuivre d'épaisseur e ( négligeable devant
les dimensions de la boite ). Les triangles sont équilatéraux de côté a.
a. Exprimer la masse de la boite en fonction de a, e et rCu masse volumique du cuivre.
Hauteur d'un triangle : a x3½ / 2.
Surface d'un triangle : a2 x3½/ 4.
Volume d'un triangle : a2 x 3½ x e / 4
Masse d'un triangle : a2 x 3½ x e / 4x rCu.
Masse de la boite m= a2 x 3½ x e x rCu.
b. Exprimer la hauteur du tétraèdre en fonction de a.
h = a x 6½ / 3.
c. En déduire le volume de la boite.
V =1 /3 xbase x hauteur = 1 / 3 x a2 x3½ / 4 x a x 6½ / 3 =a3 x 2½ /12.
d. A partir de quelle épaisseur e la boite coule t-elle dans l'eau ? rCu = 8900 kg m-3.
Poids de la boite : P = 9,81 m.
Poussée d'Archimède due à l'eau à la limite de flotaison : V reau x9,81.
La boite coule si le poids devient supérieur à la poussée :
m > V reau ;
a2 x 3½ x e x rCu > a3 x 2½ /12 reau ;
e > a x 6½ / (36 x 8,9).
|
....
...
|
Mécanique.
1.
Le record du monde du marathon est de 2 h 2 min 57 s. La distance du
marathon est de 42,195 km. Calculer, avec 3 chiffres après la virgule,
sa vitesse moyenne en km /h.
2 h 2 min 57 s = 2 x3600 + 2 x60 +57s = 7377 s.
Vitesse = 42195 / 7377 =5,7198 m s-1 ou 5,7198 x3,6 = 20,591 km h-1.
2.a.
Sans pesanteur ? Calculer la force d'attraction de la terre sur un
astronaute en sortie à 500 km d'altitude en orbite autour de la terre.
Comparer à la valeur de cette force sur terre.
Masse de l'astronaute et de son équipement m = 150 kg.
Masse de la terre M = 5,97 1024 kg. Rayon terrestre R = 6370 km.
F = GmM /(R+h)2 = 6,67 10-11 x150 x5,97 1024 /((6370 +500) 103)2 =1265,5 N.
Poids au niveau du sol terrestre : m g = 150 x9,81 = 1471,5 N.
1471,5 /1265,5 ~1,16.
La force d'attraction au sol est 1,16 fois plus grande qu'à l'altitude de 500 km.
2.b. L'attraction
de la terre étant la seule force non négligeable s'exerçant sur
l'asttronaute, comment expliquer qu'il ne tombe pas comme un objet en
chute libre ? Discuter alors du titre de cet exercice ?
L'astronaute est relié au véhicule spatial, ce dernier possèdant une
vitesse non nulle dans le référentiel géocentrique.. Dans un
référentiel lié à ce véhicule, l'astronaute est soumis à une
force d'inertie centrifuge opposée à son poids. L'astronaute est en
situation d'apesanteur.
3. Chute libre On lance un caillou verticalement vers le haut avec une vitesse initiale de 10 m /s.
Quelle est l'altitude atteinte par ce caillou en considérant la main du lanceur à l'altitude zéro ?
En chute libre le caillou n'est soumis qu'à son poids.
La conservation de l'énergie mécanique conduit à h = v02 / (2g) = 100 / (2 x9,81) =5,097 ~5,1 m.
Quel temps s'écoule entre le lancer et la réception du caillou dans la main ?
Sur un axe vertical orienté vers le haut : v = -gt +v0.
Au point le plus haut, la vitesse est nulle.
Durée de la montée = durée de la descente = v0 / g =10 / 9,81 ~1,019 s.
2t = 2 x1,019 ~2,0 s.
Electricité.
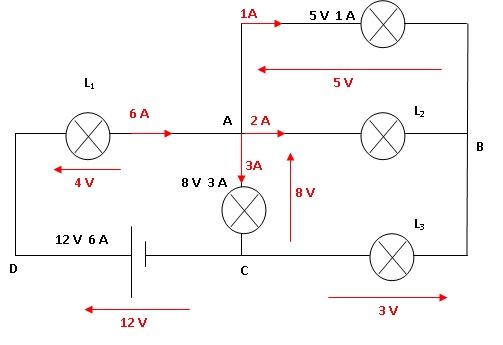
Les valeurs indiquées en noir sont les valeurs des tensions aux
bornes de dipoles concernés ainsi que celles des intensités traversant
ces dipoles.
|
|
|
1. Déterminer les tensions aux bornes des trois lampes L1, L2 et L3, ainsi que les intensités les traversant.
Loi des noeuds en A : l'intensité traversant L2 vaut 2 A.
Loi des noeuds en C : l'intensité traversant L3 vaut 3 A.
L1 est en série avec la pile ; l'intensité traversant L1 vaut 6 A.
Additivité des tensions :
UDC = UDA +UAC ; UDA = 12-8 = 4 V.
UAC = UAB +UBC ; UBC = 8-5 = 3 V.
2. Calculer les puissances électriques de chacun des dipoles. Indiquer si cette puissance est reçue ou fournie . Commenter.
Puissance fournie par la pile au circuit : 12 x 6 = 72 W.
Puissance reçue par la lampe L1 : 6 x4 =24 W.
Puissance reçue par la lampe L2 : 5 x 2 =10 W.
Puissance reçue par la lampe L3 : 3 x3 =9 W.
Puissance reçue par les autres lampes : 8 x3 = 24 W et 5 x1 = 5 W.
Puissance totale reçue par les lampes : 72 W = puissance fournie par la pile.
|
|
|
|
Energie et puissance.
1. Rappeler le lien entre puissance et énergie. Indiquer les unités utilisées.
Energie ( J) = Puissance (W) x temps ( s).
Energie ( Wh) = Puissance (W) x temps ( h).
2. On rappelle l'expression de l'énergie potentielle de pesanteur Epp = mgz où z est l'altitude.
Une pompe électrique remonte l'eau sur un dénivelé de 20 m et doit pomper 30 m3 par heure.
a. Calculer la puissance à fournir à l'eau pour la remonter ( on néglige la vitesse de l'eau dans les conduites ).
Débit : 30 / 3600 m3 s-1.
Masse d'eau remontée en une seconde : 30 / 3600 x1000 = 30 / 3,6 kg s-1.
Energie potentielle de cette masse d'eau : 30 / 3,6 x9,81 x20 =1635 J s-1 ou 1,635 kW.
b. Quel est le coût
minimal théorique de fonctionnement de la pompe pendant une journée
non-stop ? ( 1 kWh coûte environ 15 centimes d'euros. Que dire de ce
coût ?
1,635 x24 = 39,24 kWh ; coût : 39,24 x0,15 ~5,9 €, valeur très faible.
3. Une bouilloire électrique de 1500 W chauffe 0,5 L d'eau.
a. Calculer l'énergie thermique que doit engendrer la bouilloire pour amener l'eau de 15 °C à l'ébullition. Ceau = 4185 J kg-1 K-1.
Q=m Ceau Dq = 0,5 x4185 x(100-15) =177 862,5 J.
b. En déduire le temps qu'il faut pour chauffer l'eau. Que dire de ce temps ?
Energie (J) / puissance (W) = 177 862,5 / 1500 ~118,6 s ou environ 2 minutes.
|
|