QCM Mathématiques.
Concours Puissance 11, Fesic 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice1. Lecture graphique. A(0,4
; 3,6) ; B(3 ; 1) ; C(1 ; 1) ; D(1 ; 2) ; E(0 ; 2) ; F(1 ; 0) ; G(3 ; 3
) ; H(2 ; 1). Soient deux fonctions u et v définies sur l'intervalle [0
; 3] de courbes reorésentatives respectives C u et C v tracées ci-dessous.
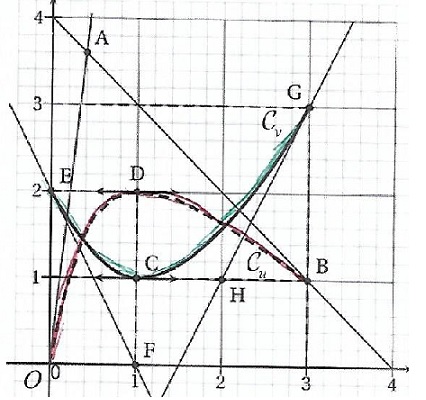
La droite (OA) est tangente à C u à l'origine du repère.
La droite (AB) est tangente à Cu au point B..
Les droites (EF) et (GH) sont tangentes à C v respectivement aux points E et G.
C u et C v admettent respectivement aux point D et C une tangente horizontale.
a. v'(3)=3. Faux.
Pente de la tangente à C v au point G : 2 / 1 = 2.
b. u'(0)= -9. Faux.
Pente de la tangente à Cu au point 0 : 3,6 /0,4 =9.
c. (1/v)'(1)= -v'(1). Faux.
v'(1) = 0 ; (1/v)' = -v' / v 2 ; (1/v')(1) = 0 /1=0.
d. (u x v)'(3)=1. Faux.
(u' v +v'u)(3) = -1 x 3 +2 x1 = -1.
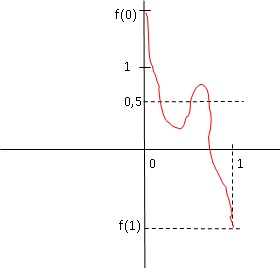
Exercice 2. Logique et fonctions Soit f une fonction définie et dérivable sur [0 ; 1]
a. f(0,5) est compris entre f(0) et f(1). Faux.
f peut présenter un extrémum sur cet intervalle.
b. Si f(0) >1 et f(1) <0 alors l'équation f(x) = 0,5 admet une unique solution dans l'intervalle [0 ; 1 ]. Faux.
Soit g une fonction définie sur l'intervalle [-2,5 ; 4,5 ] de courbe représentative Cg ci-dessous.
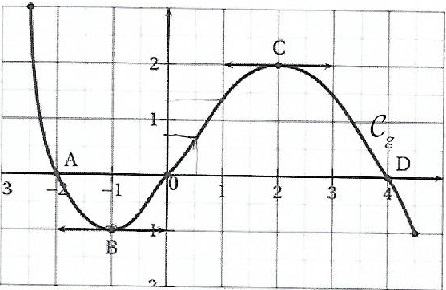
c. Si g(x)=0 alors x=4. Faux.
x=4 ; x = -2 ; x=0.
d. Si x appartient à {-1 ; 0 ; 2 ; 4 } alors g '(x) * g(x) =0. Vrai.
g'(-1) =0 ; g(0)=0 ; g'(2)=0 ; g(4)=0.
.
Exercice 3. Suites et algorithmes.
On définit la suite (un) par u0=0 et pour tout entier naturel n, un+1 = 0,5 (un2+12)½.
On pose (vn) la suite définie par vn = un2-4.
a. u1 = 3½ ; u2 = 0,5 x15½ ; u3 = 0,75 x7½. Vrai.
u1 = 0,5(0+12)½ =3½ ;
u2 = 0,5(3+12)½ =0,5 x15½ ;
u3 = 0,5(15/4+12)½ =63½/ 4=3/4 x7½ .
b. La suite (vn) est géométrique. Vrai.
vn+1 = un+12-4 =0,25( un2+12)-4=0,25 un2-1=0,25(un2-4) = 0,25 vn.
c. On démontre que, pour tout entier naturel n, un = [(4n-1) / 4n-1]½. Vrai.
Initialisation : la propriété est vraie au rang 0 et au rang 1.
Hérédité : on suppose la propriété vraie au rang p : up = [(4p-1) / 4p-1]½.
up+1 = 0,5 (up2+12)½=0,5[(4p-1) / 4p-1+12]½=0,5[(4p-1+12 x 4p-1)/ 4p-1]½;
(4p-1+12 x 4p-1)=(4p-1+12/4 x 4p)=(4p-1+3 x 4p)=4p+1-1.
up+1 = 0,5[(4p+1-1) / 4p-1]½=[(4p+1-1) / 4p-1]½/2 =[(4p+1-1) / 4p]½. La propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 0 et héréditaire, elle est vrai pour tout n.
On considère l'algorithme suivant :

d. Si E =0,1, N = 2. Vrai.
N
|
0
|
1
|
2
|
U
|
0
|
3½
|
15½/2
|
2-U >0,1
|
vrai
|
vrai
|
faux
|
Exercice 4. Limites et asymptotes.
a. Quand x tend vers l'infini, la limite de ln[(3x+1) / (x2-3)] est moins l'infini. Vrai.
(3x+1) / (x2-3) tend vers zéro quand x tend vers l'infini.
Le logaritme d'un nombre qu tend vers zéro est égal à moins l'infini.
b. Quand x tend vers plus l'infini, la limite de 2/3x ex est moins l'infini. Faux.
ex tend vers l'infini ; x tend vers linfini.
Quand x tend vers plus l'infini, la limite de 2/3x ex est plus l'infini.
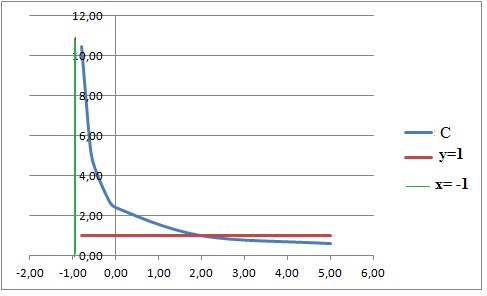
Soit f la fonction définie sur ]-1 ; +oo[ par f(x) =((x+2)½+1] / (x+1) de courbe représentative C dans un repère orthonormé.
c. C admet la droite d'équation y=1comme asymptotoe horizontale en +oo. Faux.
d. C admet comme asymptote verticale la droite d'équation x=-1. Vrai.
|
....
.....
|
Exercice 5. Calcul d'intégrale.
Exercice 6. Etude de 2 fonctions.
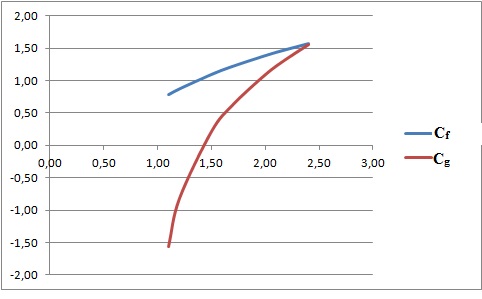
Soient f et g deux fonctions définies par f(x) = ln(2x) et g(x) = ln(x2-1) de courbes représentative respectives Cf et Cg.
a. g(0,5) <0.
Faux.
g (x) n'est pas définie sur ]-1 ; +1 [
b.
g'(x) =1/(x2-1) Faux.
On pose u = x2-1 ; u' = 2x ; g'(x) = u' / u = 2x /(x2-1).
c.
La tangente à Cg en x = 2½ a pour équation y = 2 x2½x-4. Vrai.
g'(2½)=2 x2½; la tangente passe au point de coordonnées ( 2½ ; 0) ;
équation de la tangente : y = 2 x2½x +b ; 0 = 4+b ; b = -4.
d. Si x appartient à ]1 ; 1+2½], la courbe Cg est au dessus de Cf. Faux.
 |
|
|
Exercice
7. Etude d'une fonction exponentielle.
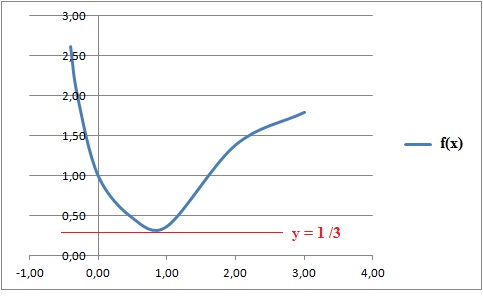
Soit fla fonction définie sur R par f(x) = exp(x2-2x).
a. f(1) =-1/e. Faux.
f(1) = exp(12-2) = e-1 = 1 /e.
b.
La limite de f(x) en moins l'infini est égale à la limite de f(x) en plus l'infini. Vrai.
c.f '(x) = f(x). Faux.
f '(x) = (2x-2) exp(x2-2x).
d. L'équation f(x) = 1 /3 admet deux solutions dans R. Faux.
ln(1/3) = -ln3 = x2-2x ; x2-2x +ln 3 = 0 ; D = 4-4 ln3 <0.
Exercice 8. Notions de base sur les complexes.
Le point A a pour affixe zA = 1+i. Soit C le cercle de centre O passant par A.
Soit B un point de C d'affixe zB positive
On définit le point E tel que le quadrilatère OBEA soit un losange.
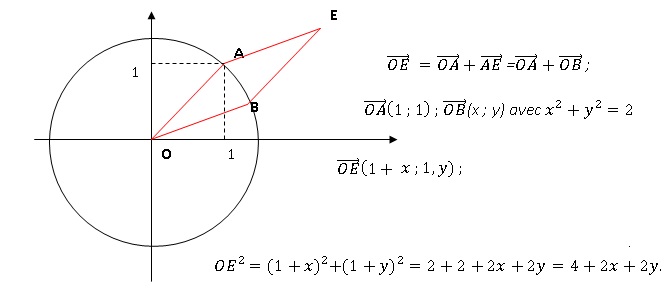
a. zA = exp(ip/4). Faux.
Module de zA : (12+12)½=2½ ; zA =2½ exp(ip/4).
b. zB = 1,5. Faux.
Le point B appartient au cercle ; son module vaut 2½.
c. zE = (1+2½)+i. Faux.
d. OE = 2 x2½. Faux.
|
|
|
|
Exercice
9. Probabilité.
Une
fois sur 10 quand je prends mon vélo au moins l'une des deux roues est
crevée ; la probabilité que la roue avant soit crevée est 0,05 et
les crevaisons de la roue avant et de la roue arrière sont
indépendantes.
On note V l'événement " la roue avant est crevée" et R l'événement " la roue arrière est crevée".
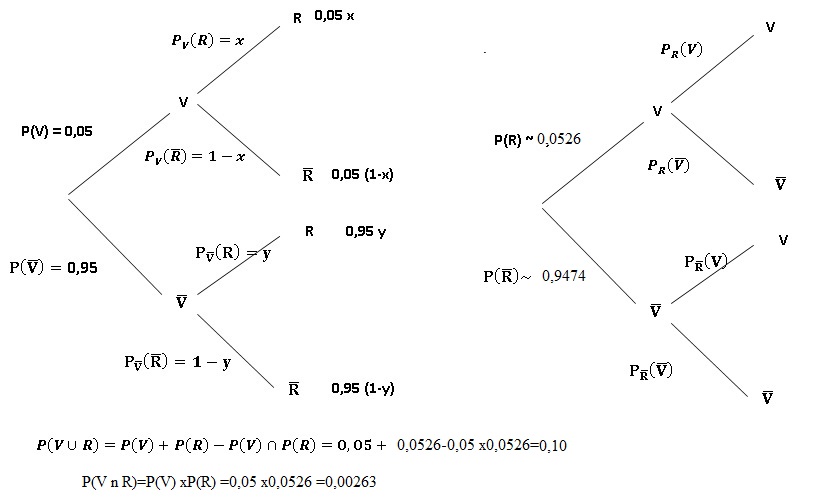
a. P(V U R) =0,1 et P (V n R)=0,05 xP(R). Vrai.
b. J'ai constaté que la roue arrière était crevée ; la probabilité que la roue avant le soit également vaut 0,05. Vrai.
P(V n R) / P(R) = 0,25 / 95 x 95 /5 = 0,05.
c. La roue avant et la roue arrière ont la même probabilité d'être crevées. Faux.
Probabilité qu'au moins une roue soit crevée :
0,05 +0,95 y = 0,10 ; y = 5 / 95 ~ 0,0526.
d. Il y a une chance sur 380 pour que les deux roures soient crevées. Vrai.
0,05 *5 / 95 =0,25 / 95 = 1 / 380.
Exercice 10. Probabilités continues.
Soient µ1 et µ2 deux nombres réels, s1 et s2 deux réels positifs.Sur le graphe ci-dessous on a représentées Cf1 et Cf2 respectivement les courbes représentatives des fonctions de densité f1 et f2 de deux lois normales N1(µ1; s21) et N2(µ2; s22).
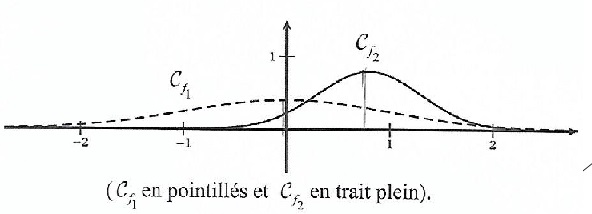
a. µ1 <µ2 et s1 < s2. Faux.
Plus la courbe est plate, plus l'écart type est grand.
Soit l1 et l2 deux nombres réels positifs. Sur le graphe ci-dessous ont été représentées Cg1 et Cg2 respectivement les courbes représentatives des fonctions de densité g1 et g2 de deux lois exponentielles de paramètres respectifs l1 et l2.
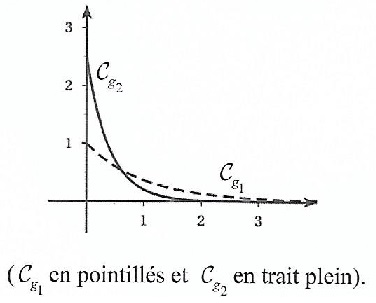
b. l1 < l2. Vrai.
Dans
une région agricole, le rendement des parcelles de blé peut être
assimilé à une variable aléatoire suivant la loi normale d'espérance
100 et d'écart-type 8 ( en quintaux par hectare).
c. La variable aléatoire Z = (R-100) / 82 suit la loi normale centré réduite. Faux.
(R-100) / 8 suit la loi normale centré réduite.
d. La probabilité que la parcelle ait un rendement inférieur à 116 quintaux par hectare est égale à 0,9. Faux
Y = (116-100) / 8 =2. ; Y suit la loi normale centrée réduite.
Les tables donnent P(Y<2)=0,977.
Exercice11. Notions de base dans l'espace.
On considère deux plans (P) et (Q) d'équations cartésiennes respectives (P) : x-y=0 et (Q) : y+2z-3=0.
Ces plans se coupent suivant une droite (D) et on pose K le point de coordonnées K(1 ; 0 ; 2).
a. (P) et (Q sont deux plans orthogonaux. Faux.
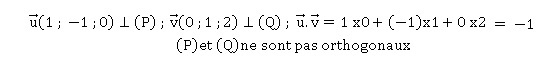
b. Le vecteur de coordonnées (2 ; 2 ; -1) est un vecteur directeur de la droite (D). Vrai.
Un vecteur directeur de la droite (D) de représentation paramétrique x=t ; y =t ; z = (3-t) / 2 a pour coordonnées ( 1 ; 1 ; -0,5) ou encore (2 ; 2 ; -1).
c. x=t ; y=t ; z = (3-t) / 2 avec t réel est une représentation paramétrique de la droite (D). Vrai.
Si (D) appartient au plan (P) : t-t=0 est vérifié.
Si (D) appartient au plan (Q) : t+3-t -3 =0 est vérifié.
d. Le plan (R) d'équation cartésienne 2x+2y-z = 0 est parallèle à (D) et contient la droite OK. Faux.

Exercice 12. Complexes et géométrie.
Soit (E) l'équation z2-6z+12=0.
a. (E) admet deux solutions complexes z1 et z2. Vrai.
Discriminant : (-6)2 -4 x12= -12 = 12 i2.
z1 =(6+2 i x3½) / 2 = 3+i x3½. z2 =(6-2 i x3½) / 2 = 3-i x3½.
Le discriminant étant négatif, (E) admet deux solutions complexes.
On pose z1 la solution ayant une partie imaginaire positive.
b.4-z1 = 2 exp(2ip/3). Faux.
4-z1 =1-i x3½. Module de 4-z1 : ( 12 +3)½ =2.
(4-z1 ) /2 = 0,5 -i x3½ / 2 =sin(5p/6) + i cos(5p/6) =exp(5 i p /6).
Soit A le point d'affixe zA = 4 et M1 et M2 les points d'affixes respectives z1 et z2.
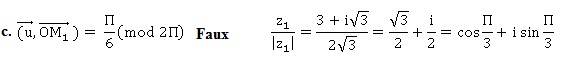
d. Le point M1 est situé sur le cercle de diamètre [OA]. Vrai.
Equation de ce cercle centré au point de coordonnées (2 ; 0) : (x-2)2 +y2 = 4
Si M1( 3 ;3½ ) appartient à ce cercle : (3-2)2 +(3½)2 = 1+3=4.
|
|
Exercice 13. Trigonométrie dans l'escargot.
Dans le triangle OA0B0, isocèle en O, A1 est le milieu du segment [A0B0]. On note B1 le symétrique de A1 par rapport à la droite (OB0) et A2 le milieu du segment [A1B1]. En réitérant le processus on obtient, pour tout entier naturel n, une suite de triangles isocèles OAnBn.
a. OAn+1 = sin a x OAn et AnAn+1 = cos a xOAn, pour tout entier n. Faux.
sin a = AnAn+1 / OAn et cos a =OAn+1 / / OAn .
b. Pour tout entier n, on a OAn = l x (cos a)n. Vrai.
Initialisation : OA1 = l cos a ; la propriété est vraie au rang 1.
Hérédité : on suppose vraie OAp = l (cos a )p.
OAp+1 = OAp cos a = l (cos a )p+1. la propriété est vraie au rang p+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, donc la propriété est vrai pour tout n entier.
On pose pour tout entier naturel n non nul, la suite (Ln) définie par Ln = A0A1 +A1A2 +...+An-1An.
c. Ln= l x sin a (1-(cos a)n+1) / (1-cos a). Faux.
Suite géométrique de raison cos a.
A0A1 +A1A2 +...+An-1An = l x sin a + l x sin a xcos a +.....+ l x sin a x(cos a)n-1 = l x sin a [1-( cos a )n] / (1-cos a).
d. Ln= l x (1-(cos a)n) / tan( a/2). Vrai.
sin a = 2 sin (a/2) cos (a/2) ; (1-cos a) = 2 sin2(a/2) ; sin a / (1-cos a)=cos (a/2) / sin (a/2) = 1 /tan(a/2).
Exercice 14. Fonction dépendant d'un paramètre.
Pour tout nombre réel k >0, on définit la fonction fk(x) = (x+k)e-x de courbe représentative Ck.
a. Ck coupe les axes du repère aux points de coordonnées (k ; 0) et (0 ; k). Faux.
(x+k) e-x=0 ; x = -k ; point de coordonnées ( -k ; 0).
(0+k) e0 =k ; point de coordonnées ( 0 ; k).
b. Si k = 3 alors la fonction f3 admet e2 comme minimum sur R. Faux.
f3 =(x+3)e-x. f3' = e-x -(x+3)e-x = -(x+2)e-x ; la dérivée s'annule pour x = -2.
La dérivée est positive si x <-2 ( fonction croissante) et négative si x >-2 ( fonction décroissante).
Il s'agit d'un maximum.
c. La fonction Fk définie par Fk = (-x-1-k) e-x est une primitive de fk. Vrai.
Fk' =-e-x- (-x-1-k) e-x =(x+k)e-x=fk.
d. L'aire de la portion de plan délimitée par la courbe C3, l'axe des abscisses et les droites d'équation x=0 et x=1 est égale à 4-5e-1. Vrai.
A = [(-x-1-3)e-x]01 =-5e-1+4.
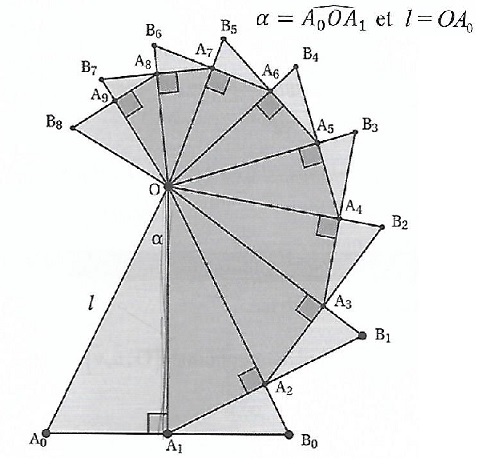
Exercice 15. Notion d'espace dans un cube de côté égal à1.
a. Le volume du tétraèdre BCDG est égal à 1 /6. Vrai.
Aire de la base BCD x hauteur CG / 3 = 0,5 x1 /3 = 1 /6.
b. L'aire du triangle BDG est égale à 3½/4. Faux.
Base BD = BG= 2½ ; hauteur : GK2 = 0,5 +2 =2,5.
Aire BDG = 2½ x2,5½ /2 = 5½ /2.
c. La distance du point C au plan (BDG) est égale à 2 / 3½. Vrai.
d = |-yC -1| / (12+(-1)2+12)½=2 / 3½.
d. Une équation cartésienne du plan(BDG) est : x +y -z-1=0. Vrai.
B (1 ; 0 ; 0) appartient à ce plan d'équation cartésienne ax+by+cz+d=0. a+d = 0 soit d = -a.
D (0 ; 1 ; 0) appartient à ce plan d'équation cartésienne ax+by+cz+d=0. b+d = 0 soit b=-d = a.
G (1 ; 1 ; 1) appartient à ce plan d'équation cartésienne ax+ay+cz-a=0. a+ a+c -a= 0 soit c=- a.
Equation cartésienne de ce plan : ax +ay -az -a =0.
Exercice 16. Etude d'une spirale.
D1 et D2 sont deux droites d'équation respective y=-x et=x et M0(2 ; 0).
On construit M1 le projeté orthogonal de M0 sur la droite D2, M2 le projeté orthogonal de M1 sur l'axe des ordonnées, M3 le projeté orthogonal de M2 sur la droite D1 et M4 le projeté orthogonal de M3 sur l'axe des abscisses.
On réitère le même procédé afin de définir, pour tout entier naturel n, la suite de points(Mn).
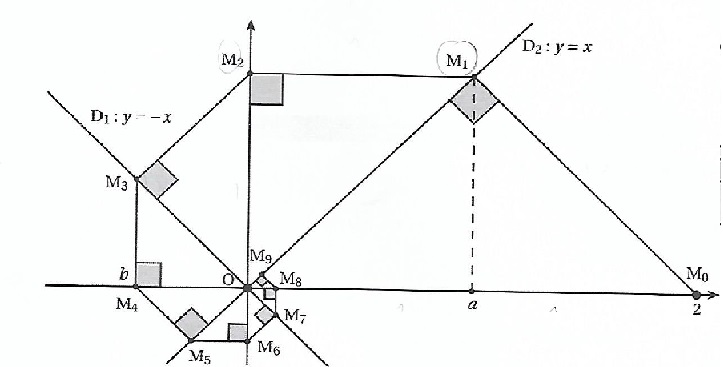
On note a l'abscisse du point M1 et b l'abscisse du point M4 avec a et b deux nombres réels.
a. a=1 et M1M2=1. Vrai.
b. M2M3 = 3½ / 2. Faux.
M2M3 =(0,52 +0,52)½ =1 / 2½ = M1M2 / 2½.
Pour tout entier naturel n, on définit les suites (Ln) et (Sn) à l'aide des relations ln = MnMn+1 et Sn = Slk.
c. ln+1=ln / 2½. Vrai.
Le côté du carré est égal à la diagonale divisée par 2½.
d. Quand n tend vers l'infini, Sn tend vers 2 x 2½+1. Faux.
Sn = M0M1 +M1M2 +...+MnMn+1= 2½ (1+1 /2½ +.....+1/(2½)n)= 2½ (1-(1/2½)n+1) /(1-1/2½).
Quand n tend vers l'infini : (1/2½)n+1 tend vers zéro et Sn tend vers 2½ /(1-1/2½)=2 /(2½-1) =2(2½+1).
|
|