Mathématiques, Probabilités
Bts groupe D 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie A. Défauts de fabrication
Un verre à pied est constitué de deux parties : le calice (ou bol) et
le pied. Ces deux parties sont assemblées à chaud et fabriquées par
deux procédés différents.
Elles peuvent présenter des défauts indépendamment l’une de l’autre.
On a constaté que la machine qui fabrique les calices produit 5% de
calices défectueux et que la machine qui fabrique les pieds produit 2%
de pieds défectueux.
On appelle A l’évènement « le calice est défectueux »et B l’évènement «
le pied est défectueux ». On prélève un verre au hasard dans la
production.
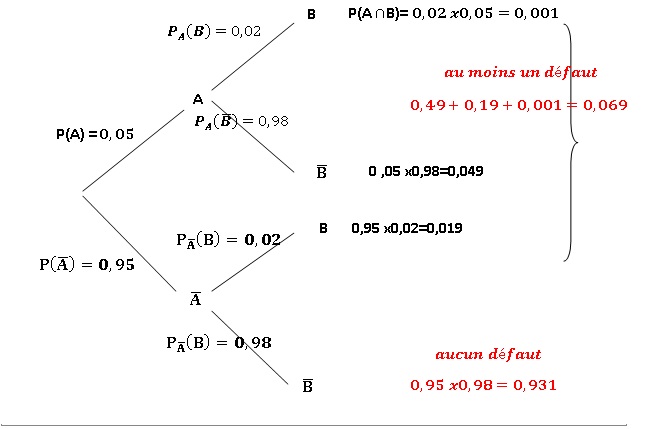
1. Calculer la probabilité pour que le verre ait les deux défauts.
P(A n B)=0,05 x0,02 = 0,001.
2. Calculer la probabilité pour que le verre soit défectueux c’est-à dire que le verre ait au moins un
des deux défauts.
|
....
.....
|
Partie B : Vérification d’un lot
Dans un stock important de verres à pied, on en prélève 20 au hasard pour vérification.
Le stock est assez important pour qu’on puisse assimiler ce prélèvement
à un tirage avec remise de 20 verres. On considère la variable
aléatoire X qui à tout prélèvement de 20 verres associe le nombre de
verres défectueux. On suppose que la probabilité qu’un verre soit
défectueux est de p = 0,069.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 20. La
probabilité qu'un verre soit non conforme est constante p = 0,069.
La loi binomiale B(n=20, p = 0,069) est valide.
2. Calculer à 10−2 près la probabilité de l’évènement « dans un tel prélèvement cinq verres au moins sont défectueux ».
P(X > 5) =1- P(X <5) =1-0,9982 ~0,00179 ~0,002.
Partie C. Diamètre du buvant du verre
Dans cette question on s’intéresse au diamètre, exprimé en millimètre, d’ouverture du verre appelée « buvant » du verre.
On note D la variable aléatoire qui à chaque verre associe le diamètre
de son « buvant ». On admet que D suit la loi normale de paramètres m =
46 et s = 0,3.
On prélève au hasard un verre dans la production.
1. Calculer à 10−2 près la probabilité que le diamètre de ce verre soit compris entre 45,8 et 46,3.
P (45,8 < D < 46,3) = P(x < 46,3) -P(X < 45,8) =0,8413-0,2525 =0,589 ~0,59.
2. Déterminer. par la méthode de votre choix, une valeur approchée à 10−1 nombre réel a tel que P(46−a < D < 46+a) = 0,95.
a = 1,96 s =1,96 x0,3=0,588 ~0,6.
|
|
|
Partie D. Brillance des verres
La brillance des verres est contrôlée par un dispositif électronique
qui analyse les reflets du verre. La durée de bon fonctionnement de ce
dispositif, exprimée en mois, est modélisée par une variable aléatoire
T qui suit une loi exponentielle de paramètre l >0.
1. Montrer que P(T < t ) = 1−e−lt .
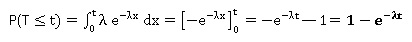
2. Sachant que P(T < 24) = 0,93, montrer que la valeur arrondie au centième de l est 0,11.
0,93 = 1 -exp(-24 l) ;
exp(-24 l) = 0,07 ;
-24 l = ln(0,07) ;
l = ln(0,07) / (-24) ~0,11.
3. Quelle est l’espérance de la durée de bon fonctionnement de ce dispositif ?
On arrondira à l’unité et on interprétera le résultat.
1 / l = 1 / 0,11 ~9,0.
En moyenne,le dipositif fonctionne correctement pendant 9 mois.
4. La probabilité que la durée de vie soit supérieure à 4 ans est-elle supérieure à 1%?
Justifier.
P(D > 48) =exp(-0,11 x48) = 0,0051 ( ~0,5 %).
Réponse : non.
|
|