Fonction, équation
différentielle.
BTS groupe C 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Antilles Métropole.
En sylviculture, le cubage des arbres est uneactivité essentielle qui
consiste à chiffrer régulièrement des volumes de bois, qu’ils soient
abattus ou encore sur pied.
Afin d’éviter toute contestation entre les différents acteurs du
secteur, exploitants et négociants, le cubage des bois est régi par les
normes AFNOR NF B 53−020 et NF B 53−017.
En fonction de leur destination, on distingue plusieurs types de bois,
parmi lesquels:
- Le bois d’oeuvre (BO), partie du tronc dont le diamètre est supérieur
à 20 cm, destinée, en fonction de l’essence, à la construction
(charpente, bardage), la menuiserie ou l’ébénisterie.
- Le bois fort (BF), partie de l’arbre (tronc et branches) dont le
diamètre est supérieur à 7 cm.
Le bois fort est donc le bois d’oeuvre auquel s’ajoute toute une partie
de l’arbre valorisable
dans l’industrie (trituration, papeterie, chauffage, . . . ).
On s’intéressera, dans la suite, uniquement à l’étude du bois fort.
Le but de l’exercice est d’anticiper la croissance d’un plant de
Douglas (une des deux
essences d’arbre les plus cultivées en France pour ses remarquables
propriétés mécaniques).
Les arbres étudiés dans cet exercice ont dix ans ou plus.
Partie 1 :Modèle
statistique.
Le tableau suivant donne le volume de bois fort, en m3, d’un
plant de Douglas, en fonction de son âge, exprimé en années :
t
( années)
|
10
|
20
|
30
|
50
|
V
(m3)
|
0,09
|
0,19
|
0,51
|
2,11
|
Q=ln(7/V
-1)
|
4,34
|
3,58
|
2,54
|
0,84
|
Une première méthode pour
anticiper la croissance de ce plant de Douglas consiste à étudier le
coefficient Q = ln( 7 / V −1)¶.
1. Compléter ce
tableau (arrondir à 10−2 près).
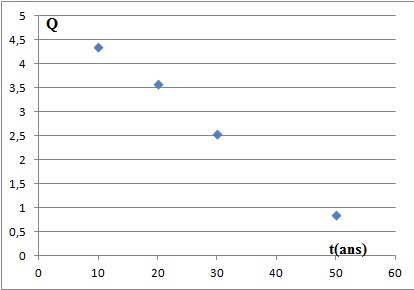
2. Représenter le
nuage de points de la série statistique constituée des deux variables t
et Q.
3. On s’intéresse à
l’ajustement affine de Q en t par la méthode des moindres carrés.
On obtient sur l’écran d’une calculatrice :
a = -0,088616 ; b = 5,2629789 ; r =-0,9990631 ; y=ax+b.
Donner une équation de la droite d’ajustement de Q en t par la méthode
des moindres carrés (on arrondira les coefficients à 10−3
près).
y = -0,0886 x +5,263.
4. Déterminer, en
utilisant cet ajustement, la valeur prévisible de Q lorsque t = 80.
Q = -0,0886 x 80 +5,263 = -1,825 ~-1,83.
5. Quel volume de
bois fort peut-on espérer tirer de ce plant de Douglas lorsqu’il aura
80 ans ?
ln(7 /V-1) = -1,825 ; 7 /V =1 +e-1,825 =1,161 ; V = 7 /1,161
= 6,03 m3.
Partie 2 :Modèle dynamique.
Une autre approche de l’étude de la croissance d’un arbre, c’est-à-dire
de son volume de bois fort, consiste à déterminer d’abord la fonction f
définie par f (t )= 1 /V (t )
où V (t ) désigne le volume de bois fort pour un arbre âgé de t années.
Dans la suite de l’exercice, on s’intéresse aux valeurs de t
supérieures ou égales à 10.
Dans cette modélisation, on admet que cette fonction f est une solution
particulière d’une équation différentielle de la forme : y′ +0,088y = b.
Dans cette équation, y désigne une fonction définie et dérivable sur
[10 ; +∞[.
0,088 est un coefficient adapté à tous les Douglas et b est un réel qui
dépend de la qualité du plant étudié et des conditions de culture.
Dans toute la suite, on considère le plant de Douglas étudié dans la
partie 1, dont le volume de bois fort est donné par le premier tableau
de la partie 1.
1. L’utilisation
d’un logiciel a permis de représenter les volumes de bois fort en
fonction du temps t pour différents plants de Douglas, c’est-à-dire
pour différentes valeurs du réel b.
Parmi les courbes données, l’une d’entre elles représente le volume V
de bois fort du plant de Douglas étudié. Expliquer pourquoi on peut
choisir 0,012 comme valeur de b pour ce plant
de Douglas.
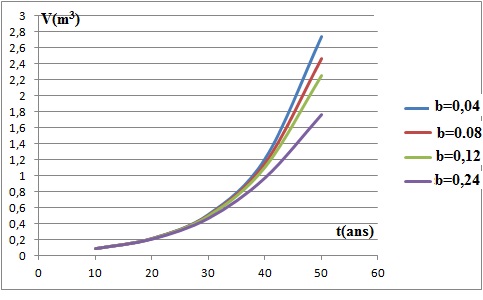
A t = 50 ans, V ~2,1 m3 ( courbe verte).
2. On appelle (E)
l’équation différentielle : y′ +0,088y = 0,012.
a. Déterminer
l’ensemble des solutions de l’équation différentielle (E0) :
y′ +0,088y = 0.
y = A exp(-0,088t)
avec A une constante.
.b. Démontrer que la fonction
constante g , définie sur [10 ; +∞[ par g (t ) =0,012 / 0,088
est une solution particulière de l’équation différentielle (E).
g'(t) = 0 ; repport dans (E) : 0,088 g(t) = 0,012 ; g(t) = 0,012 /
0,088.
c. En déduire
l’ensemble des solutions de l’équation différentielle (E).
f(t) = A
exp(-0,088t) +0,012 /0,088.
d. Calculer f (10) puis déterminer
la solution particulière f de cette équation (E) concernant le plant de
Douglas étudié.
f(10) = 1 / V = 1 /0,09 ~11,1 m-3.
f(10)=A exp(-0,88) +0,012 /0,088=11,1.
0,4148 A +0,1364 = 11,1 ; A =26,46.
f(t) = 26,46 exp(-0,088t) +0,012 /0,088.
|
|
|
3. Dans cette question, on admet que
le volume de bois fort du plant deDouglas
étudié est défini par l’expression :
V (t )=1/(26,46e−0,088t +0,14) où t désigne le temps en
années.
a. Quel volume de bois fort peut-on
espérer de ce plant de Douglas quand il aura 80 ans ?
V =1 /(26,46 e-0,088 x80) +0,14) =6,128 ~6,13 m3.
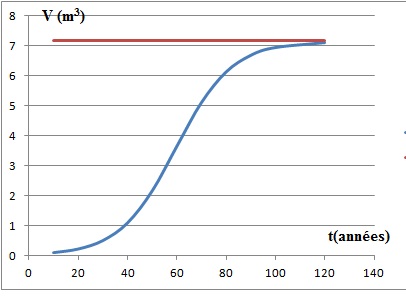
b. Expliquer
pourquoi la courbe représentative de la fonction V admet une asymptote
horizontale et en donner une équation.
Quand t tend vers l'infini, le terme e−0,088t
tend vers zéro ; par suite V(t) tend vers 1 /0,14 ~ 7,14 m3.
c. Tracer cette asymptote sur le
graphique donné et compléter la courbe représentative de la fonction
V.L’étude des variations de la fonction V n’est pas attendue.
4. L’OfficeNational
des Forêts conseille aux sylviculteurs de commercialiser leurs Douglas
lorsqu’ils ont atteint 85% de la valeur limite du volume de bois fort.
À quel âge est-il conseillé de commercialiser le plant de Douglas
étudié ?
0,85 x7,14 = 6,07 m3.
1 / 6,07 = 0,1647 = 26,46e−0,088t
+0,14.
e−0,088t =(0,1647-0,14) /
26,46=9,337 10-4.
t
=- ln(9,337 10-4) / 0,088 =79,27 ~79 ans.
|
|