Production de la
bière,
bac
SPCL métropole 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Partie 1 – Dosage conductimétrique des ions
chlorure dans une eau de brassage (7 points)
1.1. Citer les
matières premières utilisées dans la fabrication de la bière.
Malt, houblon, eau et levures.
En brasserie, les bières sont toutes produites selon le même procédé.
Cependant, en fonction
notamment de l’eau utilisée pour le brassage, toutes ne possèdent pas
les mêmes caractéristiques
(goût, aspect, etc...).
Afin de savoir si l’eau utilisée pour le brassage convient pour une
production de bière brune, il faut doser les ions chlorure. Pour ce
faire, on procède à un titrage par une solution de nitrate d’argent
(Ag +(aq) + NO 3-(aq)). Le dosage est
suivi par conductimétrie. L’équation de la réaction de dosage est la
suivante :
Ag +(aq) + Cl -(aq) --> AgCl(s)
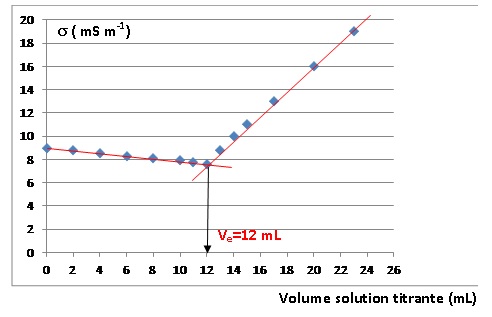
1.2. En s’aidant
des valeurs de conductivités ioniques molaires données , justifier
l’allure de la courbe de dosage. Montrer ensuite graphiquement
que le volume équivalent V e vaut 12,0 mL.
l(Ag +)=6,19
mS mol -1 m 2 ; l(Cl-)=7,639
mS mol-1 m2 ; l(NO3-)=7,15
mS mol-1 m2 .
Avant
l'équivalence, Ag+
est en défaut : du point de vue de la conductimétrie, tout se passe
comme si on remplaçait des ions chlorure par des ions nitrate, de
conductivité molaire ionique moindre. La conductivité de la solution
décroît.
Après
l'équivalence, Ag+ est en excès : on ajoute des ions
argent et des ions nitrate à la solution, sa conductivité croît.
1.3. Calcul
de la concentration massique en ions chlorure.
1.3.1. Déterminer
la valeur de la concentration molaire en ions chlorure C Cl-
de l’eau de
brassage. V 1 = 100 ±1 mL ; C Ag+ = 10,0 ±0,1 mmol L -1.
A l'équivalence
:CCl- V1 = CAg+ Ve ; CCl-
= CAg+ Ve / V1= 10,0 x12
/100 =1,2 mmol L-1.
1.3.2. La masse
molaire atomique du chlore vaut M = 35,5 g.mol -1. Montrer
que la
concentration massique en ions chlorure C M vaut 42,6 mg.L -1.
C M = C Cl- M = 1,2 x35,5 = 42,6 mg L-1.
1.4. On cherche à estimer
l’incertitude sur la concentration massique en ions chlorure U(CM)
dans l’eau de brassage.
1.4.1.
L’incertitude U(V1) sur le volume de l’eau de brassage V1
est de 1 mL.
On estime que l’incertitude U(Ve) sur la détermination du
volume équivalent Ve vaut 0,5 mL.
On admet que la relation de propagation des incertitudes s’écrit :
U(CM) = CM×[(U(V1) / V1)2+(U(Ve)
/ Ve)2 +(U(CAg+) / CAg+)2]½.
Comparer l’influence des différentes sources d’erreur sur l’estimation
de U(CM) et
justifier qu’une d’entre elles est prépondérante devant les autres.
U(V1)
/ V1=1 /100 = 0,01 ; U(Ve) / Ve=0,5
/12~0,042 ; U(CAg+) / CAg+=0,1
/ 10 = 0,01.
U(Ve) / Ve
est quatre fois plus grande que les autres.
1.4.2. En ne tenant compte que de la
source d’erreur prépondérante, calculer U(CM) puis
écrire correctement la concentration massique en ions chlorure de l’eau
de brassage CM avec son incertitude.
U(CM) = 42,6×[(10-2)2+(4,2
10-2)2 +(10-2)2]½=42,6
x0,044 ~2 mg L-1.
CM =
43 ±2 mg L-1.
1.5. Déterminer si cette eau
convient pour la fabrication d’une bière brune.
L'eau doit contenir entre 100 et 200 mg L-1 d'ion chlorure.
43 est en dehors de cet intervalle. Cette eau ne convient pas à la
fabrication de bière brune.
|
....
.....
|
Partie 2 – Autour de la fermentation
(8 points)
La fermentation du moût est un processus exothermique. Elle nécessite
une température optimale
de 9,0 °C, or le moût sort de la dernière cuve de brassage à 100,0 °C.
Pour assurer une bonne
fermentation, il est donc nécessaire de :
- refroidir le moût de 100,0 °C à 9,0 °C. La rapidité du
refroidissement est cruciale afin d’éviter l’infection par
d’éventuelles bactéries. On utilise pour cela un échangeur à plaques.
- maintenir le contenu de la cuve à 9,0 °C durant toute la fermentation
à l’aide d’un système
frigorifique.
A – Le
refroidissement du moût
L’échangeur est alimenté par de l’eau froide ; il en ressort de l’eau
tiède qui pourra être réutilisée
dans une autre partie de l’usine. Le débit volumique d’eau froide DV
peut être modifié avec une
vanne commandée par un régulateur, en lien avec le capteur de
température placé à la sortie de
l’échangeur.
2.1. L’eau et le
moût circulent à contre-courant dans l’échangeur. Justifier ce choix.
Dans l'échangeur à plaques, la circulation à contre-courant
permet un meilleur échange thermique entre les deux liquides.
2.2. Le
fonctionnement de l’échangeur est régi par un régulateur.
Indiquer la grandeur réglée, la grandeur réglante et la valeur de la
consigne.
La grandeur réglée est la température de sortie du moût ; la grandeur
réglante est le débit volumique d'eau froide ; la valeur de consigne
est 9°C.
B – Maintien en
température de la cuve de fermentation.
Durant toute la fermentation (une semaine), la température intérieure
de la cuve doit être
maintenue à 9,0 °C. Pour ce faire, un système frigorifique est installé
sur la cuve de fermentation.
Ce système permet par ailleurs de réchauffer de l’eau stockée dans un
bassin. Cette eau sera
ultérieurement utilisée comme eau de brassage.
La température de la pièce dans laquelle se trouve la cuve est de 21 °C.
2.3. Nécessité d’un
système de refroidissement
2.3.1. Montrer que
le flux thermique F
traversant la paroi de la cuve est de l’ordre de 430 W.
F = ( qc-qf) / R avec R =
2,810-2 °C W-1.
F =
(21-9) / (2,8 10-2) =428,57 ~430 W.
2.3.2. En vous
appuyant sur vos connaissances et en le justifiant, préciser le sens du
transfert thermique à travers la paroi de la cuve. Justifier la
nécessité d’un système de refroidissement.
Le transfert thermique s'effectue de la pièce ( source chaude ) vers le
moût ( source froide). Sans refroidissement la température du moût va
croître pour atteindre 21°C.
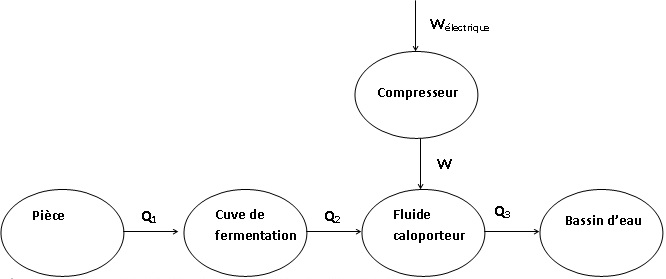
2.4. Compléter le
schéma énergétique du système en sélectionnant certaines expressions
parmi celles proposées dans la liste suivante :
bassin d’eau ; compresseur ; cuve de fermentation ;
détendeur ; pièce ; fluide caloporteur.
Préciser à l’aide de flèches le sens réel des transferts énergétiques
notés Q pour des transferts thermiques, et W pour du travail.
2.5. Évaluation du
coût hebdomadaire du maintien en température de la cuve en négligeant
l’énergie thermique libérée par la réaction de fermentation
2.5.1. Déduire de
la question 2.3.1. la quantité d’énergie thermique Q1
apportée au contenu de la cuve pendant 1,0 s par le milieu extérieur.
Q1 = 430 J.
2.5.2. On note Q2
l’énergie thermique cédée par la cuve de fermentation au fluide
caloporteur. Sachant que la température intérieure de la cuve doit être
constante, établir un lien entre les valeurs absolues des énergies
thermiques |Q1| et |Q2|. Justifier la réponse.
Pour une température constante du moût : l'énergie reçue par la cuve
doit être éliminée par le fluide caloporteur. |Q1| = |Q2|.
2.5.3. Exprimer l’efficacité
énergétique frigorifique EEF en fonction des notations utilisées dans
le schéma ci-dessus.
EEF = énergie échangée enntre la source froide et le fluide
calopoerteur / énergie électrique consommée par la machine.
EEF = |Q2| /
Wélectrique.
Vérifier que l’énergie électrique consommée par la machine pour
maintenir l’intérieur de la cuve à 9,0 °C pendant 1,0 s est de l’ordre
de 200 J.
EEF = 2,1 = |Q2| / Wélectrique
= 430 / Wélectrique .
Wélectrique =430
/ 2,1 ~200 J.
2.5.4.
Calculer l’énergie nécessaire au maintien en température de la cuve
pendant une durée d’une semaine, soit 7 jours (durée de la première
étape de fermentation).
Sachant que l’on peut estimer le coût de 1 kW.h d’électricité à 0,145
€, calculer le coût financier du maintien de la cuve à 9,0 °C pendant 7
jours.
7 jours = 7 x24 *3600 = 6,048 105 s.
Energie = 6,048 105 x 200 = 1,21 108 J ou 1,21 108
/(3,6 106)=33,6 kWh.
Coût : 33,6 x 0,145 = 4,87 €.
2.5.5. En tenant
compte de la réaction de fermentation qui a lieu à l’intérieur de cette
cuve,
discuter de la validité de l’estimation du coût financier du maintien
de la cuve à 9,0 °C effectuée précédemment.
La fermentation est exothermique. Le fluide caloporteur doit évacuer
d'avantage d'énergie. Le coût réel est sous estimé.
|
|
|
Partie
3 – Le conditionnement de la bière (5 points)
On s’intéresse dans cette partie à la mise en bouteille de la bière. Le
système retenu pour
contrôler le niveau de bière au remplissage de chaque bouteille est
constitué d’une fibre optique
dont le coeur est en polyméthacrylate de méthyle parcourue par un
faisceau laser ;
l’extrémité de la fibre plonge dans le goulot de la bouteille. Le
détecteur est sensible au flux
énergétique renvoyé par l’extrémité de la fibre. Le remplissage est
stoppé lorsque le niveau de
liquide atteint la pointe de la fibre.
3.1. Préciser, en
justifiant, la couleur de la lumière émise par la source laser.
Fréquence
4,75 1014 Hz ; longueur d'onde l = c / f = 3 108
/(4,75 1014) ~6,31 10-7 m =631 nm.
Couleur rouge.
3.2.
Expliquer le principe de la propagation guidée de la lumière au sein
d’une fibre optique.
Une explication détaillée (sans calcul) du phénomène physique mis en
jeu est attendue.
Illustrer les quelques lignes d’explication par un schéma soigné et
légendé du trajet d’un
rayon lumineux dans la fibre optique.
Un rayon R, injecté en O
dans le coeur de la fibre, demeure
prisonnier du coeur si son angle d'incidence i est bien choisi. on note
r l'angle sortant du coeur de la gaine ( i,r) et on note r' l'angle
incident à l'interface coeur gaine ( r + r'= 90 degrés)
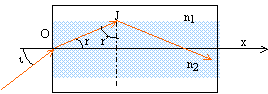
L'indice du coeur n2
doit être supérieur à l'indice n1 de la gaine.
L'angle limite d'incidence r' doit être tel que sin r' = n1
/ n2. Il y a réflexion totale en J.
Le rayon lumineux ne peut pas sortir de la fibre en J. La lumière est
guidée de l'entrée à la sortie de la fibre.
|
|
|
|
3.3. On s’intéresse au rayon
arrivant à l’extrémité épointée de la fibre, lorsque celle-ci plonge
dans la bière. Calculer ilim l’angle d’incidence limite à
l’interface fibre / bière. Indice de réfraction de la bière n = 1,34.
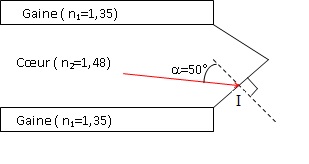
sin ilimite =n / n2 = 1,34 / 1,48 = 0,905 ;
ilimite ~64,9°.
Dans le cas où l’extrémité épointée de la fibre est dans l’air, l’angle
d’incidence limite à l’interface fibre / air est de 42,5 °.
3.4. Expliquer
pourquoi l’onde lumineuse est totalement réfléchie à l’interface fibre
/ air lorsque la fibre se trouve dans l’air, alors qu’elle n’est que
partiellement réfléchie lorsqu’elle plonge dans la bière.
A l'interface fibre /air, l'angle d'incidence (50°) est supérieur à
l'angle d'incidence limite. Il y a réflexion totale.
A l'interface fibre /bière, l'angle d'incidence (50°) est inférieur à
l'angle d'incidence limite. Il y a réfraction. la lumière est
partiellement réfléchie.
3.5. Expliquer le
principe de détection du niveau de liquide par ce dispositif ;
l’explication s’appuiera sur la comparaison qualitative des valeurs des
flux énergétiques reçus par le détecteur, suivant le milieu dans lequel
plonge l’extrémité de la fibre.
Le niveau n'est pas atteint : il y a réflexion totale dans la fibre. Le
capteur reçoit beaucoup de lumière en retour.
Le niveau vient d'être atteint. Il y a réflexion partielle. Le capteur
reçoit moins de lumière en retour.
Le niveau de remplissage est atteint lorsque le capteur perçoit une
baisse du flux lumineux.
|
|



