Tomographie par
émission de positons.
bac S Nlle Calédonie 03 / 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Le 18F-FDG(
noté FDG par la suite) est un dérivé du D-glucose contenant du fluor
18, isotope radioactif du fluor. Injecté à un patient juste avant un
examen appelé PET-scan, le 18F-FDG permet de localiser en direct les
zones de l'organisme qui consomment le plus de D-glucose, comme les
cellules du cerveau en activité. Cet exercice se propose d'étudier la
synthèse du FDG à partir de l'isotope 18 du fluor et son utilisation
comme marqueur radioactif lors de l'examen PET-scan.
1. Synthèse du FDG.
Le FDG est un dérivé du D-glucose dans lequel l'un des groupes
hydroxyle ( -OH) est remplacé par un atome de fluor 18
radioactif. La similitude de structure du FDG et du D-glucose
fait que le FDG est absorbé par les cellules biologiques de la même
façon que le D-glucose. Cependant la présence du fluor empêche ces
cellules de le dégrader pour produire de l'énergie. Le FDG demeure donc
plus longtemps dans les cellules.
Le FDG est produit au sein même des hopitaux qui en ont besoin par
réaction d'ion fluorure 18 avec un composé A représennté ci-dessous. La
réaction se déroule en deux étapes.
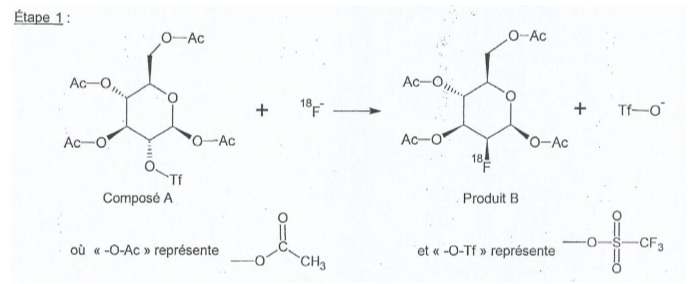
Lors d'une deuxième étape ( non décrite ici, on obtient le FDG à partir
du produit B.
1.1.
l'étape 1 est-elle une addition, une élimination ou une substitution ?
Justifier.
Lors de l'étape 1, le groupe O-Tf est remplacé par le 18F.
Le restant de la molécule est inchangé : il s'agit d'une substitution.
1.2. A l'aide du
formalisme des flèches courbes, matérialiser la formation et la rupture
de liaisons de l'étape 1.
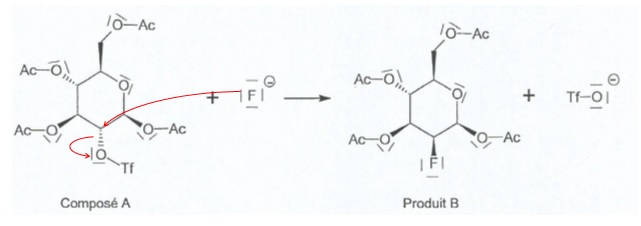
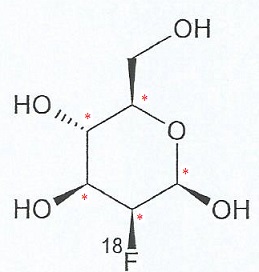
1.3. Indiquer par
un astérisque le(s) atome(s) de carbone asymétrique(s) de la molécule
de FDG.
|
|
|
2. Utilisation du FDG pour un diagnostic
médical.
Le FDG est injecté au patient sous forme d'une solution aqueuse par
voie intraveineuse.
Préparation de
l'injection.
A l'issue de la synthèse, on obtient une solution aqueuse de FDG de
concentration molaire 5,0 10-8
mol/L qu'il faut diluer pour pouvoir l'injecter au patient. Pour cela
on prélève 2,5 mL de solution aqueuse de FDG que l'on introduit dans un
flacon. On complète avec une solution saline pour obtenir 15 mL de
solution diluée.
2.1. Déterminer la
concentration de la solution contenue dans le flacon.
Facteur de dilution F = 15 / 2,5 = 6.
Concentration de la solution diluée : 5,0 10-8 / 6 = 8,3 10-9
mol/L.
Pour des raisons de sécurité, l'activité d'un flacon de 15 mL ne doit
pas dépasser Amax = 1,0 1010 Bq. L'activité A
d'un flacon de FDG est proportionnelle au nombre N de molécules de FDG
qu'il contient. On a A = lN
où A est exprimée en Bq et l
= 1,05 10-4 s-1.
2.2. Vérifier que
le flacon préparé respecte les consignes de sécurité.
N = 8,3 10-9 x0,015 x 6,02 1023 = 7,525 1013.
A = 1,05 10-4 x 7,525 1013 =7,9 109
Bq, inférieur à Amax.
On souhaite utiliser ce flacon de 15 mL ayant une activité de 7,9 109
Bq pour réaliser un examen sur plusieurs patients. le protocole médical
impose qu'on injecte à chaque patient une quantité de FDG dépendant de
la masse corporelle ( en kg). la dose recommandée est de 3,7 MBq kg-1.
2.3. ERstimer le
nombre de patients adultes à qui l'on pourrait injecter la dose
recommandée avec un flacon.
Masse moyenne d'un patient : m = 70 kg.
Dose recommandée pour un patient : 3,7 106 x70 ~2,6 108
Bq.
Nombre de patients : 7,9 109 / (2,6 108) ~30.
|
|
|
|
3. Production des ions 18F-
avec un cyclotron.
On bombarde au moyen d'un cyclotron, des noyaux d'oxygène 18 par des
protons dont l'énergie cinétique est de 16 MeV.
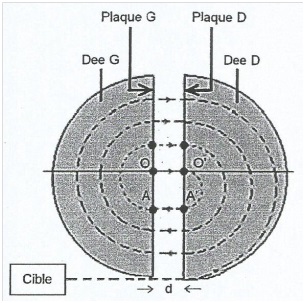
Le cyclotron est un appareil constitué de deux demi-cylindres creux
appelés dees. Entre les plaques G et D des dees règne un champ
électrique E uniforme perpendiculaire à ces plaques. On fait
l'hypothèse que le proton n'est pas relativiste et on admettra que son
poids est négligeable devant la force électrique. Les protons placés au
point O sont accélérés jusqu'au point O' où ils pénètrent dans le dee D.
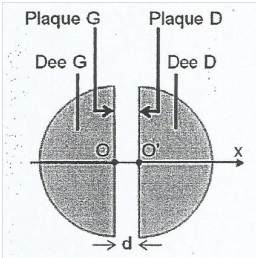
A
t=0, un proton est introduit dans le cyclotron au point O sans vitesse
initiale. La tension accélératrice vaut U = 30 kV. On se place sur
l'axe Ox horizontal, centré sur O, dirigé vers la droite.
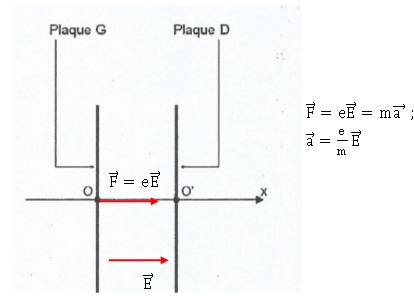
3.1. Sachant que le
proton doit être accéléré, compléter le schéma, sans souci d'échelle,
en y faisant figurer le vecteur F modélisant la force électrique
exercée sur le proton en O ainsi que le champ électrique E. Justifier.
3.2. Etablir
l'expression du vecteur accélération du proton en fonction du champ
électrique.
Le travail de la force électrique doit être moteur afin d'accélérer les
protopns. La charge électrique d'un proton est positive q = e.
Travail de la force F : W = e U positif ; par conséquence U = UGD
est positive.
La force F est dirigée de O vers O'. La charge étant positive, la force
et le champ électrique sont deux vecteurs colinéaires et de même sens.
3.3.
Montrer que l'abscisse x du proton sur le trajet OO' est donné par la
relation : x(t) = e|U| / (2md) t2.
La vitesse est une primitive de l'accélération : a
= e|U| / (md) ; v = e|U| / (md) t +
Constante.
A l'instant initial, la vitesse est nulle : 0 = Constante.
L'abscisse est une primitive de la vitesse : x(t) = e|U|
/ (2md) t2+ Constante.
A l'instant initial, la proton est en O, origine de l'axe : la
constante d'intégration est nulle.
Dans
le dee D, le proton soumis à un champ magnétique uniforme d'intensité B
= 1,6 T, a un mouvement circulaire uniforme jusqu'au point A'. Lorsque
le proton arrive au point A', le sens du champ électrique E est
inversé. Le proton subit alors une nouvelle accélération jusqu'au point
A.
Le processus d'accélération et de demi-tours successifs se répète un
grand nombre de fois jusqu'à ce que le proton sorte de l'accélérateur
avec la vitesse souhaitée pour bombarder la cible. Une dizaine de
microsecondes est nécessaire pour atteindre une telle vitesse.
3.5.
le mouvement du proton entre O' et A' est circulaire uniforme. En
déduire la relation entre la vitesse v du proton, le rayon R de la
trajectoire et la durée Dt2
de ce premier demi-tour.
Le proton décrit la demi circonférence pR à la vitesse v en Dt2
seconde
; v = pR / Dt2.
Le rayon R de la
trajectoire d'un proton dans un dee est donné par la relation R = mv
/(eB) où v est la vitesse du proton.
3.6.
Montrer que Dt2
peut s'exprimer sous la forme Dt2 =
pm /
(eB). En déduire que tous les demi-tours ont la même durée.
Dt2
=
pR / v avec R / v = m / (eB)
; Dt2
= pm / (eB).
Dt2
est indépendante du rayon R et B est
constant : tous les demi-tours ont la même durée.
3.7. En considérant
que la durée Dt1
d'une phase d'accélération est de l'ordre de 2 ns, montrer que Dt2 est
environ 10 fois plus grande.
Par la suite on considèrera que
Dt1
est négligeable devant
Dt2.
Dt2
=3,14 x1,67 10-27 /(1,6 10-19
x1,6) ~2,0 10-8 s ~20 ns.
3.8. Evaluer le
nombre de tours que doit faire le proton pour qu'il atteigne, à la
sortie du cyclotron, une énergie de 16 MeV. Evaluer la durée pour que
le proton sorte du cyclotron et comparer la valeur obtenue avec celle
du texte.
A chaque passage entre les dees, l'énergie du proton augmente de eU
joule ou U électron-volts, soit 30 keV ; à chaque tour, l'énergie du
proton croît de 60 keV.
Nombre de tours : 16 103 / 60 ~267 tours.
Durée correspondante : .267 x 40 10-9~1,0 10-5 s
ou environ 10 µs.
Cette valeur est en accord avec le texte : " Une
dizaine de microsecondes est nécessaire pour atteindre une telle
vitesse.".
|
|
|
|