Interférence avec des atomes froids. bac S Liban 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . A toute particule matérielle de masse m et de vitesse v est associée une onde de matière de longueur d'onde l  : l = h / p. h est la constante de Planck et p la quantité de mouvement de la particule. Un gravimètre à atomes froids utilise un dispositif vertical dont le principe de fonctionnement est schématisé ci-dessous Il utilise des atomes de néon piégés et refroidis à une température de 2,5 millikelvins. Ces atomes quittent le piège sans vitesse initiale et tombent dans le champ de pesanteur g. 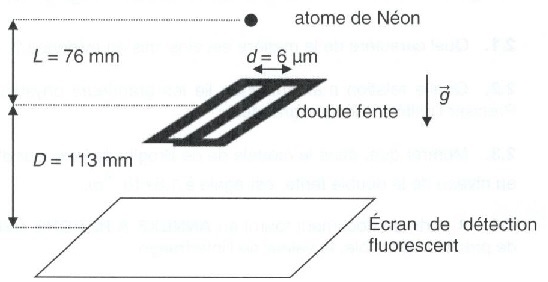Le piège est situé à une hauteur L au dessus de deux fentes.Un écran de détection est placé à une distance D des deux fentes : il permet de détecter chaque impact d'atome de néon. On obtient sur l'écran une figure d'interférences constituée d'environ 6000 impacts d'atomes. Masse d'un atome de néon : m = 3,35 10-26 kg ; h = 6,63 10-34 J s ; vitesse des atomes au niveau de la double fente ; v = 1,2 m /s.  1. Chute de l'atome avec le modèle de Newton. 1. 1. Montrer que la vitesse d'un atome au niveau de la double fente est verticale et que sa valeur est donnée par v = (2gL)½. L'atome n'est soumis qu'à son poids, vertical vers le bas, valeur mg. Sa chute est libre suivant la verticale descendante. Le vecteur vitesse est tangent à la trajectoire verticale. Variation de l'énergie cinétique de l'atome entre l'instant de départ et la double fente : ½mv2 -0. Travail moteur du poids : mg L. Le théorème de l'énergie cinétique conduit à  : ½mv2 = mgL ; v =(2gL)½. 1.2. Dans le cadre de la mécanique de newton, on suppose que les atomes issus du piège arrivent sur les fentes avec une vitesse égale à ( 2gL)½. Dans cette hypothèse, dessiner la répartition d'un grand nombre d'atomes détectés sur l'écran. Un impact est représenté par un point noir. Vue de dessus 2. Le modèle de de Broglie. La figure obtenue sur l'écran est une figure d'interférences. 2.1 Quel caractère de la matière est mis en évidence ? Les interférences mettent en évidence le caractère ondulatoire de la matière. 2.2 Quelle relation mathématique lie les grandeurs p, m et vF au niveau de la fente ? Préciser l'unité de chaque grandeur. p = m vF. p quantité de mouvement en kg m s-1 ; m  : masse en kg et VF vitesse en m s-1. 2.3. Montrer que dans ce modèle la longueur d'onde associée à l'atome de néon au niveau de la double fente est égale à 1,6 10-8 m. lth = h /(m vF)=6,63 10-34 / (3,35 10-26 x1,2) = 1,6 10-8 m. 2.4. Déterminer la largeur de l'interfrange. 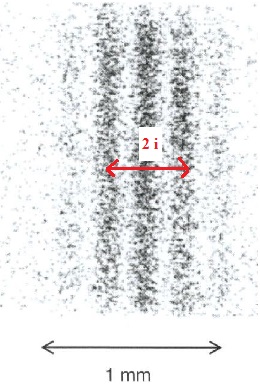i ~0,24 mm. .............. ................. 2.5. Déterminer parmi les propositions suivantes, la formule qui permet de calculer l'interfrange à partir des caractéristiques de l'expérience. Préciser la méthode utilisée. i = lD / d ; l, D et d sont des longueur ; la relation est homogène.  i = l2d/D ; i = dD / l2. Ces deux relations ne sont pas homogènes. 2.6 et 7. Comparer lth et lexp. lexp.=id / D = 0,24 10-3 x6 10-6 / 0,113=1,27 10-8 ~1 10-8 m. lth et lexp sont du même ordre de grandeur. 2.8.1 Après les deux fentes la mécanique classique ne peut plus être utilisée. par contre la gravitation continue de s'exercer après les fentes. Comment évolue la quantité de mouvement associée aux atomes de néon entre la double fente et l'écran ? Les atomes sont en chute libre. Leur vitesse croît et leur quantité de mouvement augmente. 2.8.2. Comparer qualitativement la longueur d'onde associée aux atomes de néon au niveau de la double fente et au niveau de l'écran. l = h / p, si p augmente alors la longueur d'onde diminue. 2.8.3. A quelle longueur d'onde aurait-on dû comparer la longueur d'onde obtenue expérimentalement. A la longueur d'onde au niveau de l'écran. .

menu