La mécanique au service de la pétanque. bac S Liban 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Cet exercice aborde le lancer d'une boule par le pointeur, puis par le tireur. Les frottements sont négligés. Partie A. Le pointeur. Le pointeur lance une boule de masse m = 710 g avec une vitesse initiale v0 faisant un angle a avec l'horizontale. l'origine O est prise au point où le pointeur lâche la boule. Le modèle de la chute libre conduit aux équations horaires suivantes du centre G de la boule dans le repère ( O, x, y). x=v0 cos a t ; y = -0,5gt2 +v0 sin a t. Intensité du champ de pesanteur sur terre g = 9,81 m s-2. 1. On réalise une chronophotographie du mouvement de la boule lancée par le pointeur. L'intervalle de temps entre deux prises de vues est de 33,3 ms. Quelques coordonnées du centre de la boule. Date t(s) x(m) y(m) 0 0 0 0,033 0,117 0,117 0,067 0,243 0,243 0,100 0,346 0,360 1. 1. Déterminer la valeur de l'angle a en précisant la méthode choisie. 1.2. Déterminer la valeur de la vitesse initiale V0.. 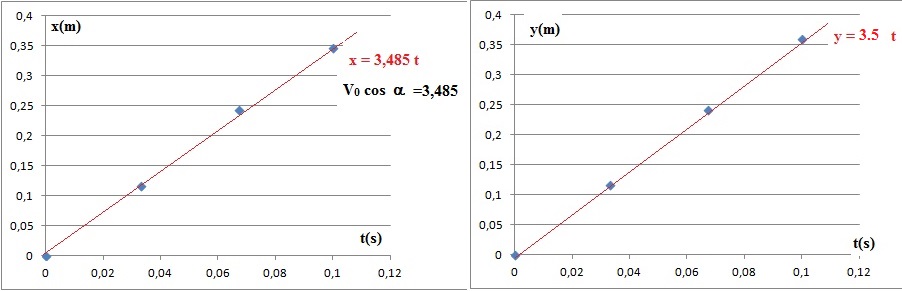Pour t < 0,07 s, on remarque y est peut différent de v0 sin a t. Par suite y / x = tan a = 3,5 / 3,485 = 1,004 ; a ~45°. Par suite v0 = 3,485 / cos45 ~5,0 m /s. 2. Le pointeur lance la boule en direction du bouchon et la lâche au point O, origine du repère choisi. O est situé a une hauteur de 1,2 m du sol. . 2.1. Montrer que la boule suit la trajectoire parabolique d'équation y = -½gx2 / (v0cosa)2 +tan a x. t = x / (v0 cos a ), repport dans y : y = -½gx2 / (v0cosa)2 +v0 sin a / (v0 cos a)x. y = -½gx2 / (v0cosa)2 +tan a x. 2.2. Pour un angle a = 51° et une vitesse initiale égale à 5,5 m/s, la boule touche le sol puis roule vers le bouchon. Calculer l'abscisse du point d'impact avec le sol. Au sol y = -1,2 m ; -1,2 = -0,5 *9,81 x2 /(5,5 *cos51)2 + tan 51 x. -1,2 = -0,4094 x2 +1,2349 x. 0,4094 x2 -1,2349 x -1,2 =0. Discriminant :1,23492 +4x1,2 x0,4094 =3,49. Racine carrée du discriminant : 1,868. Abscisse du point d'impact au sol : (1,2349 +1,868) / (2x0,4094) ~3,8 m .............. ................. Partie B. le tireur. La boule lancée par le pointeur étant proche du bouchon, le tireur adverse va chercher à la déplacer. Le tireur lance sa boule à quelques centimètres de la boule visée ; la boule du tireur roule puis percute la boule du pointeur de plein fouet avec une vitesse v2 = 8,0 m /s. Dans le référentiel terrestre , après le choc, les deux boules de masses respectives m1 et m2, possèdent les vecteurs vitesses V'1 et V'2 portées par la même direction. 1. Nommer les grandeurs qui se conservent lors du choc. 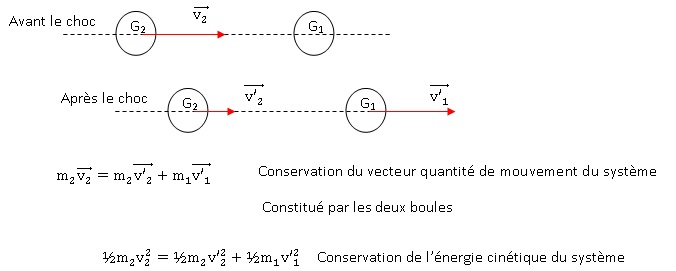2. La résolution du système précédent permet d'écrire les relations vectorielles suivantes : A partir de ces relations, associer les relations A, B et C comparant les masses aux trois propositions 1, 2et 3. Justifier. m1 = m2. v'2 est nulle ; v'1 = v2 : les boules échangent leurs vitesses. m1 > m2 : v'2 est négative, la boule G2 repart en sens inverse. m1 < m2 : v'2 est positive, la boule G2 suit la boule G1. 3. Que se passe t-il si m1 est très largement supérieure à m2 ? v'1 est proche de zéro ; v'2 est négative et proche de v2. La boule G2 rebondit sur la boule G1 qui ne bouge pratiquement pas. .

menu