Observation d'une exoplanète, bac S Antilles 09 /2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . L’existence de planètes situées en dehors du système solaire (ou exoplanètes) fait l’objet d’études scientifiques depuis le XIXème siècle. Leur éloignement, mais aussi leur manque de luminosité par rapport aux étoiles autour desquelles elles tournent, rendent leur détection difficile. 1. Comment la diffraction rend-elle difficile l’observation d’une exoplanète ? Un télescope de diamètre D collecte la lumière émise par un objet céleste, puis la renvoie vers un système optique de formation d’image qui ne sera pas étudié ici. Actuellement, l’observation de détails avec un télescope terrestre est principalement limitée par le phénomène de diffraction lié à la valeur de l’ouverture circulaire D du télescope car il est possible d’annuler l’effet des turbulences atmosphériques sur la qualité des images formées. La première planète extrasolaire dont on a pu faire une image par observation directe dans le proche infrarouge s’appelle M1 07b. Cette exoplanète orbite à une distance estimée à 55 unités astronomiques (ua) autour de l’étoile 2M1207a, située à 230 années lumières (al) de la Terre. Document 1 : Diffraction par une ouverture circulaire. 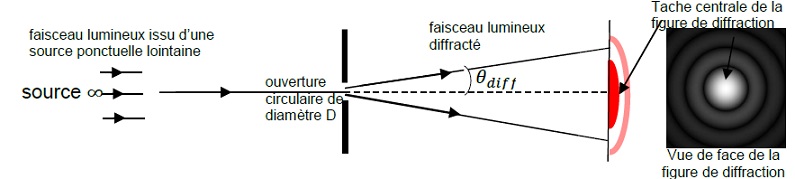Dans le cas d’une ouverture circulaire, on admet que l’angle de diffraction q diff (exprimé en radian) vérifie la relation q diff =1,22 l / D , où l est la longueur d’onde du faisceau incident et D le diamètre de l’ouverture. Écart angulaire et diffraction. Des rayons lumineux issus d’un couple étoile-planète et passant par l’ouverture circulaire d’un télescope terrestre sont représentés dans le schéma ci-dessous : 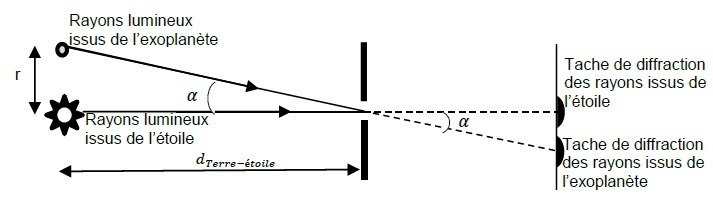a est l’écart angulaire entre l’étoile et la planète, c’est à dire l’angle sous lequel l’écart angulaire étoile-planète est vue depuis la Terre. Il se calcule grâce à la relation : a ~tan a= r / dterre-étoile. où r est la distance entre la planète et l’étoile et d terre-étoile la distance entre la Terre et l’étoile. Critère de Rayleigh pour distinguer deux objets. Un télescope permet de distinguer deux objets à condition que l’écart angulaire entre ces deux objets soit supérieur ou égal à l’angle de diffraction qdiff. .... ..... Données : unité astronomique : 1 ua =1,496 1011 m ; l’année lumière : 1 al =9,461 1015 m ; vitesse de la lumière dans le vide : 3 108 m s-1. 1.1. Quelle propriété de la lumière permet d’expliquer le phénomène de diffraction ? La diffraction met en évidence le caractère ondulatoire de la lumière. 1.2. Déterminer le diamètre minimal D du télescope terrestre permettant de distinguer la planète 2M1207b de l’étoile M1 07a. On admet que la longueur d’onde des rayons lumineux provenant des deux objets célestes a pour valeur 2,0 µm. a ~tan a= r / dterre-étoile = 55 x1,496 1011 / (230 x9,461 1015) =3,7812 10-6 rad. q diff =1,22 l / D. 1,22 l / D >3,7812 10-6  ; D >1,22 l / (3,7812 10-6). D > 1,22 x2,0 10-6 / (3,7812 10-6) ; D >0,65 m. 2. Comment la faible luminosité d’une exoplanète la rend-elle difficile à observer ? En général, les planètes sont peu lumineuses par rapport aux étoiles ce qui ajoute une difficulté supplémentaire pour les observer. Un dispositif interférométrique, décrit dans le document 2, a été proposé en 1978 par le physicien australien Ronald N. Bracewell. Il permet de contourner ce problème. L’objectif est d’éliminer le signal de l’étoile tout en permettant l’enregistrement du signal émis par la planète. Document 2 : Dispositif interférométrique On considère deux télescopes identiques dont les lignes de visées sont dirigées vers une étoile lointaine. La direction d’une exoplanète à proximité de l’étoile fait un angle a avec la ligne de visée.   Dans ce dispositif, les faisceaux issus des deux télescopes sont recombinés grâce à un dispositif optique situé à égale distance des deux télescopes. Recombinaison des signaux issus de l’étoile 2.1. Justifier que, dans le dispositif décrit dans le document 2, les rayons lumineux issus de l’étoile et captés par les télescopes 1 et 2 interfèrent de façon constructive au niveau de la recombinaison. La différence de marche entre les deux faisceaux lumineux est nulle, égale à un nombre entier de longueur d'onde. 2.2. On appelle T la période de l’onde lumineuse. L’idée de Bracewell est d’ajouter, juste après le télescope 2, un système optique permettant d’ajouter un retard d’une demi-période sur le signal provenant de ce télescope. Montrer que ce système optique produit des interférences destructives entre les deux rayons issus de l’étoile au niveau de la recombinaison. Quelle sera alors l’intensité du signal lié à l’étoile ? La différence de marche entre les deux faisceaux lumineux est égale à c T / 2 = ½l. La différence de marche étant égale à un multiple impair de la demi longueur d'onde, les interférences seront destructrices. L'intensité du signal de l'étoile sera minimale voir nulle. Recombinaison des signaux issus de l’exoplanète Les rayons lumineux issus de l’exoplanète arrivent sur les dispositifs interférométriques en faisant un angle a avec la ligne de visée. À cause de cette inclinaison, le signal lumineux arrive sur le télescope 2 avec un retard t=d.sin a / c, où d est la distance entre les deux miroirs m. 2.3. Montrer que le signal issu du télescope 2 a un retard de t'=d.sin a / c +½T par rapport au signal issu du premier télescope. Un système optique permet d’ajouter un retard d’une demi-période sur le signal provenant du télescope 2. L'inclinaison introduit un retard supplémentaire t=d.sin a / c. 2.4. À quelle condition sur le retard t’ va-t-on obtenir une interférence constructive ? La différence de marche entre les signaux qui interfèrent est égale à ct' = d.sin a +0,5 cT = d.sin a +0,5 l. Les interférence seront constructives si : d.sin a +0,5 l = k l avec k entier. 2.5. Montrer que cette relation peut aussi s’écrire d.sin a=(k-0,5)l , k étant un nombre entier. d.sin a +0,5 l = k l soit  d.sin a=(k-0,5)l . 2.6. Pour des petits angles, sin a ~tan a  =r / dterre-étoile, en déduire la distance minimale d entre les deux télescopes pour obtenir une interférence constructive lors de l’observation de l’exoplanète M1 07b en rotation autour de l’étoile M1 07a sachant que l’on travaille en infrarouge l= 10 µm. k=1 ; a=3,7812 10-6 rad ; d.sin a=(k-0,5)l . d ~0,5 l / a ; d ~0,5 10-5 / (3,7812 10-6)~1,3 m. .

menu