Le radon,
ultrasons, électrostatique.
Concours EMIA 2012.
école militaire interarmes
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1
: le radon 2 / 20.
Le radon 222 ( 22286Rn)
est le plus courant des gaz rares. C'est un gaz radioactif d'origine
naturelle, provenant de la désintégration de l'uranium 238 23892U. Sa concentration dans l'atmosphère est très faible, car il se désintègre rapidement en 21884Po par radioactivité alpha. Sa demi-vie est t ½ = 3,823 jours.
1.1. Pour passer de 23892U à 22286Rn on doit envisager plusieurs transformations successives de type alpha et béta -. Donner l'équation bilan d'une désintégration alpha d'un noyau AZX.
AZX ---> A-4Z-2X + 42He.
Donner l'équation bilan d'une désintégration ß- d'un noyau AZX.
AZX ---> AZ+1X + 0-1e.
En déduire le nombre de désintégrations alpha et ß - pour passer de 23892U à 22286Rn.
Nombre de désintégration alpha : (238-222) / 4 = 4.
Nombre de désintégration ß- :86+8-92=2.
On étudie l'activité d'un échantillon contenant du radon 222. On compte
à l'aide d'un appareil adapté le nombre de désintégrations pendant 20
s. On effectue 6 relevés espacés de 5 s et on obtient les valeurs
suivantes 506, 490, 494, 510, 502 et 498.
1.2. Pourquoi le résultat des mesures n'est-il pas constant ?
Propriétés d'une
désintégration :
Aléatoire : Il est impossible de
prévoir l'instant où va se produire la
désintégration d'un noyau radioactif.
Spontanée : La
désintégration se produit sans aucune
intervention extérieure.
Inéluctable : Un noyau radioactif se
désintégrera tôt ou tard.
Indépendante de la combinaison chimique dont
le noyau radioactif fait partie.
Indépendante des paramètres
extérieurs tels que la pression ou la
température.
1.3. L'activité de l'échantillon est-elle en cause ?
Non, la durée des mesures est très inférieure à la demi-vie radioactive du radon 222.
1.4. Calculer l'activité moyenne du radon au moment de l'expérience.
(506 +490 +494 +510 +502 +498) / 6 =500 désintégrations en 20 s.
A = 500 / 20 = 25 Bq.
1.5. Qu'appelle-t-on
période ou demi-vie d'un radioélément ?
La demi-vie radioactive,(ou
période) notée t½, d'un échantillon de noyaux radioactifs est égale à
la durée au bout de laquelle la moitié des noyaux radioactifs initiaux
se sont désintègrés.
1.6. Quelle est la relation entre la demi-vie radioactive et la constante radioactive l ?
t ½l = ln2.
1.7. Calculer la valeur de la constante radioactive du radon. l = ln2 / (3,823*24*3600)=2,098 10 -6 s -1.
1.8. Combien de noyaux de radon 222 étaient présents dans l'échantillon au moment de l'expérience ?
N = A / l = 25 / (2,098 10 -6)=1,19 10 7 .
|
|
|
Ondes ultrasonores : 3 / 20.
2.1.
Donner trois propriétés importantes d'une onde mécanique progressive.
Une onde mécanique progressive nécessite un milieu de propagation. Elle ne transporte pas de matière mais de l'énergie.
2.2. Définir ce qu'est une onde mécanique transversale et donner un exemple.
La direction de déformation du milieu est perpendiculaire à la direction de propagation. Exemple : la houle.
2.3. Définir ce qu'est une onde mécanique longitudinale et donner un exemple.
La direction de déformation du milieu est identique à la direction de propagation. Exemple : les onde sonores.
2.4. Les
ondes ultrasonores sont-elles perçues par l'homme ? Sinon, quel est le
domaine de fréquences des ondes sonores audibles par l'homme ?
Domaine de fréquences des ondes sonores perçues par l'homme : 20 Hz à 20 kHz.
L'homme ne perçoit pas les ultrasons ( fréquences supérieures à 20 kHz).
2.5.
Quelle grandeur caractérisant la propagation des ondes est sensible à un changement d'élasticité du milieu ?
La célérité de l'onde et en conséquence la longueur d'onde.
2.6.
Les ondes ultrasonores sont émises par un transducteur électrocapacitif
permettant de convertir un signal électrique périodique en l'émission
d'une onde ultrasonore de même période T. On dispose d'un transducteur
émettant des salves d'ultrasons, de deux détecteurs identiques et d'un
oscilloscope à deux voies. Le signal reçu sur la voie 1 est représenté
ci-dessous :
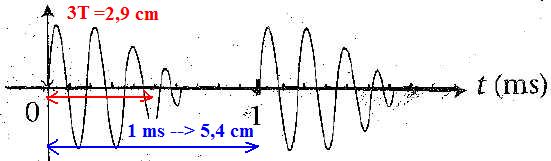
a. Commenter
l'évolution temporelle du signal en donnant les valeurs numériques de
deux caractéristiques importantes de l'onde ultrasonore reçue que l'on
peut déduire de cet enregistrement.
L'intervalle de temps séparant l'émission de chaque salve est égale à 1 ms.
La période des ultrasons est voisine de 0,18 ms ; soit une fréquence de 1 / 0,18 ~5,6 kHz.
( Remarque : la fréquence des ultrasons est supérieure à 20 kHz ).
b. Représenter l'allure du signal observé sur la voie 2 de l'oscilloscope en prenant la même origine des temps.
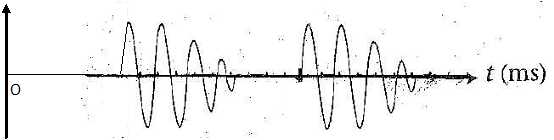
Une
série de mesure est réalisée en faisant varier la distance d entre les
deux détecteurs et en relevant à chaque fois le retard t entre l'arrivée des signaux sur les deux voies.
| d( cm) | 20 | 45 | 86 | 104 | 126 | 150 | | t(ms) | 0,59 | 1,30 | 2,50 | 3,10 | 3,70 | 4,42 |
2.7. Tracer la courbe de votre choix permettant de déterminer la célérité des ultrasons.
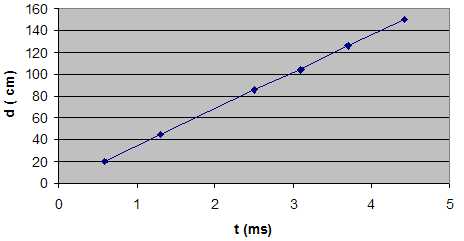
Pente =distance / temps = célérité : 33,8 cm ms-1 ou 338 m s-1.
Au cours d'une seconde expérience, on alimente le transducteur émetteur par une tension sinusoïdale de fréquence f = 40 kHz
2.8. Lorsque le retard t est égal à une période T de l'onde, quelle distance sépare les deux détecteurs ?
d = c T = c / f = 338 / (40 103) ~8,5 10-3 m.
2.9. Quelle est la relation entre la longueur d'onde l et la période T de l'onde ?
l = c T avec c : célérité de l'onde en m/s.
2.10. En prenant la valeur de la célérité déterminée précédemment, calculer l.
l = c / f = 338 / (40 103)~8,5 10-3 m.
|
|
|
|
3. Electrostatique.
On considère une sphère de rayon R chargée uniformément en volume avec une densité volumique r et qui porte également une charge surfacique uniforme de densité s sur sa surface. On donne r = q / (4/3 p R3) et s = -q /(4pR2).
3.1. Montrer que la charge totale du système est nulle.
Charge portée par la surface : -q ; charge interne à la sphère : +q ; charge totale -q+q=0.
3.2.
Enoncer le théorème de Gauss.
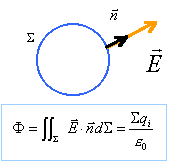
D'après le théorème de Gauss, le flux du vecteur champ
électrique à travers la surface S
est égal à la somme des charges situées à l'intérieur de S divisée par e0. 3.3. A l'aide du théorème de Gauss, montrer que le champ électrostatique est nul en tout point extérieur à la sphère chargée.
Appliquer le théorème de Gauss : la surface de Gauss
est une sphère de rayon r > R.
4pr2 E =0 ; E = 0.
3.4. Déterminer l'expression du
champ électrostatique en un point M situé à l'intérieur de la sphère chargée. On pose OM = r.
La surface de Gauss
est une sphère de rayon r < R.
4pr2 E =4/3 pr3 r / e0 ; E = r r / (3e0 ).
3.5. Déterminer le potentiel V(M) en tout point de l'espace. On prendra le potentiel nulà l'infini.
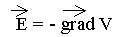
A l'extérieur de la sphère V= constante = 0.
A l'intérieur de la sphère : V(M) = - r2 r / (6e0 ) + constante.
3.6. Une
particule ponctuelle de masse m et de charge q rencontre la sphère
selon une trajectoire rectiligne qui passe par O. Elle est émise avec
la vitesse v au niveau d'une cathode C située à la distance 2R de O.
Pour quelles valeurs de la vitesse v la particule peut-elle
traverser la sphère ?
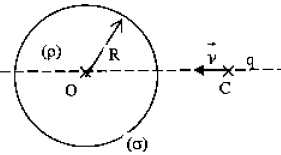
Tant
que la particule est à l'extérieur de la sphère, elle n'est soumise à
aucune force électrique, la charge globale de la sphère étant nulle.
A l'intérieur de la sphère, la particule de charge q est soumise à une force électrique F = q E = q r r / (3e0 ), répulsive. Cette force est maximale lorsque r est voisin de R.
Le poids de la particule est négligeable devant la force électrique. Le travail du poids, perpendiculaire à la vitesse, est nul.
Travail résistant de cette force électrique : 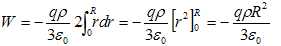
Variation de l'énergie cinétique lors de la traversée de la sphère ( dans le cas d'une vitesse nulle à la sortie ) :
0-½mvmini2 = -qrR2 / (3e0).
vmini2 =2qrR2 / (3me0).
|
|