Schéma de Thévenin, circuit RLC, amplificateurs opérationnels. Concours EMIA 2011.
école militaire interarmes

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



Schéma de Thévenin ( 2 / 20).
On considère le circuit suivant comportant une source de tension, une source de courant, trois résistances et une diode idéale D.
E1 = 25 V ; I2 = 1 A ; R1 = 10 ohms ; R2 = 20 ohms ; R = 10 ohms.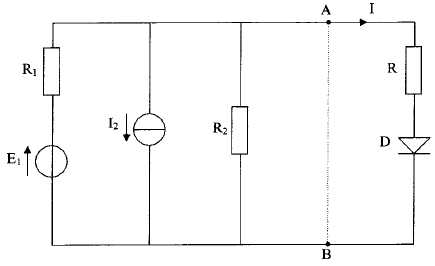

1. On cherche à établir le schéma équivalent de Thévenin de la partie gauche du circuit vue entre les points A et B.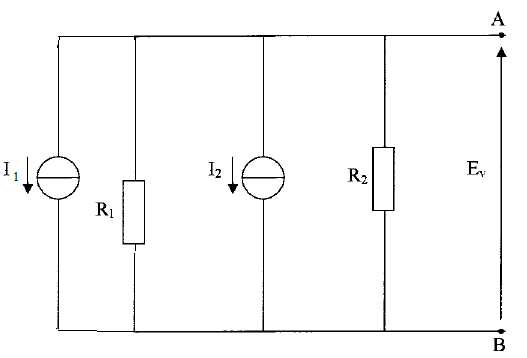

I1 = E1 / R1 = 25 / 10 = 2,5 A.
On retire les sources  et on calcule la résistance de Thévenin :
R1 et R2 sont en parallèles : Ri =R1R2 / (R1+R2) = 10*20 / 30 ~6,7 ohms.
On laisse les sources  et on met AB en court-circuit ;
Ev étant nulle, les résistances R1 et R2 sont traversées par aucun courant.
L'intensité Icc du courant est :
Icc = I1+I2 = E1 / R1 +I2= 1 +2,5 = 3,5 A.
 Fem du générateur équivalent de Thévenin Ev = Ri Icc=6,7 *3,5 ~23,3 V.
2. Courant traversant la diode D.
. 
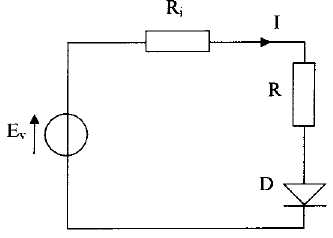La diode traversée par un courant I est équivalente à un interrupteur fermé. Déterminer I en fonction de Ev, R et Ri puis en fonction de E1, I2, R1, R2 et R. Faire l'application numérique.
I = Ev / (R+Ri) = 23,3 / (10+6,7) = 1,4 A.
 Ri =R1R2 / (R1+R2) ; Icc = E1 / R1 +I2 ; Ev = [R1R2 / (R1+R2)] [E1 / R1 +I2].
I = [R1R2 / (R1+R2)] [E1 / R1 +I2]. / [R+R1R2 / (R1+R2)].
.
.




Etude d'un circuit RLC ( 2 / 20).
La tension d'entrée est sinusoïdale e(t) = E sin ( wt).

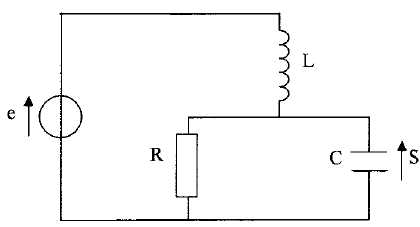
1 Fonction de transfert T(jw)..
1.1. Exprimer l'impédance Zc du condensateur.
Zc = 1 / (jCw).
1.2. Exprimer l'admittance Yéq puis l'impédance Zéq de l'association parallèle constituée par la résistance R et le condensateur C.
1.3. Exprimer l'impédance ZL de la bobine.
  1.4. En utilisant le diviseur de tension, exprimer la tension S en fonction de e, R,L, C et w.
1.5. Exprimer la fonction de transfert T(jw) = S / e.

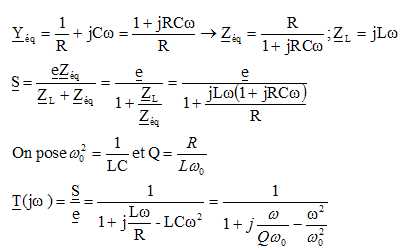
 1.7. On donne R = 10 ohms, L = 1 mH et C = 1 mF. Que valent Q et w0 ?
w0 = 1/(LC)½ = 1 103 rad/s ; Q = 10.
2. Caractérisation de la fonction de transfert.
2.1. Calculer la limite de T(jw) quand w tend vers zéro.
T(jw) tend vers 1.
2.2 . Calculer la limite de T(jw) quand w tend vers l'infini.
T(jw) tend vers 0.
2.3. Calculer T(jw0) en fnction de Q.
T(jw0) = -j Q.
2.4. Déduire des questions précédentes la nature du filtre en justifiant.
2.5. Exprimer le gain G(w) en fonction de w, w0 et Q.
2.6. Tracer l'allure du G(w). Annoter le graphe pour faire apparaître les éléments importants..
Le gain représente la norme de la fonction de transfert.

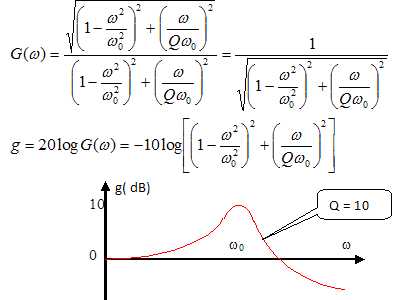
Le graphe ci-dessus indique qu'il s'agit d'un filtre basse bande ; g présente un maimum  pour w proche de w0.









Circuit à amplificateur opérationnel ( 2 / 20).
L'AO est idéal et fonctionne en régime linéaire. On impose à l'entrée une tension e(t) sinusoïdale de pulsation w.

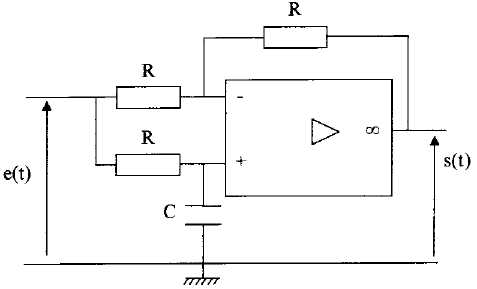
1. Fonction de transfert T(jw) = s(t) / e(t).
1. Etablir l'expression de la tension sur l'entrée non inverseuse.
2. Etablir l'expression de la tension sur l'entrée  inverseuse.
3. En déduire la fonction de transfert.
 4. Donner l'expression du gain.
5. Donner l'expression du déphasage f. Pour quelle pulsation vaut-il -½p ?

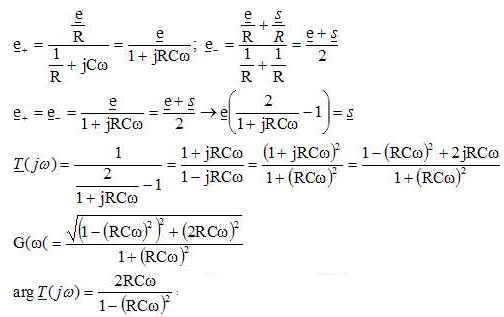
tan f = argT(jw).
Si f = -½p, tan f tend vers moins l'infini.
w tens vers 1 / (RC).
2. Quel est le rôle de ce circuit ?
C'est un circuit déphaseur.

.


  

menu