Radioactivité artificielle, ondes, électrostatique. Concours EMIA 2013. école militaire interarmes En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1 : radioactivité artificielle et fission nucléaire 3 / 20. 1. Le polonium.  1.1. Qu'est ce qu'un noyau radioactif ? Un noyau radioactif est un noyau instable dont la désintégration (destruction) aléatoire s'accompagne : L'apparition d'un nouveau noyau L'émission d'une particule notée a, ß - ou ß + L'émission d'un rayonnement électromagnétique noté g. 1.2. Qu'est ce qu'une particule alpha ? Une particule alpha est un noyau d'héliumnotée 42He. 1.3. Ecrire l'équation de la réaction nucléaire pour une émission alpha d'un noyau de polonium 210 21084Po. 21084Po --->20682Pb + 42He.   2. Irradiation de l'aluminium. En présence d'une source de polonium, un noyau d'aluminium, composé de 13 protons et 14 neutrons, capture une particule alpha et émet immédiatement un neutron. Le noyau fils obtenu est un isotope instable du phosphore composé de 30 nucléons dont 15 protons. Le phosphore radioactif se désintègre à son tour en silicium stable en émettant un positon.   2.1. Ecrire l'équation de la réaction nucléaire permettant de passer de l'aluminium stable au phosphore instable. 2713Al + 42He ---> 3015P+10n. 2.2. Définir isotopes. Des isotopes ne se différencient que par leur nombre de neutrons. Ils ont le même numéro atomique Z. 2.3. Ecrire l'équation de la réaction nucléaire de désintégration du phosphore instable en silicium. 3015P ---> 3014Si+01e. 2.4. De quel type de radioactivité s'agit-il ? Radioactivité de type ß+. 2.5. Tracer l'allure du graphe de l'évolution temporelle du nombre de noyaux de phosphore dans un échantillon contenant initialement N0 noyaux de phosphore instable. 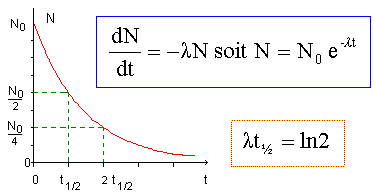2.6. Qu'appelle-t-on période ou demi-vie d'un radioélément ? La demi-vie radioactive,(ou période) notée t½, d'un échantillon de noyaux radioactifs est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés. 2.7. La demi-vie du phosphore 30 est de 2 min 55 s, calculer la constante radioactive de ce noyau. l = ln2 / t½ = ln2 / (2*60+55)=3,96 10-3 s-1. Exercice II : questions diverses 4 /20. 1. Les ondes : 1.1. Donner un exemple d'onde mécanique transversale. La houle. 1.2. Donner un exemple d'onde mécanique longitudinale. Une onde sonore. Grâce à un vibreur électromécanique fixé à l'extrémité d'une corde tendue mesurant 10 m de longueur, on étudie la propagation d'une onde sinusoïdale sur cette corde. Le vibreur est alimenté par un générateur basses fréquences GBF et on admet que les oscillations mécaniques se font à la même fréquence. Pour tester le dispositif on débranche le vibreur et on créé manuellement une perturbation à l'extrémité de la corde. On constate que cette perturbation se déplace le long de la corde tendue et qu'elle atteint l'autre extrémité au bout de 0,8 s. 1.3. Calculer la célérité de l'onde. v = 10 / 0,8 = 12,5 ~13 m /s.  1.4. On admet que cette célérité est la même pour toutes les fréquences utilisées lors des expériences. Comment qualifie-t-on le milieu de propagation ? La corde tendue est un milieu non dispersif pour ce type d'onde. 1.5. La fréquence du GBF est réglée à 40 Hz, calculer la longueur d'onde. l = v / f = 12,5 / 40 =0,3125 ~0,31 m. 1.6. Décrire une expérience simple permettant de mettre en évidence le caractère ondulatoire de la lumière. Diffraction par une fente ou par un fil dont les dimensions sont du même ordre de grandeur que la longueur d'onde de la lumière. Le classique laser hélium-néon émet une lumière rouge de longueur d'onde  dans le vide l0 = 633 nm. 1.7. Calculer la vitesse à laquelle cette radiation se propage  dans un verre d'indice n = 1,5. v = c / n = 3,0 108 /1,5 = 2,0 108 m/s. 1.8. La couleur associée à cette radiation varie-telle quand elle traverse le verre ? Non, la couleur est liée à la fréquence et celle-ci est constante quel que soit le milieu de propagation. 2. Electrostatique. Soient deux charges ponctuelles q1 et q2 situées aux points A et B distants de AB=r et placées dans le vide de permitivité e0. 2.1. Donner l'expression vectorielle de la foce électrostatique crée par la charge qA sur la charge qB et la représenter sur un schéma. 2.2. Enoncer le théorème de Gauss. D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est  égal à la somme des charges situées à l'intérieur de S divisée par e0. On considère un plan infini uniformément chargé en surface ( densité surfacique de charge s ). 2.3. Quelles sont les caractéristiques du vecteur champ électrique en tout point de l'espace ? La distribution de charge est invariante par translation suivant Ox : le champ ne dépend pas de la variable x. La distribution de charge est invariante par translation suivant Oy : le champ ne dépend pas de la variable y. La distribution de charge est invariante par translation suivant Oz : le champ ne dépend pas de la variable z. La distribution de charge est invariante par rotation de l'axe Oz : le champ ne dépend pas de l'angle q. Le champ électrostatique ne dépend pas des variables x, y et z. Tout plan contenant l'axe Oz est plan de symétrie pour la distribution de charge : le champ électrostatique est donc porté par l'axe Oz. 2.4. Déterminer l'expression du champ électrostatique en tout point de l'espace. Appliquer le théorème de Gauss : la surface de Gauss est un cylindre de section dS. Le flux du champ est nul à travers la surface latérale du cylindre, celle-ci étant perpendiculaire au champ. 2.5. Quelle relation lie le champ électrostatique et le potentiel électrostatique ? 2.6. En supposant que le potentiel est nul sur le plan chargé, déterminer V(M) en tout point de l'espace.   .

menu